代码

  1. import cv2, math
  2. import numpy as np
  3. import matplotlib.pyplot as plt
  4. ## 定义图像目录
  5. image_directory = 'D:\\Data_documents\\ImageProcess\\images\\'
  6. # 图像读取
  7. imgname = image_directory + 'lena.jpg'
  8. img = cv2.imread(imgname)
  10. # 图像显示在一个新的名字为'image'的窗口中，如果看不到，在任务栏中把窗口恢复后观察图像，在窗口中按任意键关闭窗口
  11. cv2.imshow('image',img)
  12. cv2.waitKey(0)
  13. cv2.destroyAllWindows()

计算计算Fourier变换

1.1 图像的2D DFFT直接显示

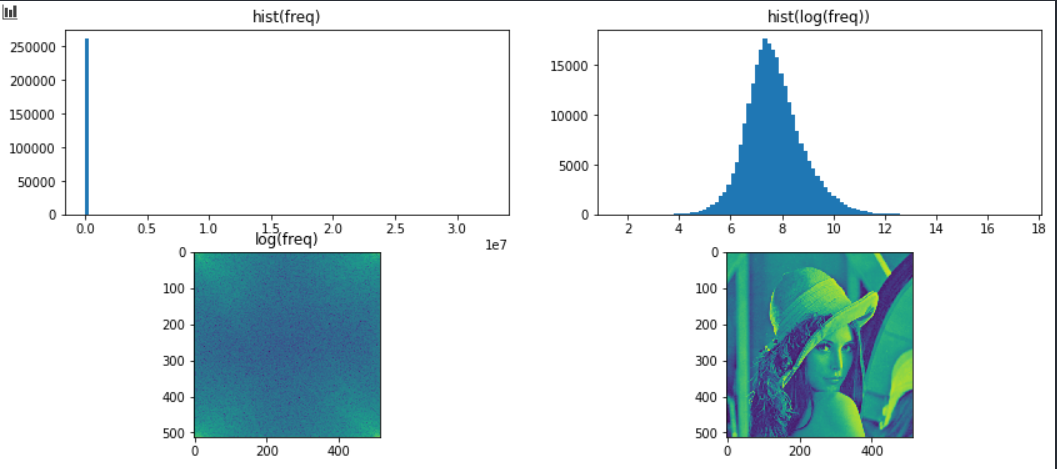
  1. # 计算Fourier变换
  2. # 彩色图像转化为灰度图像， 只有灰度图像才能计算Fourier变换
  3. grayimg = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)            
  4. f = np.fft.fft2(grayimg)
  6. # 先取幅值
  7. freq = np.abs(f)
  9. # 再显示一下Fourier变换结果的直方图看看
  10. fig, ax = plt.subplots(nrows=2, ncols=2, figsize=(14, 6))
  11. ax[0,0].hist(freq.ravel(), bins=100)
  12. ax[0,0].set_title('hist(freq)')
  14. # 观察：有一部分的数值非常大，其余的很小，看不到了
  16. ax[0,1].hist(np.log(freq).ravel(), bins=100)
  17. ax[0,1].set_title('hist(log(freq))')
  19. # 观察：取对数之后才能看到其它部分
  22. # 显示一下数据的二维分布，数值越大自动显示的颜色越亮
  23. ax[1,0].imshow(np.log(freq), interpolation="none")
  24. ax[1,0].set_title('log(freq)')
  26. #  观察：频谱图可以看到四个角比较亮，中间比较暗
  29. # 显示灰度图像
  30. ax[1,1].imshow(grayimg, interpolation="none")
  31. plt.show()
  33. #  观察：灰度图像 也按照灰度的大小用色彩显示出来，这是一种伪彩色显示图像的方法

image.png

1.2 图像的2D DFFT 偏移后能量集中的显示

  1. grayimg = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)            
  3. # 通常的 Fourier 2D 变换
  4. dft = np.fft.fft2(grayimg)
  5. fshift = np.fft.fftshift(dft)
  6. freq = np.log(np.abs(fshift))
  8. # 显示， 和上面类似，这里采用 cmap = 'gray' 参数 显示为灰度图像
  9. plt.subplot(121),plt.imshow(grayimg, cmap = 'gray')
  10. plt.title('Input Image'), plt.xticks([]), plt.yticks([])
  11. plt.subplot(122),plt.imshow( freq, cmap = 'gray')
  12. plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
  13. plt.show()
  15. #  观察：频谱图中间亮，体现能量集中的特点

image.png

1.3 图像的2D DFFT反变换

  1. # Fourier反变换
  2. ishift = np.fft.ifftshift(fshift)
  3. iimg = np.fft.ifft2(ishift)
  4. iimg = np.abs(iimg)
  6. #展示结果
  7. plt.subplot(131), plt.imshow(grayimg, 'gray'), plt.title('Original Image')
  8. plt.axis('off')
  9. plt.subplot(132), plt.imshow(freq, 'gray'), plt.title('Fourier Image')
  10. plt.axis('off')
  11. plt.subplot(133), plt.imshow(iimg, 'gray'), plt.title('Inverse Fourier Image')
  12. plt.axis('off')
  13. plt.show()

image.png

1.4 CV函数进行 2D DFFT计算

  1. # Fourier变换
  2. dft = cv2.dft(np.float32(grayimg), flags = cv2.DFT_COMPLEX_OUTPUT)
  4. # 将频谱低频从左上角移动至中心位置
  5. dftshift = np.fft.fftshift(dft)
  7. # 频谱图像双通道复数转换为0-255区间
  8. result = 20*np.log(cv2.magnitude(dftshift[:,:,0], dftshift[:,:,1]))
  10. # Fourier反变换
  11. ishift = np.fft.ifftshift(dftshift)
  12. iimg = cv2.idft(ishift)
  13. res2 = cv2.magnitude(iimg[:,:,0], iimg[:,:,1])
  15. #显示
  16. plt.subplot(131), plt.imshow(grayimg, 'gray'), plt.title('Original Image')
  17. plt.axis('off')
  18. plt.subplot(132), plt.imshow(result, 'gray'), plt.title('Fourier Image')
  19. plt.axis('off')
  20. plt.subplot(133), plt.imshow(res2, 'gray'), plt.title('Inverse Fourier Image')
  21. plt.axis('off')
  22. plt.show()

图像的频域处理

2.1 低频观察

  1. grayimg = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)            
  3. # 通常的 Fourier 2D 变换
  4. dft = np.fft.fft2(grayimg)
  5. fshift = np.fft.fftshift(dft)
  6. freq = np.log(1+np.abs(fshift))
  8. # 去掉矩形框之外的数据(置0)
  9. freq_center = fshift[256-32:256+32,256-32:256+32].copy()
  10. fshift2 = np.zeros([fshift.shape[0],fshift.shape[1]] ,dtype = np.complex64)
  11. fshift2[256-32:256+32,256-32:256+32] = freq_center
  12. freq2 = np.log(1+np.abs(fshift2))
  14. # Fourier反变换
  15. ishift3 = np.fft.ifftshift(fshift2)
  16. iimg = np.fft.ifft2(ishift3)
  17. iimg = np.abs(iimg)
  19. #展示结果
  20. plt.subplot(221), plt.imshow(grayimg, 'gray'), plt.title('Original')
  21. plt.axis('off')
  22. plt.subplot(222), plt.imshow(freq, 'gray'), plt.title('Fourier1')
  23. plt.axis('off')
  24. plt.subplot(223), plt.imshow(freq2, 'gray'), plt.title('Fourier2')
  25. plt.axis('off')
  26. plt.subplot(224), plt.imshow(iimg, 'gray'), plt.title('New Image')
  27. plt.axis('off')
  28. plt.show()

image.png

2.2 高频观察

  1. grayimg = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)            
  3. # 通常的 Fourier 2D 变换
  4. dft = np.fft.fft2(grayimg)
  5. fshift = np.fft.fftshift(dft)
  6. freq = np.log(1+np.abs(fshift))
  8. # 去掉矩形框之内的数据(置0)
  9. fshift2 = fshift.copy()
  10. fshift2[256-32:256+32,256-32:256+32] = 0
  11. freq2 = np.log(1+np.abs(fshift2))
  13. # Fourier反变换
  14. ishift3 = np.fft.ifftshift(fshift2)
  15. iimg = np.fft.ifft2(ishift3)
  16. iimg = np.abs(iimg)
  18. #展示结果
  19. plt.subplot(221), plt.imshow(grayimg, 'gray'), plt.title('Original')
  20. plt.axis('off')
  21. plt.subplot(222), plt.imshow(freq, 'gray'), plt.title('Fourier1')
  22. plt.axis('off')
  23. plt.subplot(223), plt.imshow(freq2, 'gray'), plt.title('Fourier2')
  24. plt.axis('off')
  25. plt.subplot(224), plt.imshow(iimg, 'gray'), plt.title('New Image')
  26. plt.axis('off')
  27. plt.show()

image.png

2.3 观察一个算子是低频滤波还是高频滤波

  1. # simple averaging filter without scaling parameter
  2. mean_filter = np.ones((3,3))
  4. # creating a guassian filter
  5. x = cv2.getGaussianKernel(5,10)
  6. #x.T 为矩阵转置
  7. gaussian = x*x.T
  9. # different edge detecting filters
  10. # scharr in x-direction
  11. scharr = np.array([[-3, 0, 3],
  12.                    [-10,0,10],
  13.                    [-3, 0, 3]])
  14. # sobel in x direction
  15. sobel_x= np.array([[-1, 0, 1],
  16.                   [-2, 0, 2],
  17.                   [-1, 0, 1]])
  18. # sobel in y direction
  19. sobel_y= np.array([[-1,-2,-1],
  20.                    [0, 0, 0],
  21.                    [1, 2, 1]])
  22. # laplacian
  23. laplacian=np.array([[0, 1, 0],
  24.                     [1,-4, 1],
  25.                     [0, 1, 0]])
  28. filters = [mean_filter, gaussian, laplacian, sobel_x, sobel_y, scharr]
  29. filter_name = ['mean_filter', 'gaussian','laplacian', 'sobel_x', 'sobel_y', 'scharr_x']
  30. fft_filters = [np.fft.fft2(x) for x in filters]
  31. fft_shift = [np.fft.fftshift(y) for y in fft_filters]
  32. mag_spectrum = [np.log(np.abs(z)+1) for z in fft_shift]
  34. for i in range(6):
  35.     plt.subplot(2,3,i+1),plt.imshow(mag_spectrum[i],cmap = 'gray')
  36.     plt.title(filter_name[i]), plt.xticks([]), plt.yticks([])
  37. plt.show()
  39. # 观察亮的区域在图像的高频位置(外侧) ，还是低频位置 (中心)，对应能通过信号的区域

image.png

知识点

4.1 Fourier变换

4.2 DFT的计算与可视化

4.3 频域滤波

课件

机器视觉-第4章-频域图像增强.pdf