开发 gi 的时候，要用到一些图算法，唤起了多年前那段尘封的记忆，重温了胡凡的《算法笔记》。

Dijkstra

Dijkstra(中文译为戴克斯特拉算法) 是由荷兰计算机科学家艾兹赫尔·戴克斯特拉在1956年发现的算法。Dijkstra 算法用来解决单源最短路径问题，即给定图 G 和起点 start，通过算法得到 start 节点到其他每个节点的最短距离。
该过程可用下图来模拟。

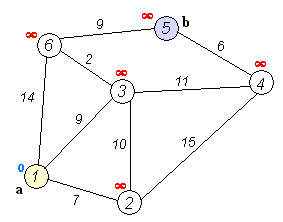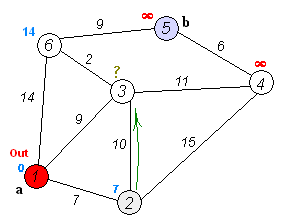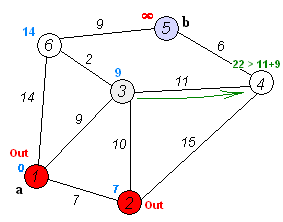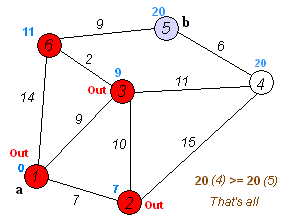
Dijkstra_Animation.gif

具体的算法思想可用参考胡凡的《算法笔记》 P369。

感兴趣的大哥麻烦自己找找 pdf，我只有纸质书。

Javascript 实现
来自 antv 旗下的 algorithm 库 ，https://github.com/antvis/algorithm/blob/master/packages/graph/src/dijkstra.ts
值得一提的是，在 G6 中的图既不是用邻接表也不是用邻接矩阵，而是采用了如下结果

  1. interface IGraph {
  2.   nodes: any[];
  3.   edges: any[];
  4. }

具体算法如下：

  1. const minVertex = (
  2.   D: { [key: string]: number },
  3.   nodes: NodeConfig[],
  4.   marks: { [key: string]: boolean },
  5. ): NodeConfig => {
  6.   // 找出最小的点
  7.   let minDis = Infinity;
  8.   let minNode;
  9.   for (let i = 0; i < nodes.length; i++) {
  10.     const nodeId = nodes[i].id;
  11.     if (!marks[nodeId] && D[nodeId] <= minDis) {
  12.       minDis = D[nodeId];
  13.       minNode = nodes[i];
  14.     }
  15.   }
  16.   return minNode;
  17. };
  19. const dijkstra = (
  20.   graphData: GraphData,
  21.   source: string,
  22.   directed?: boolean,
  23.   weightPropertyName?: string,
  24. ) => {
  25.   const { nodes = [], edges = [] } = graphData;
  26.   const nodeIds = [];
  27.   const marks = {};
  28.   const D = {};
  29.   const prevs = {}; // key: 顶点, value: 顶点的前驱点数组（可能有多条等长的最短路径）
  30.   nodes.forEach((node, i) => {
  31.     const id = node.id;
  32.     nodeIds.push(id);
  33.     D[id] = Infinity;
  34.     if (id === source) D[id] = 0;
  35.   });
  37.   const nodeNum = nodes.length;
  38.   for (let i = 0; i < nodeNum; i++) {
  39.     // Process the vertices
  40.     const minNode = minVertex(D, nodes, marks);
  41.     const minNodeId = minNode.id;
  42.     marks[minNodeId] = true;
  44.     if (D[minNodeId] === Infinity) continue; // Unreachable vertices cannot be the intermediate point
  46.     let relatedEdges: EdgeConfig[] = [];
  47.     if (directed) relatedEdges = getOutEdgesNodeId(minNodeId, edges);
  48.     else relatedEdges = getEdgesByNodeId(minNodeId, edges);
  50.     relatedEdges.forEach(edge => {
  51.       const edgeTarget = edge.target;
  52.       const edgeSource = edge.source;
  53.       const w = edgeTarget === minNodeId ? edgeSource : edgeTarget;
  54.       const weight = weightPropertyName && edge[weightPropertyName] ? edge[weightPropertyName] : 1;
  55.       if (D[w] > D[minNode.id] + weight) {
  56.         D[w] = D[minNode.id] + weight;
  57.         prevs[w] = [minNode.id];
  58.       } else if (D[w] === D[minNode.id] + weight) {
  59.         prevs[w].push(minNode.id);
  60.       }
  61.     });
  62.   }
  64.   prevs[source] = [source];
  65.   // 每个节点存可能存在多条最短路径
  66.   const paths = {};
  67.   for (const target in D) {
  68.     if (D[target] !== Infinity) {
  69.       findAllPaths(source, target, prevs, paths);
  70.     }
  71.   }
  73.   // 兼容之前单路径
  74.   const path = {};
  75.   for (const target in paths) {
  76.     path[target] = paths[target][0];
  77.   }
  78.   return { length: D, path, allPath: paths };
  79. };

c++ 实现
其中的图使用邻接表实现，参考了《算法笔记》的思路自己写了一般，摒弃了原书中 c+STL 的写法，改用 c++ 11 的新语法实现。

  1. #include <bits/stdc++.h>
  2. using namespace std;
  4. class Edge
  5. {
  6. public:
  7.     int to;
  8.     int cost;
  9.     Edge(int to, int cost)
  10.     {
  11.         this->to = to;
  12.         this->cost = cost;
  13.     }
  14. };
  16. void Dijkstra(int start, vector<vector<Edge>> graph)
  17. {
  18.     int n = graph.size();
  19.     // 距离
  20.     vector<int> dis(n, INT_MAX);
  21.     // 已经访问过的节点
  22.     vector<bool> visited(n, false);
  23.     dis[start] = 0;
  25.     for (int i = 0; i < n; i++)
  26.     {
  28.         // 寻找当前已知的最近节点
  29.         int nearestNode = -1;
  30.         int minDis = INT_MAX;
  31.         for (int j = 0; j <= n; j++)
  32.         {
  33.             if (!visited[j] && dis[j] < minDis)
  34.             {
  35.                 nearestNode = j;
  36.                 minDis = dis[j];
  37.             }
  38.         }
  40.         visited[nearestNode] = true;
  42.         for (Edge &edge : graph[nearestNode])
  43.         {
  44.             if (!visited[edge.to] && dis[nearestNode] + edge.cost < dis[edge.to])
  45.             {
  46.                 dis[edge.to] = dis[nearestNode] + edge.cost;
  47.             }
  48.         }
  49.     }
  50. }