数据结构和算法可以高效地解决性能问题，提高代码质量。从学科角度来说，算法也是计算机科学中基础的概念。

typescript 是 js 的超集，主要提供的功能是类型声明（类型检查、自动推断类型）、接口（泛型）。

数组

js 的第一个版本并没有数组，后面才实现的数组，可以保存多种类型，但是遵守最佳实践的话应该避免这么做。
使用数组可以保存一类信息，避免声明多个变量，写法上更简洁，还能利用数组的结构和方法进行更多便利的操作。

创建数组
字面量创建，构造函数创建，api 创建。

元素的增删改查
中括号加索引访问数组元素。
末尾添加元素，有两种方式，第一是中括号加索引添加，第二是用数组方法。nums[nums.length]=num;nums.push(num);nums.splice(nums.length,0,num);
头部添加元素，有两种方式，第一是中括号加索引，遍历数组，移项，for(let i = nums.length; i > 0; i--) nums[i] = nums[i-1]; nums[0] = num;。第二是用数组方法，nums.unshift(num)。
删除尾部元素，有两种方式，第一修改length，nums.length = nums.length - 1，第二是用数组方法，nums.pop()。
删除头部元素，有两种方式，第一是遍历数组，移项。第二是用数组方法，nums.shift()。
删除中间元素有两种方式，第一是遍历数组，移项，并改变 length。第二是数组方法，nums.splice(startIndex, deleteCounts)。

数组方法
image.png
迭代方法有every / filter / some / forEach / map / reduce / reduceRight。拼接字符串用join。
image.png
entries、keys、values 在集合、字典、散列表等数据结构中很有用。创建数组时from挺管用，fiil用来初始化也不错。查找元素可以用find / findIndex，查找元素的下标可以用indexOf / lastIndexOf，判断元素是否存在更好的方法是includes。
image.png
类型数组只能存放单一类型，声明语法是let array = new TypeArray(length)。类型数组在使用 webgl api、图像、文件、位操作时挺有用。

栈

栈是一种添加和删除元素有限制的线性表，只能在一端添加删除元素，这一端叫做栈顶，另一端叫栈底。栈遵守先进后出的原则。栈的应用非常多，涉及编译的地方都会用到栈，浏览器的历史记录也用的栈结构。js 中栈的实现有两种，基于数组和基于对象的。栈的方法有push / pop / peek / isEmpty / size / clear。

  1. // const _items = Symbol('items');
  2. const _items = new WeakMap();
  3. class Stack {
  4.     constructor() {
  5.         // this.items = [];
  6.         // this[_items] = [];
  7.         _items.set(this, []);
  8.     }
  9.     push(...elements) {
  10.         // elements.forEach(element => this.items.push(element));
  11.         // elements.forEach(element => this[_items].push(element));
  12.         elements.forEach(element => _items.get(this).push(element));
  13.         return this;
  14.     }
  15.     pop() {
  16.         // return this.items.pop();
  17.         // return this[_items].pop();
  18.         return _items.get(this).pop();
  19.     }
  20.     peek() {
  21.         // return this.items[this.items.length - 1];
  22.         // return this[_items][this[_items].length - 1];
  23.         return _items.get(this)[_items.get(this).length - 1];
  24.     }
  25.     size() {
  26.         // return this.items.length;
  27.         // return this[_items].length;
  28.         return _items.get(this).length;
  29.     }
  30.     isEmpty() {
  31.         // return this.items.length === 0;
  32.         // return this[_items].length === 0;
  33.         return _items.get(this).length === 0;
  34.     }
  35.     clear() {
  36.         // this.items = [];
  37.         // this[_items] = [];
  38.         _items.set(this, []);
  39.     }
  40. }
  42. class StackByObject {
  43.     constructor() {
  44.         this.count = 0; // 需要一个变量记录栈的大小
  45.         this.items = {};
  46.     }
  47.     push(element) {
  48.         this.items[this.count] = element;
  49.         this.count++;
  50.         return this;
  51.     }
  52.     pop() {
  53.         if (this.isEmpty()) return ;
  54.         this.count--;
  55.         const result = this.items[this.count];
  56.         delete this.items[this.count];
  57.         return result;
  58.     }
  59.     isEmpty() {
  60.         return this.count === 0;
  61.     }
  62.     size() {
  63.         return this.count;
  64.     }
  65.     peek() {
  66.         if (this.isEmpty()) return;
  67.         return this.items[this.count - 1];
  68.     }
  69.     clear() {
  70.         this.items = {};
  71.         this.count = 0;
  72.     }
  73.     toString() { // 基于对象的栈需要子实现 toString 方法。
  74.         if (this.isEmpty()) return '';
  75.         let ret = `${this.items[0]}`;
  76.         for (let i = 1; i < this.count; i++) {
  77.             ret += `,${this.items[i]}`;
  78.         }
  79.         return ret;
  80.     }
  81. }
  83. export { Stack, StackByObject };
  1. 私有属性有两种方案，symbol、weakMap。symbol 的话还不算真正的私有，有 Object.getOwnPropertySymbols 方法可以获取对象的 Symbol 属性。weakMap 倒是可以，但是代码可读性差，而且没法继承。<br />ts 的 private 属性在编译之后还是公开的。有个提案在类中使用 # 表示私有属性。

队列

递归

递归是解决问题的一种方法，将大问题拆分为相同逻辑的子问题，先从各个子问题开始解决，最后就可以解决最初的问题。递归的实现形式就是函数调用自身，包含直接调用和间接调用。
什么叫间接调用？就是有两个函数，在函数内部调用另一个函数。

递归函数最重要的是需要终止条件，否则递归将循环的执行下去，或者直到栈溢出错误。

js 中虽然提出了尾调用优化的技术，但是真正实现这一技术的浏览器很少。

有两个例子非常经典，阶乘和斐波那契数列。在斐波那契数列中还可以使用记忆化技术。

记忆化技术相当于一种缓存，也是利用空间换时间，防止递归函数重复的计算相同的值。

树

树是一种非线性的数据结构，在存储需要快速查找的数据时非常有用。
外部节点就是叶节点。
节点的深度取决于祖先节点的个数。
树的高度取决于最大的节点深度。
BST树
这一章节主要讲BST、ALV、红黑树。首先，如何创建BST类，然后实现其他方法，insert(key) / search(key) / inOrderTraverse() / preOrderTraverse() / postOrderTraverse() / min() / max() / remove(key)。
insert(key) 方法，首先要考虑树的根节点是否为空。第二步，将节点添加到根节点以外的位置，这时候就需要一个辅助方法 insertNode(node, key)，这个方法是递归的，回去遍历子树，直到找到合适的位置。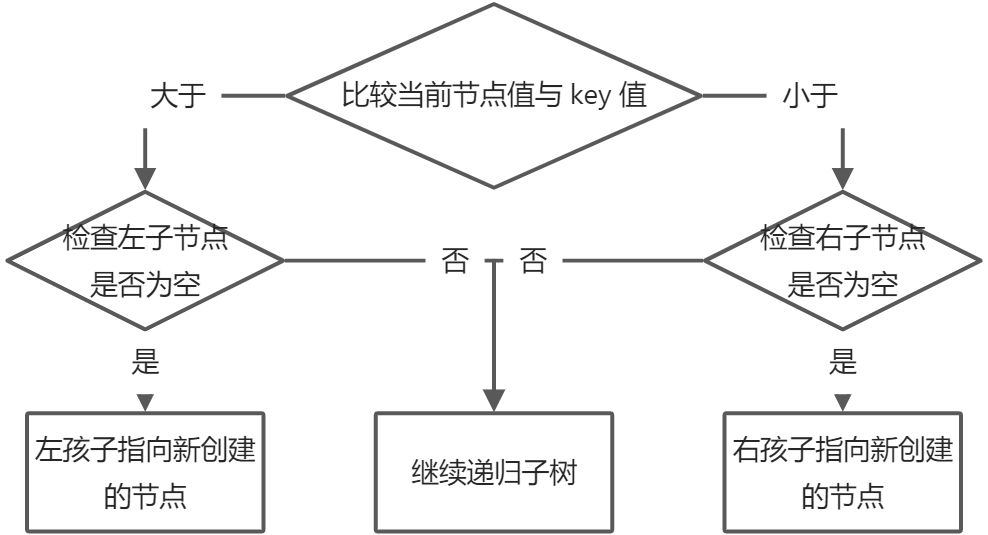
《学习js数据结构与算法》 - 图4

树的遍历有3种方法，前序、中序、后序。书中的实现是传入一个回调函数，对每个节点执行这个回调。这种模式叫做“访问者模式”，这种模式 js 中不是常用嘛，在数组的遍历方法中。
前序的遍历顺序是节点本身、左孩子、右孩子。中序是左孩子、节点本身、右孩子。后序是左、右、节点本身。前序遍历有一个应用是打印结构化的文档，后序遍历是计算一个目录及其子目录中所有文件所占空间的大小。

BST 的搜索操作主要有3种，查找特定值、找最小值、找最大值。后两者都比较简单，就是中序遍历的第一个和最后一个节点的值。二找特定的值就需要进行判断，进行一个二分的递归查找。

移除操作是最麻烦的，需要处理的场景很多，有的可能需要查找并调整节点的位置。书中的实现，实现了一个辅助方法 removeNode(node, key)，返回值是节点，终止条件是 node 为空。首先是找到要删除的节点，找到后需要处理3种情况，该节点是一个叶子节点，该节点只有一侧有子节点，该节点有两个子节点。
前两种情况很简单，叶子节点置空，有一个子节点的话就将这个节点返回，复杂的是两个子节点的情况，首先要找到节点右子树中最小的节点，用这个最小节点的值替换当前节点的值，然后将最小节点移除，最后返回当前节点。

AVL树
BST树存在一个问题，可能会随着插入的节点越多，导致树的某条边特别深。这在搜索、移除、添加操作时容易引起一些性能问题。AVL树是一种自平衡二叉搜索树，任何一个节点的左右子树高度之差最多为1。主要是在添加和移除节点的时候会通过旋转操作来保持平衡。
avl 树每个节点都有一个平衡因子，这个平衡因子其实就是左右子树的高度差。除了平衡因子，还有LL、RR、LR、RR，4种旋转，这个名字符号并不是旋转的方向，而是需要旋转出现的情况，比如LL是左子树深，需要右旋转，LR是左子树的右侧太深，需要先右旋再左旋。

红黑树
在 avl 的基础上，理解差异和改进。