从本案例中有助于理解动态规划中的重叠子问题和最优子结构。

    题目：

    给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。 返回你可以获得的最大乘积。

    示例 1:

    输入: 2 输出: 1 解释: 2 = 1 + 1, 1 × 1 = 1。

    示例 2:

    输入: 10 输出: 36 解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。

    思路分析

    这题先从暴力解法上入手，对数字不断分割，从1开始，直到 (n-1) 不能再分割为止。

    拿4这个数字来分析，分割如下：

    第一种情况，f(4) = 1 * f(3)，分割成 1 与 3 的乘积最大值
    继续分割3
    第一种情况，f(3) = 1 * f(2)，分割成1 与 2 的乘积最大值
    继续分割2
    f(2) = 1 * f(1)，分割成1与1的乘积最大值
    第二种情况，f(3) = 2 * (1)，分割成2与1的乘积最大值

    第二种情况，    f(4) = 2 f(2)，分割成 2 与 2 的乘积最大值
    继续分割2
    f(2) = 1     f(1)，分割成1与1的乘积最大值
    第二种情况，f(4) = 3 * f(1)，分割成 3 与 1 的乘积最大值
    1不能再分割了

    上述分析中，到1的时候便停止分割，1不能分割成别的数了。

    通过示意图来看分析过程，实际上就是一棵树的结构：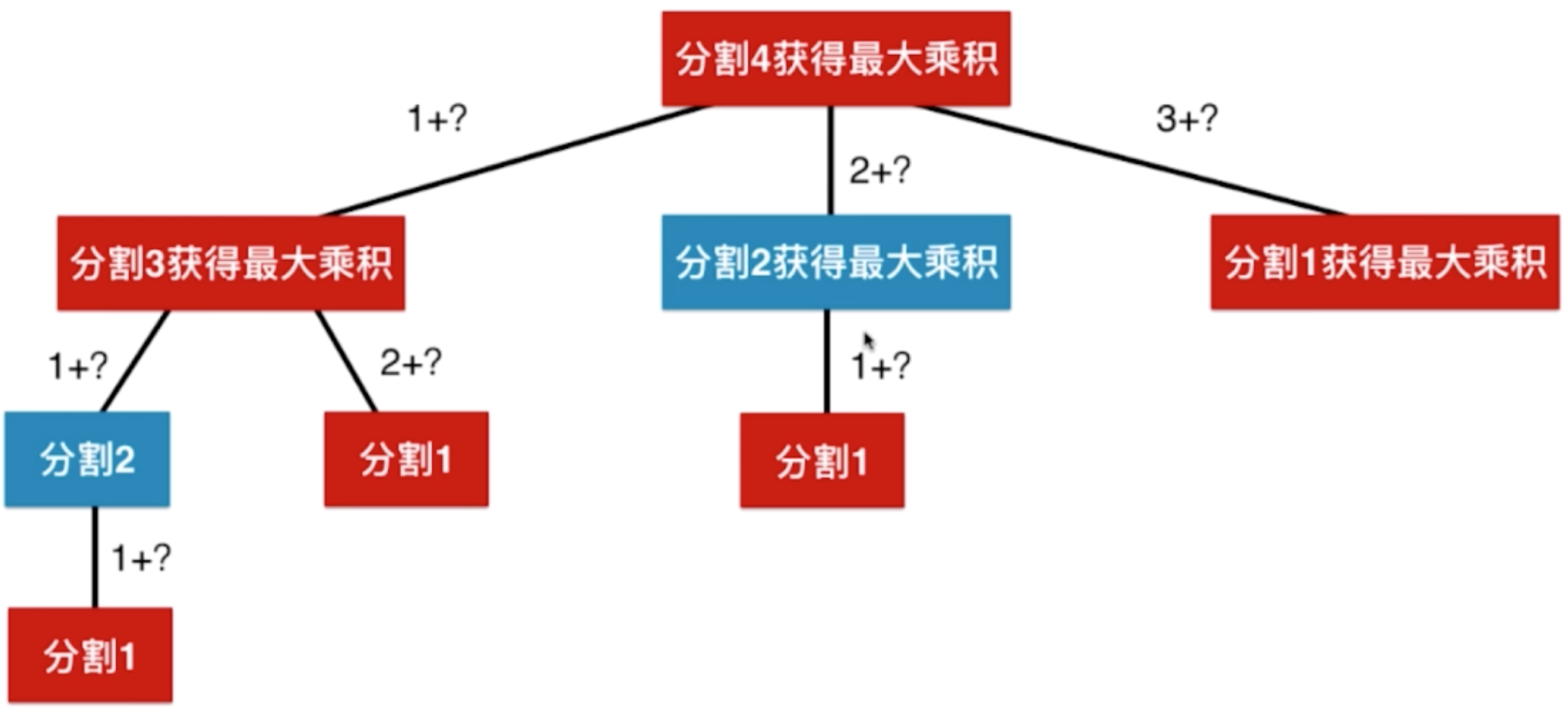
    image.png

    如果是 n 的数，则把 4 替换成 n 即可：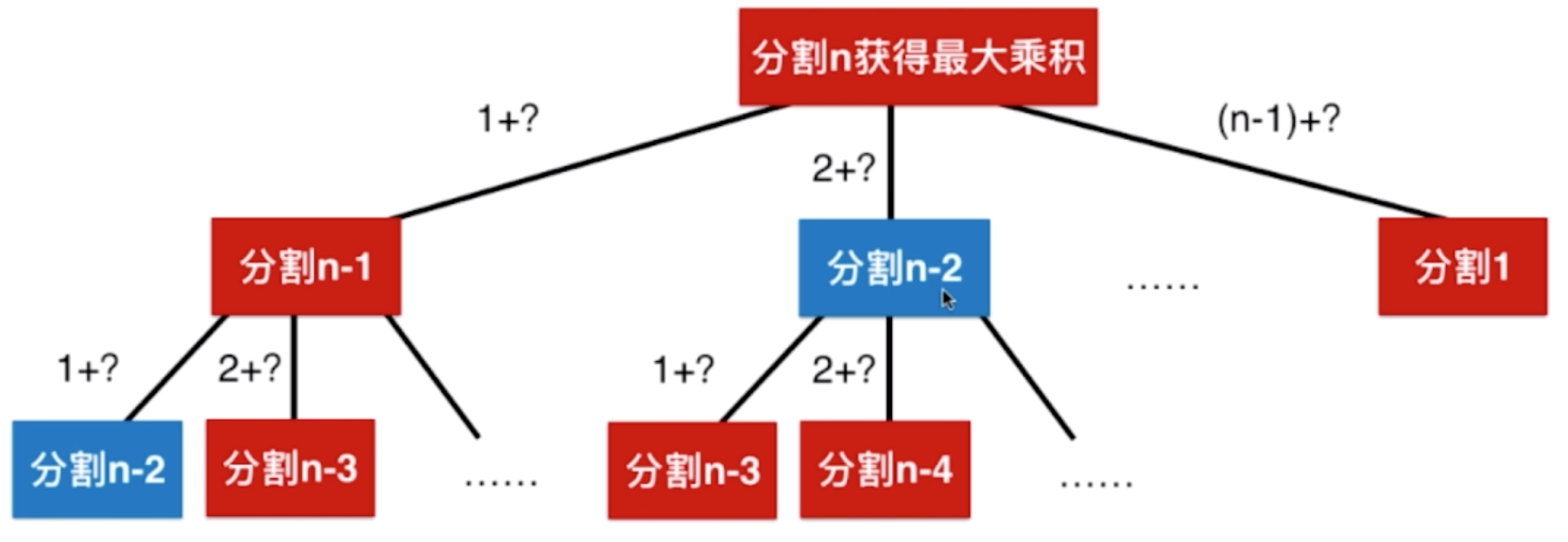
    image.png
    **
    通过画成树形结构可以清晰的看到拆分过程。

    解题可以选择自上而下的递归思路，把大问题拆分成一个个小问题，枚举每一种可能性。其中标记为蓝色的部分的块在重复计算，归为 重叠子问题 ，可采用「备忘录」（记忆化搜索）把算好的结果缓存起来直接使用。

    代码如下：

    1. /**
    2.  * @param {number} n
    3.  * @return {number}
    4.  */
    5. var integerBreak = function(n) {
    6.   if(n === 1) return 1
    7.   let cache = {}
    8.   // 对整数n进行分割两个数，求获得的最大乘积
    9.   const loop = (n) => {
    10.     if(n === 1) return 1;
    11.     // 如果已求值，则直接返回
    12.     if(cache[n]) return cache[n]
    13.     // 结果
    14.     let res = -1
    15.     for(let i = 1; i <= n - 1; i++){
    16.       // 找最大值
    17.       res = Math.max(res, i * (n - i), i * loop(n - i))
    18.     }
    19.     // 计算后，缓存起来
    20.     cache[n] = res
    22.     return res
    23.   }
    24.   return loop(n)
    25. };

    通过上面的代码，还有所画的树形示意图，每次递归调用函数进行循环，循环是树中每一层的拆分，从每一层中找到乘积最大值，就可以找到最终为的乘积最大值。
    值得注意是这段代码：

    res = Math.max(res, i * (n - i), i * loop(n - i))

    为什么是三个值比较呢？

    res 是存的最大值，在循环过程中不断要去和其他值比较，从而再次确定最大值，直到循环结束。
    i * (n - i) 是每次分割成两个数的乘积，在题目要求中是可以分割成两个数的，所以不能忽视分割成两数的乘积
    i * loop(n - i) 分割成 n-i 这个节点的乘积。

    动态规划实现

    通过上述的分析和代码可以看出，不断的拆分成子问题，然后在这些子问题中找到最优解，通过找到子问题的最优解，也就解决了原问题的最优解。并且包含着重叠子问题，我们可以采用动态规划自下而上的方式实现，只用循环不用递归。

    思路就是从1开始，不断的趋向求n的值，在这个过程中，不断的对其中的数字进行拆分.

    代码

    var integerBreak = function(n) {
  if(n === 1) return 1
  let cache = {}

  cache[1] = 1  // 
  // 求出从 1 → n 之间每个数的结果
  for(let i = 2; i <= n; i++){
    // 求解 i 的值
    // 把 i 进行从 1 到 i-1 的分割
    for(let j = 1; j <= i - 1; j++){
      // 分割成两部分 j + ( i - j )
      cache[i] = Math.max( cache[i] || -1, j * (i-j), j * cache[i-j])
    }

  }
  return cache[n]
}

    cache 是存储从 1 - n 之间每个数字求出来的结果。
    1 的结果就是1 ，不需要计算；循环从2开始。

    第一层循环 i 拿到 1 - n 之间的每一个数字，例如4，拿到的就是 2，3， 4。求出每一个数字的结果。
    第二层循环用来拆分每一个数字，从 1 开始，到 i - 1 ,例如 i 循环到的数字是3时，要拆分为 1，2。

    未完待续….