地址：https://leetcode-cn.com/problems/combination-sum/

题目描述：**

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取，也就是说选取过了，还可以继续选取。

示例：

  1. 输入：candidates = [2,3,6,7], target = 7,
  2. 所求解集为：
  3. [
  4.   [7],
  5.   [2,2,3]
  6. ]
  1. 输入：candidates = [2,3,5], target = 8,
  2. 所求解集为：
  3. [
  4.   [2,2,2,2],
  5.   [2,3,3],
  6.   [3,5]
  7. ]

利用回溯的思路，是一种笨办法，遍历所有情况找出问题的解。

回溯的思路

用回溯算法解决问题的一般步骤：

  • 针对所给问题，定义问题的解空间，它至少包含问题的一个（最优）解。
  • 确定易于搜索的解空间结构,使得能用回溯法方便地搜索整个解空间 。
  • 以深度优先的方式搜索解空间，并且在搜索过程中用剪枝函数避免无效搜索。

解决一个回溯问题，实际上就是一个决策树的遍历过程：

  • 路径：已经做出的选择
  • 选择列表：当前可以做的选择
  • 结束条件：已到决策树底层，无法再做选择了

搜索思路：

先画一个遍历的递归树：

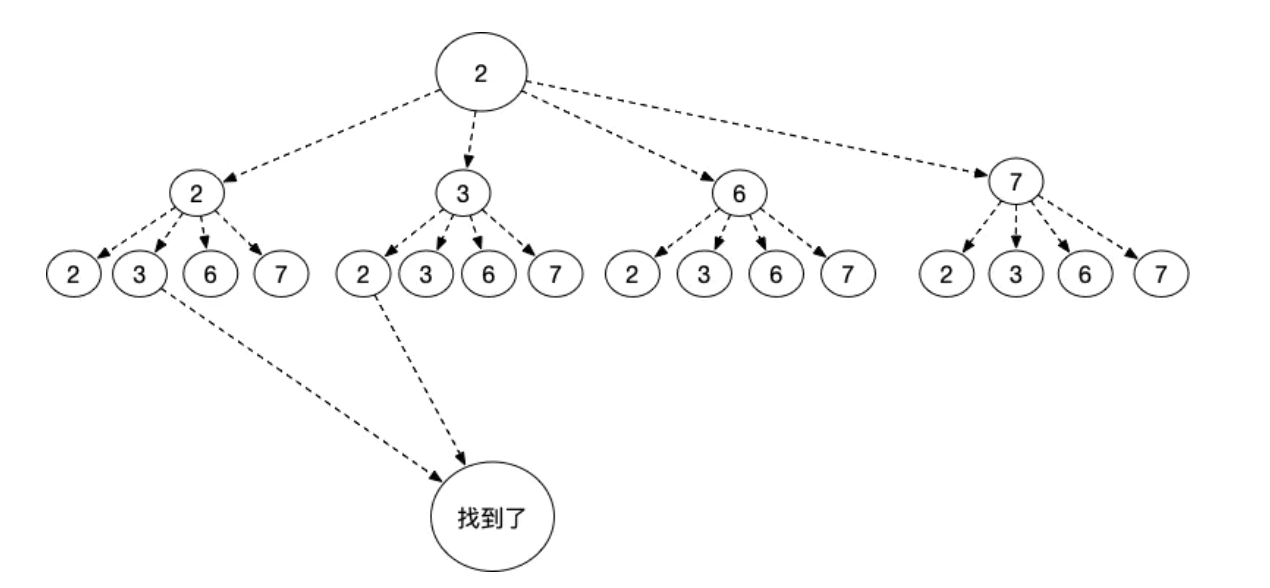
image.png

利用递归的方式，每一次递归调用函数，都会是树的一层元素，不断的选择路径，直到不满足条件，递归函数结束，再回溯到上一层树，继续选择路径。

题中要求可以同一个数字重复选取无限次，对同一个数字也要递归选取上。假如每次从数组开始循环时，会出现重复的结果集，这不符合题意，所以可以优化为 从上一层开始的位置向后选择

优化后的递归树：

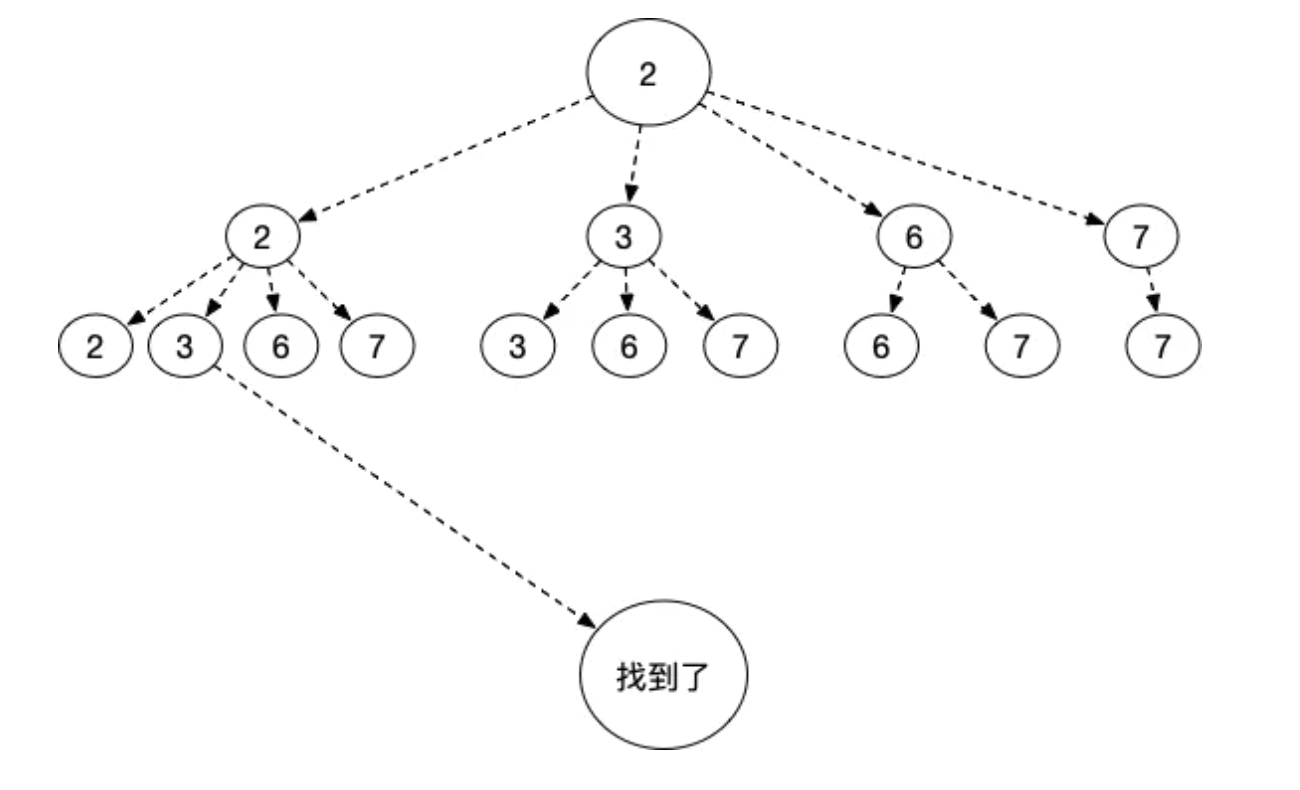
image.png

可以看出下一层开始位置，是上一层元素的位置，这样有效避免又选了之前的元素，造成结果集重复。

代码实现思路：

选择的路径

一般解题思路是，定义一个临时的数组，存储选择过的列表。循环开始时，把该路径的元素存入数组，递归结束，回溯回来，从列表中弹出，继续进行下一轮的选择。

每次选择，要判断选择的路径中元素之和正好和 target 相同，则选择的路径符合要求，存入到结果集中。

结束条件

本题的结束条件为选择的路径的元素之和，大于了 target，则说明不符合条件，本次选择路径结束，停止递归。

示例代码：

  1. /**
  2.  * @param {number[]} candidates
  3.  * @param {number} target
  4.  * @return {number[][]}
  5.  */
  6. var combinationSum = function(candidates, target) {
  8.   const len = candidates.length;
  9.   const child = []
  10.   const result = []
  12.   const loop = (index, sum) => {  // index 从哪里开始 sum 上次计算总和
  13.     // 和目标相同，则找到了一对组合
  14.     if(sum === target) {
  15.       result.push(child.slice())
  16.     }
  17.     // 组合相加结果大于目标了，则说明不符合
  18.     if(sum > target) {
  19.       return
  20.     }
  21.     // i 每次从 0 开始，则有重复的结果集
  22.     // i 从上一层的位置开始，则有效避免重复集
  23.     for(let i = index; i < len; i++){
  24.       child.push(candidates[i])
  25.       loop(i, sum + candidates[i] )
  26.       child.pop()
  27.     }
  28.   }
  30.   loop(0,0)
  32.   return result
  33. };
  35. console.log(combinationSum([2,3,6,7], 7)) // [ [ 2, 2, 3 ], [ 7 ] ]
  36. console.log(combinationSum([2,3,5], 8))  // [ [ 2, 2, 2, 2 ], [ 2, 3, 3 ], [ 3, 5 ] ]

总结：

本题和其他回溯的题目思路一致，只是在结束条件时稍微不同。通常结束条件是以到递归树的底层结束，本题是在大于 target 结束。

其他思路，待补充。。。。

参考：https://juejin.cn/post/6844903879826489358