1 简单回归问题

lesson3.pdf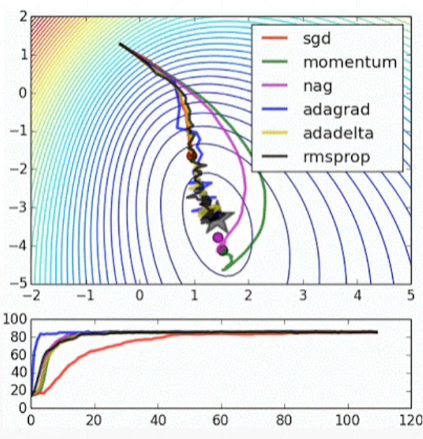
image.png
常用的也就sgd和rmsprop

可以精确求解的方程组称为 Closed Form Solution

实际数据可能有噪声项ch03 回归问题 1.42h - 图2
image.png

红色往低的蓝色走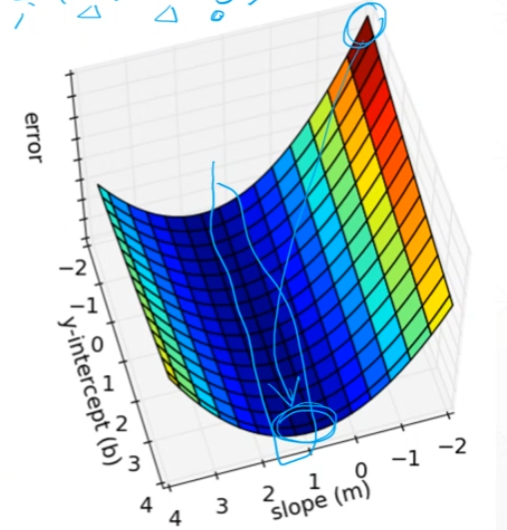
image.png

凸函数：Convex Optimization

2 回归问题实战

lesson4.pdf
data.csv
gd.py

  1. import numpy as np
  4. def compute_error_for_line_given_points(b, w, points):
  5.     """ 均方误差
  6.         y = wx + b
  7.     """
  8.     total_error, n = 0, len(points)
  9.     for i in range(n):
  10.         x, y = points[i]  # 这批数据数据是一维的x，标记也是一维的y
  11.         total_error += (y - (w * x + b)) ** 2
  12.     return total_error / n
  15. def step_gradient(b_current, w_current, points, learning_rate):
  16.     b_gradient, w_gradient = 0, 0
  17.     n = len(points)
  18.     for i in range(n):
  19.         x, y = points[i]
  20.         # 损失函数关于b、w的梯度
  21.         b_gradient += -(2 / n) * (y - ((w_current * x) + b_current))
  22.         w_gradient += -(2 / n) * x * (y - ((w_current * x) + b_current))
  23.     new_b = b_current - (learning_rate * b_gradient)
  24.     new_m = w_current - (learning_rate * w_gradient)
  25.     return new_b, new_m
  28. def gradient_descent_runner(points, starting_b, starting_w, learning_rate, num_iterations):
  29.     b, w = starting_b, starting_w
  30.     for i in range(num_iterations):
  31.         b, w = step_gradient(b, w, np.array(points), learning_rate)
  32.     return b, w
  35. def run():
  36.     points = np.genfromtxt("data.csv", delimiter=",")
  37.     learning_rate = 0.0001
  38.     initial_b = 0  # initial y-intercept guess
  39.     initial_m = 0  # initial slope guess
  40.     num_iterations = 1000
  41.     print("Starting gradient descent at b = {0}, m = {1}, error = {2}"
  42.           .format(initial_b, initial_m,
  43.                   compute_error_for_line_given_points(initial_b, initial_m, points))
  44.           )
  45.     print("Running...")
  46.     b, m = gradient_descent_runner(points, initial_b, initial_m, learning_rate, num_iterations)
  47.     print("After {0} iterations b = {1}, m = {2}, error = {3}".
  48.           format(num_iterations, b, m,
  49.                  compute_error_for_line_given_points(b, m, points))
  50.           )
  53. if __name__ == '__main__':
  54.     run()
  56. # 误差从5565降到112
  57. # Starting gradient descent at b = 0, m = 0, error = 5565.107834483211
  58. # Running...
  59. # After 1000 iterations b = 0.08893651993741346, m = 1.4777440851894448, error = 112.61481011613473

3 分类问题引入

lesson5.pdf

one-hot编码方式（也叫独热编码，又称为一位有效编码）
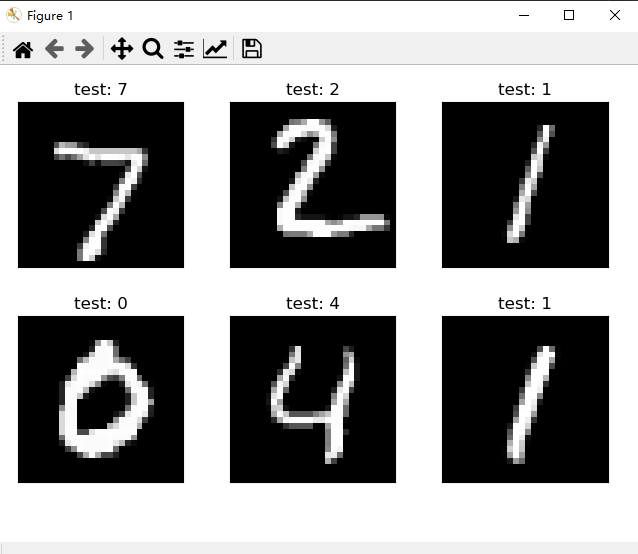
image.png

4 手写数字识别初体验

utils.py
mnist_train.py

import torch
from torch import nn
from torch.nn import functional as F
from torch import optim

import torchvision
from matplotlib import pyplot as plt

____util = """
"""


def plot_curve(data):
    fig = plt.figure()
    plt.plot(range(len(data)), data, color='blue')
    plt.legend(['value'], loc='upper right')
    plt.xlabel('step')
    plt.ylabel('value')
    plt.show()


def plot_image(img, label, name):
    fig = plt.figure()
    for i in range(6):
        plt.subplot(2, 3, i + 1)
        plt.tight_layout()
        plt.imshow(img[i][0] * 0.3081 + 0.1307, cmap='gray', interpolation='none')
        plt.title("{}: {}".format(name, label[i].item()))
        plt.xticks([])
        plt.yticks([])
    plt.show()


def one_hot(label, depth=10):
    out = torch.zeros(label.size(0), depth)  # .size(0)，获得第0维的大小
    idx = torch.LongTensor(label).view(-1, 1)
    out.scatter_(dim=1, index=idx, value=1)
    return out

Load data

torch.utils.data.DataLoader

____mnist_train = """
"""

# step1. load dataset
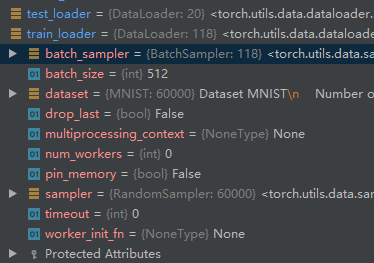
batch_size = 512

# 训练数据共6万张图（每张图28*28=784），每512张分为一个batch，共有118个batch
train_loader = torch.utils.data.DataLoader(
    torchvision.datasets.MNIST('mnist_data', train=True, download=True,
                               transform=torchvision.transforms.Compose([  # 数据处理
                                   torchvision.transforms.ToTensor(),  # np转tensor
                                   torchvision.transforms.Normalize(  # 标准化
                                       (0.1307,), (0.3081,))
                               ])),
    batch_size=batch_size, shuffle=True)

# 测试数据共1万张，分成20个batch
test_loader = torch.utils.data.DataLoader(
    torchvision.datasets.MNIST('mnist_data/', train=False, download=True,
                               transform=torchvision.transforms.Compose([
                                   torchvision.transforms.ToTensor(),
                                   torchvision.transforms.Normalize(
                                       (0.1307,), (0.3081,))
                               ])),
    batch_size=batch_size, shuffle=False)

image.png

plot_image

def plot_image(img, label, name):
    """查看6张图效果"""
    fig = plt.figure()
    for i in range(6):
        plt.subplot(2, 3, i + 1)
        plt.tight_layout()
        plt.imshow(img[i][0] * 0.3081 + 0.1307, cmap='gray', interpolation='none')
        plt.title("{}: {}".format(name, label[i].item()))
        plt.xticks([])
        plt.yticks([])
    plt.show()

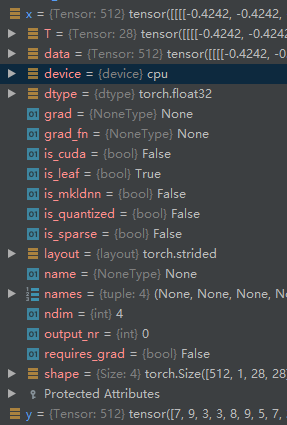
x, y = next(iter(train_loader))  # 获得一个batch的数据，x是数据特征，y是标记
print(x.shape, y.shape, x.min(), x.max())
# torch.Size([512, 1, 28, 28]) torch.Size([512]) tensor(-0.4242) tensor(2.8215)
# 如果去掉规范化，这里输出的最小最大值为：tensor(0.) tensor(1.)
plot_image(x, y, 'image sample')

image.png
image.png

Build Model

class Net(nn.Module):

    def __init__(self):
        super().__init__()

        # xw+b
        self.fc1 = nn.Linear(28 * 28, 256)
        self.fc2 = nn.Linear(256, 64)
        self.fc3 = nn.Linear(64, 10)

    def forward(self, x):
        # x: [b, 1, 28, 28]
        # h1 = relu(x*w1+b1)
        x = F.relu(self.fc1(x))
        # h2 = relu(h1*w2+b2)
        x = F.relu(self.fc2(x))
        # h3 = h2*w3+b3
        x = self.fc3(x)

        return x

Train

net = Net()
# [w1, b1, w2, b2, w3, b3]
optimizer = optim.SGD(net.parameters(), lr=0.01, momentum=0.9)

train_loss = []

for epoch in range(3):

    for batch_idx, (x, y) in enumerate(train_loader):

        # x: [b, 1, 28, 28], y: [512]
        # [b, 1, 28, 28] => [b, 784]
        x = x.view(x.size(0), 28 * 28)
        # => [b, 10]
        out = net(x)
        # [b, 10]
        y_onehot = one_hot(y)
        # loss = mse(out, y_onehot)
        loss = F.mse_loss(out, y_onehot)

        optimizer.zero_grad()  # 清零梯度
        loss.backward()
        # w' = w - lr*grad
        optimizer.step()

        train_loss.append(loss.item())

        if batch_idx % 10 == 0:
            print(epoch, batch_idx, loss.item())

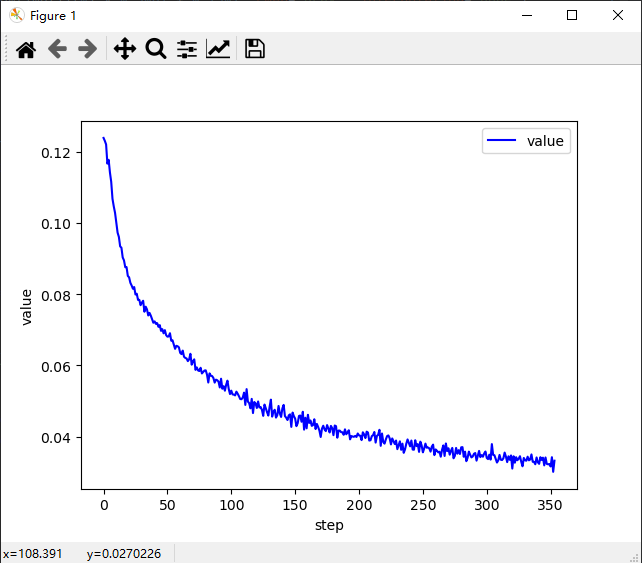
plot_curve(train_loss)
# we get optimal [w1, b1, w2, b2, w3, b3]

image.png

Test

total_correct = 0
for x, y in test_loader:
    x = x.view(x.size(0), 28 * 28)
    out = net(x)
    # out: [b, 10] => pred: [b]
    pred = out.argmax(dim=1)
    correct = pred.eq(y).sum().float().item()
    total_correct += correct

total_num = len(test_loader.dataset)
acc = total_correct / total_num
print('test acc:', acc)  # test acc: 0.8857

x, y = next(iter(test_loader))
out = net(x.view(x.size(0), 28 * 28))
pred = out.argmax(dim=1)
plot_image(x, pred, 'test')

image.png