线性支持向量机

介绍
超平面
我们如何找到最佳的超平面/直线？
如何最大化边距？
忽略异常值
核 SVM
总结
动机
代码示例
参考文献

原文： https://machine-learning-course.readthedocs.io/en/latest/content/supervised/linear_SVM.html

介绍

支持向量机（简称 SVM）是用于对数据进行分类的另一种机器学习算法。 SVM 的要点是尝试找到一条线或超平面来划分维空间，从而最好地对数据点进行分类。如果我们试图划分两个类 A 和 B，我们将尝试最好地用一条线将这两个类分开。线/超平面的一侧将是 A 类的数据，而另一侧将是 B 类的数据。这种分类法在分类中非常有用，因为我们必须一次计算最佳的线或超平面，并且任何新的数据点都可以轻松地计算出来。仅通过查看它们落在行的哪一侧即可对其进行分类。这与 k 最近邻算法相反，在 k 算法中，我们必须计算每个数据点最近的邻居。

超平面

超平面取决于它所在的空间，但是它将空间分成两个断开的部分。例如，一维空间将只是一个点，二维空间将是一条线，三维空间将是一个平面，依此类推。

我们如何找到最佳的超平面/直线？

您可能想知道可能会有多行将数据很好地拆分。实际上，可以划分两类的行数是无限的。正如您在下图中所看到的，每一行都将正方形和圆形分开，那么我们选择哪一个呢？

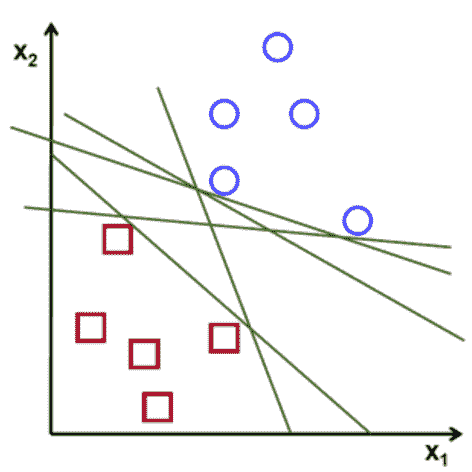
线性支持向量机 - 图1

参考： https://towardsdatascience.com/support-vector-machine-introduction-to-machine-learning-algorithms-934a444fca47

那么 SVM 如何找到将这两类分开的理想直线呢？它不仅是随机选择一个。该算法选择具有最大边距的线/超平面。最大化边距将为我们提供对数据进行分类的最佳行。如下图所示。

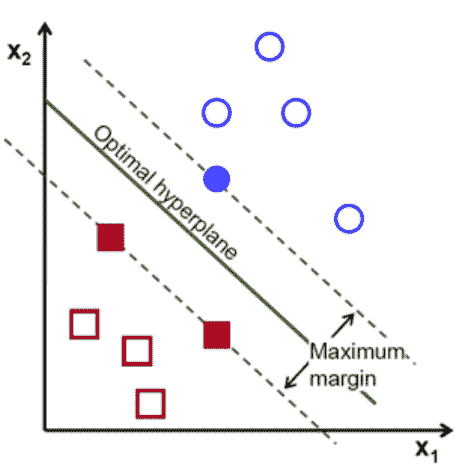
线性支持向量机 - 图2

参考： https://towardsdatascience.com/support-vector-machine-introduction-to-machine-learning-algorithms-934a444fca47

如何最大化边距？

最接近直线的数据是确定最佳直线的因素。这些数据点称为支持向量。它们显示为上方的正方形和圆形填充。这些向量到超平面的距离称为边距。通常，这些点离超平面越远，正确分类数据的可能性就越大。找到支持向量并最大化边距会涉及很多复杂的数学运算。我们不会去讨论；我们只想了解 SVM 背后的基本思想。

忽略异常值

有时，数据类将具有离群值。这些数据点与班级其余部分明显分开。支持向量机将忽略这些离群值。如下图所示。

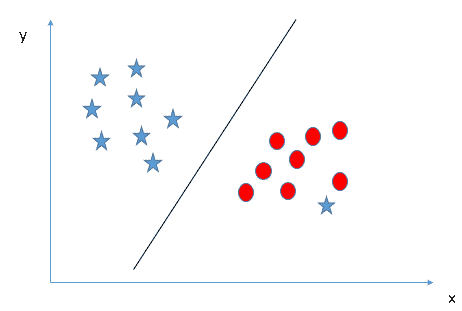
线性支持向量机 - 图3

参考： https://www.analyticsvidhya.com/blog/2017/09/understaing-support-vector-machine-example-code/

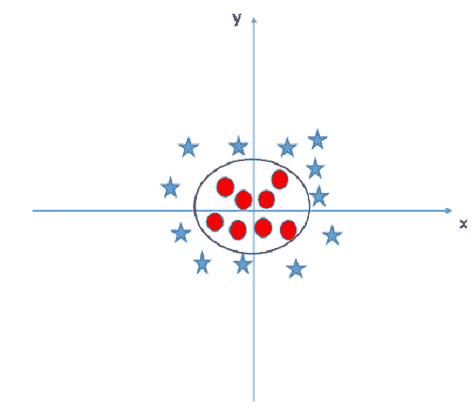
带有红色圆圈的星星是异常值。因此，SVM 将忽略异常值，并创建最佳行以将两个类分开。

核 SVM

会有无法用简单的线或超平面分开的数据类。这被称为非线性可分离数据。这是此类数据的示例。

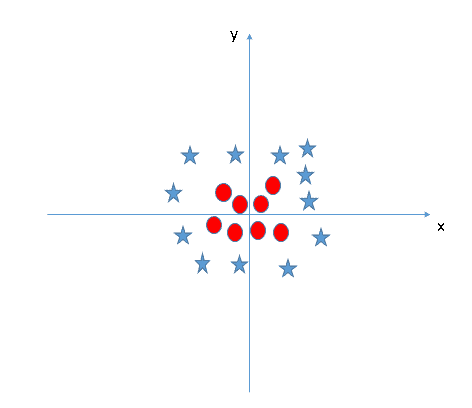
线性支持向量机 - 图4

参考： https://www.analyticsvidhya.com/blog/2017/09/understaing-support-vector-machine-example-code/

没有明确的方法将星星与圆圈分开。通过使用称为核技巧的技巧，SVM 将能够对非线性可分离数据进行分类。基本上，核技巧将点指向更高的维度，以将非线性可分离数据转换为线性可分离数据。因此，上图将用圆圈分隔，以分隔数据。

这是核技巧的一个示例。

线性支持向量机 - 图5

参考： https://www.analyticsvidhya.com/blog/2017/09/understaing-support-vector-machine-example-code/

有三种类型的核：

线性核
多项式核
径向基函数（RBF）核

您可以通过将“ model = svm.SVC（kernel =’linear’，C = 10000）”中的 kernel 值更改为“ poly”或“ rbf”来查看这些核如何改变最佳超平面的结果。这是在 linear_svm.py 中。

总结

SVM 是一种很好的机器学习技术，可以对数据进行分类。现在，我们对 SVM 有了一些了解，我们可以展示使用此分类器的优缺点。

SVM 的优点：

有效地对高维空间进行分类
节省内存空间，因为它仅使用支持向量来创建最佳行。
数据点可分离的最佳分类器

与 SVM 的缺点：

有大量数据集时效果不佳，训练时间更长。
当类重叠时，即不可分离的数据点，表现会很差。

动机

为什么要使用 SVM？可以对数据进行分类的模型很多。为什么要使用这个？如果您知道数据点很容易分离，那么这可能是最好的分类器。另外，可以使用核技巧来扩展它，因此请尝试使用不同的核，例如径向基函数（RBF）。

代码示例

请查看我们的代码 linear_svm.py ，以了解如何使用 Python 的 Scikit-learn 库实现线性 SVM。有关 Scikit-Learn 的更多信息，请在中找到。

linear_svm.py ，对从 Scikit-Learn 的数据集库加载的一组乳腺癌数据进行分类。该程序将获取数据并将其绘制在图形上，然后使用 SVM 创建超平面以分离数据。它还绕圈了确定超平面的支持向量。输出应如下所示：

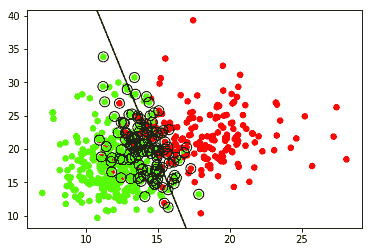
线性支持向量机 - 图6

绿点被分类为良性。红点归类为恶性。

这将从 Scikit-Learn 的数据集库中加载数据。您可以将数据更改为所需的任何数据。只要确保您拥有数据点和一系列目标即可对这些数据点进行分类。

dataCancer = load_breast_cancer()
data = dataCancer.data[:, :2]
target = dataCancer.target

您也可以将核更改为“ rbf”或“多项式”。这将创建一个不同的超平面来对数据进行分类。您可以在此处的代码中进行更改：

model = svm.SVC(kernel = 'linear', C = 10000)
model.fit(data, target)

介绍

超平面

我们如何找到最佳的超平面/直线？

如何最大化边距？

忽略异常值

核 SVM

总结

动机

代码示例

参考文献