原文: https://machine-learning-course.readthedocs.io/en/latest/content/supervised/decisiontrees.html
介绍
决策树是机器学习中的一个分类器,它使我们能够根据先前的数据进行预测。 它们就像一系列连续的“ if…then”语句,您将新数据馈入它们以获得结果。
为了演示决策树,让我们看一个例子。 想象一下,我们要预测麦克是否会在任何一天去杂货店购物。 我们可以看看导致 Mike 前往商店的先前因素:
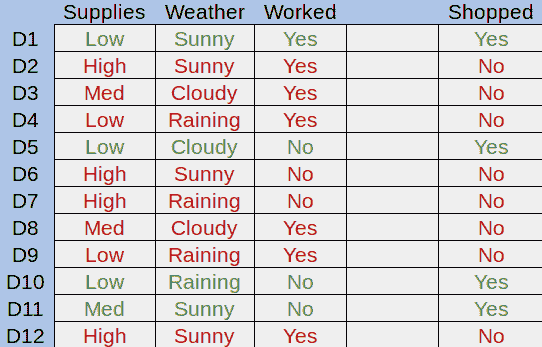
图 1.示例数据集
在这里,我们可以查看 Mike 的杂货供应量,天气以及 Mike 每天是否工作。 绿色的行是他去商店的日子,红色的行是他没有去的日子。 决策树的目标是尝试了解为什么 Mike 会去商店,然后将其应用于新数据。
让我们将第一个属性分成一棵树。 迈克的补给量可能少,中或大:
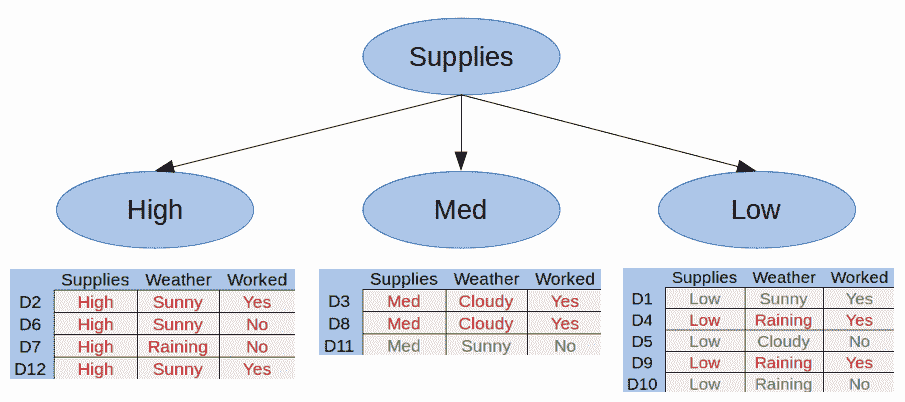
图 2.我们的第一个拆分
在这里,我们可以看到 Mike 的补给量很高,就永远不会去商店。 这称为纯子集,即仅包含正例或仅负例的子集。 使用决策树,无需进一步分解纯子集。
让我们将 Med Supplies 类别划分为 Mike 那天是否工作:
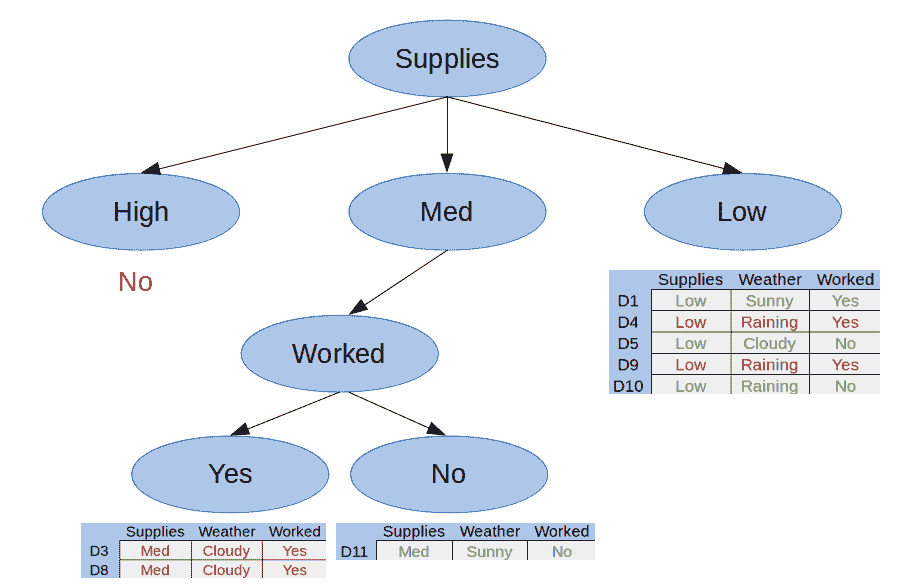
图 3.我们的第二个拆分
在这里我们可以看到我们还有两个纯子集,因此这棵树是完整的。 我们可以用它们各自的答案替换任何纯子集-在这种情况下,是或否。
最后,让我们按“天气”属性划分“供应不足”类别:
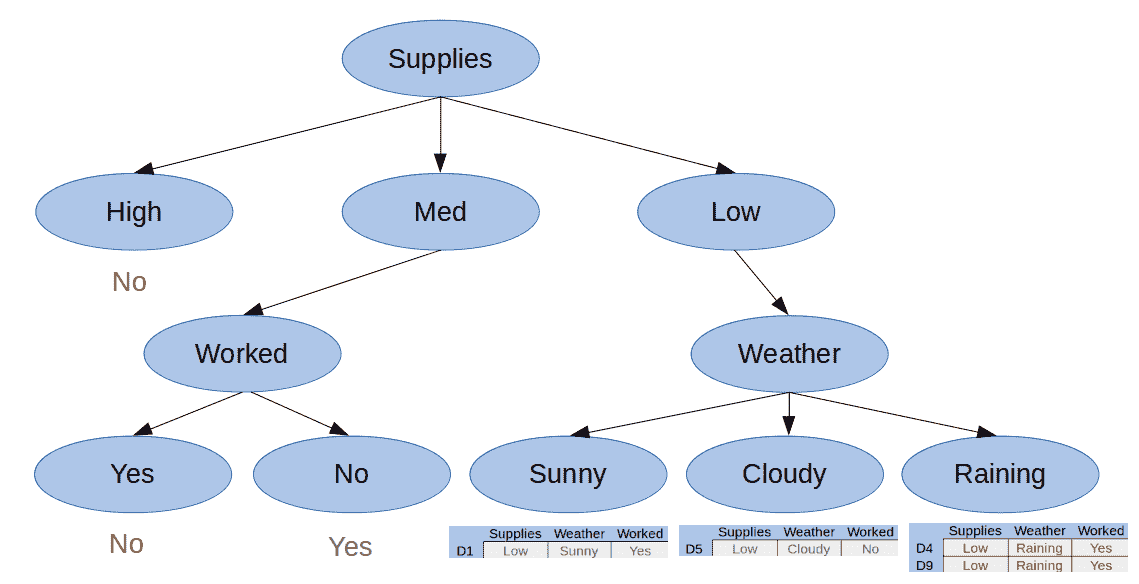
图 4.我们的第三个拆分
现在我们有了所有纯子集,我们可以创建最终决策树:
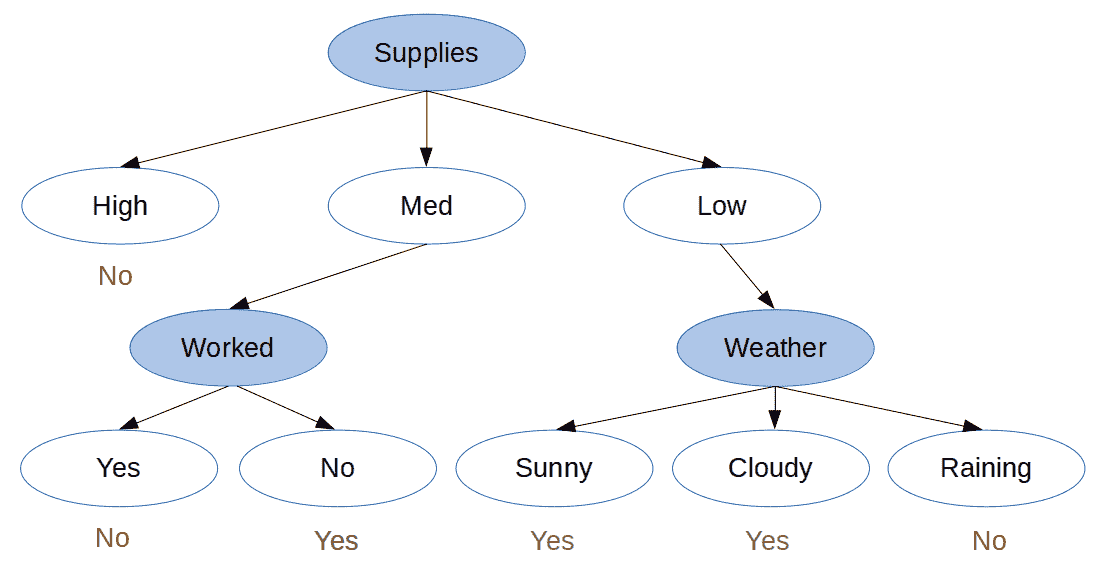
图 5.最终决策树
动机
决策树易于创建,可视化和解释。 因此,它们通常是用于对数据集建模的第一种方法。 决策树的层次结构和分类性质使其实现起来非常直观。 决策树根据您拥有的数据点数对数展开,这意味着较大的数据集对树的创建过程的影响将小于其他分类器。 由于树结构,对新数据点的分类也可以对数地执行。
分类和回归树
决策树算法也称为 CART 或分类和回归树。 与上面显示的树一样,分类树用于从一组可能的值中获取结果。 回归树是决策树,其中结果是连续值,例如汽车价格。
分裂(归纳)
决策树是通过称为归纳的拆分过程创建的,但是我们如何知道何时拆分? 我们需要一种递归算法,该算法确定要拆分的最佳属性。 一种这样的算法是贪婪算法:
- 从根开始,我们为每个属性创建一个拆分。
- 对于每个创建的拆分,请计算拆分成本。
- 选择成本最低的拆分。
- 递归到子树,然后从步骤 1 继续。
重复此过程,直到所有节点都具有与目标结果相同的值,或者拆分不会为预测增加任何值。 该算法将根节点作为最佳分类器。
分裂成本
分裂的成本由成本函数确定。 使用成本函数的目的是以一种可以计算的方式拆分数据,并提供最大的信息收益。
对于提供答案而不是提供值的分类树,我们可以使用基尼不纯度计算信息增益:
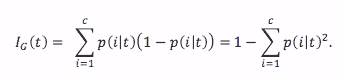
公式 1.基尼不纯度函数
Ref: https://sebastianraschka.com/faq/docs/decision-tree-binary.html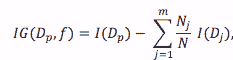
公式 2。基尼信息增益公式
Ref: https://sebastianraschka.com/faq/docs/decision-tree-binary.html
为了计算信息增益,我们首先开始计算根节点的基尼不纯度。 让我们看一下我们之前使用的数据:
| 供应量 | 天气 | 工作 | 购物? | |
|---|---|---|---|---|
| D1 | 低 | 晴 | 是 | 是 |
| D2 | 高 | 晴 | 是 | 否 |
| D3 | 中 | 多云 | 是 | 否 |
| D4 | 低 | 下雨 | 是 | 否 |
| D5 | 低 | 多云 | 否 | 是 |
| D6 | 高 | 晴 | 否 | 否 |
| D7 | 高 | 下雨 | 否 | 否 |
| D8 | 中 | 多云 | 是 | 否 |
| D9 | 低 | 下雨 | 是 | 否 |
| D10 | 低 | 下雨 | 否 | 是 |
| D11 | 中 | 晴 | 否 | 是 |
| D12 | 高 | 晴 | 是 | 否 |
我们的根节点是目标变量,无论迈克是否打算去购物。 要计算其基尼不纯度,我们需要找到每个结果的概率平方和,然后从一个结果中减去该结果:
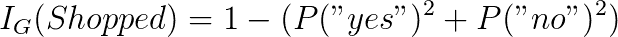
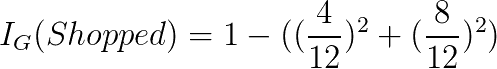

如果我们在第一个属性“供应量”上划分,我们来计算基尼信息增益。 我们可以分为三个不同的类别-低,中和高。 对于这些,我们计算其基尼不纯度:
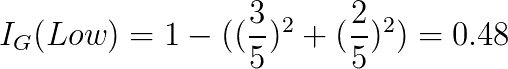
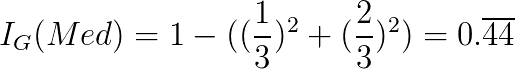

如您所见,高电源的不纯度为 0。这意味着如果我们分裂电源并接收高输入,我们将立即知道结果是什么。 为了确定此拆分的基尼信息增益,我们计算根的不纯度减去每个孩子的不纯度的加权平均值:
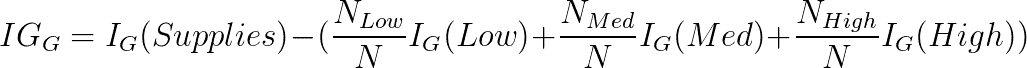
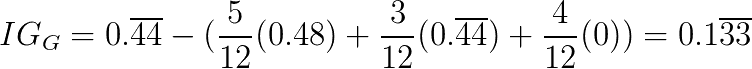
对于每个可能的分裂,我们都会继续使用此模式,然后选择能够为我们提供最高信息增益值的分裂。 最大化信息增益使我们可以进行最极化的分裂,从而降低了新输入被错误分类的可能性。
修剪
通过足够大的数据集创建的决策树最终可能会产生过多的拆分,每个拆分的有用性都会降低。 高度详细的决策树甚至可能导致过拟合,如上一模块中所述。 因此,删除决策树中不重要的部分是有益的。 修剪涉及计算每个结束子树(叶节点及其父节点)的信息增益,然后删除信息增益最小的子树:
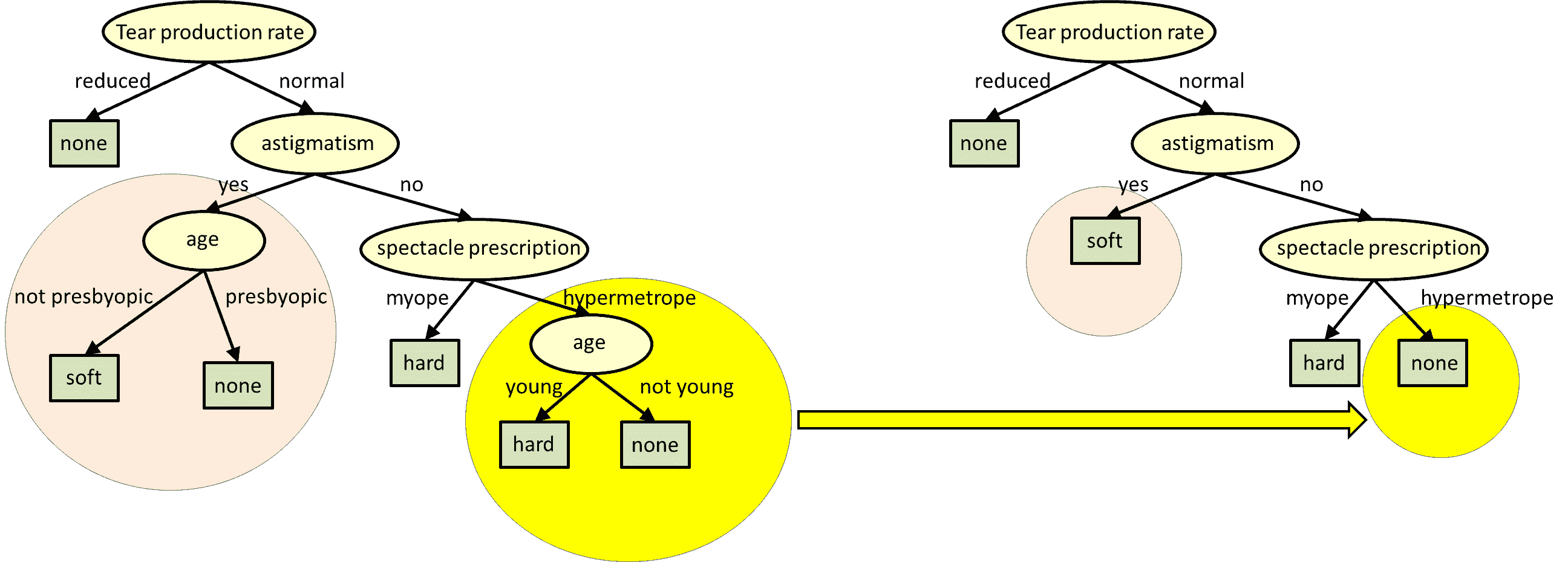
参考: http://www.cs.cmu.edu/~bhiksha/courses/10-601/decisiontrees/
如您所见,子树被更突出的结果所取代,成为新的叶子。 可以重复此过程,直到达到所需的复杂性级别,树高或信息获取量。 由于树是为了节省修剪时间而构建的,因此可以跟踪和存储信息增益。 每个模型都应使用自己的修剪算法来满足其需求。
总结
决策树使您可以快速有效地对数据进行分类。 因为它们将数据塑造为决策的层次结构,所以即使非专家也可以很好地理解它们。 决策树是通过两步过程创建和完善的:归纳和修剪。 归纳法涉及挑选最佳属性进行拆分,而修剪则有助于过滤掉认为无用的结果。 由于决策树非常易于创建和理解,因此通常是用于建模和预测数据集结果的第一种方法。
代码示例
提供的代码 Decisiontrees.py 以本文档中讨论的示例为基础,并从中创建决策树。 首先,定义每个类的每个可能选项。 稍后将其用于适应和显示我们的决策树:
# The possible values for each classclasses = {'supplies': ['low', 'med', 'high'],'weather': ['raining', 'cloudy', 'sunny'],'worked?': ['yes', 'no']}
接下来,我们创建了上面显示的数据集的矩阵,并定义了每行的结果:
# Our example data from the documentationdata = [['low', 'sunny', 'yes'],['high', 'sunny', 'yes'],['med', 'cloudy', 'yes'],['low', 'raining', 'yes'],['low', 'cloudy', 'no' ],['high', 'sunny', 'no' ],['high', 'raining', 'no' ],['med', 'cloudy', 'yes'],['low', 'raining', 'yes'],['low', 'raining', 'no' ],['med', 'sunny', 'no' ],['high', 'sunny', 'yes']]# Our target variable, whether someone went shoppingtarget = ['yes', 'no', 'no', 'no', 'yes', 'no', 'no', 'no', 'no', 'yes', 'yes', 'no']
不幸的是,sklearn 机器学习包无法根据分类数据创建决策树。 有正在进行的工作允许这样做,但是现在我们需要另一种方法来用库在决策树中表示数据。 幼稚的方法是仅枚举每个类别-例如,将晴天/阴天/阴天转换为 0、1 和 2 之类的值。但是这样做有一些不幸的副作用,例如这些值是可比较的(晴天 <正在下雨)且连续。 为了解决这个问题,我们对数据进行“一次热编码”:
categories = [classes['supplies'], classes['weather'], classes['worked?']]encoder = OneHotEncoder(categories=categories)x_data = encoder.fit_transform(data)
一种热编码使我们能够将分类数据转换为期望连续数据的 ML 算法可识别的值。 它通过选择一个类并将其划分为每个选项来工作,其中一点代表该选项是否存在。
现在我们有了适合 sklearn 决策树模型的数据,我们只需将分类器拟合到数据即可:
# Form and fit our decision tree to the now-encoded dataclassifier = DecisionTreeClassifier()tree = classifier.fit(x_data, target)
其余代码涉及创建一些随机预测输入,以显示如何使用树。 我们以与上述数据相同的格式创建了一组随机数据,然后将其传递到 DecisionTreeClassifier 的预测方法中。 这为我们提供了一系列预测目标变量-在这种情况下,对 Mike 是否会购物的答案是或否:
# Use our tree to predict the outcome of the random valuesprediction_results = tree.predict(encoder.transform(prediction_data))
参考文献
- https://towardsdatascience.com/decision-trees-in-machine-learning-641b9c4e8052
- https://heartbeat.fritz.ai/introduction-to-decision-tree-learning-cd604f85e23
- https://machinelearningmastery.com/implement-decision-tree-algorithm-scratch-python/
- https://sebastianraschka.com/faq/docs/decision-tree-binary.html
- https://www.cs.cmu.edu/~bhiksha/courses/10-601/decisiontrees/

