这个模型非常的浓厚的优化思想。

思想

SVM一开始的思想是做一个线性分类器，他的决策边界是超平面wx+b=0，他的想法就是最大化他的间隔距离。
边界的定义为wx+b=±1（这里其实用的是几何间隔，即w范数为1，因为w和b同时扩大或者缩小倍数对分类平面的选取并无影响），间隔距离依照平面到平面的距离公式可以很简单的知道为 支持向量机（SVM） - 图1。
所以得到SVM的优化模型。

Hard Margin

优化模型为
支持向量机（SVM） - 图2
数学中一般求解为min ，所以将目标变为 支持向量机（SVM） - 图3
这里加平方的原因是要变成凸二次规划问题，数学中凸二次规划有很多求解器可以选取。
支持向量机（SVM） - 图4
这就是我们常说的QP问题，可以使用拉格朗日法求解，数学中对这个问题已经研究的非常透彻了，都是有现成的算法可以求解。

Soft Margin

如果数据集线性可分，那么上面那个模型存在唯一的决策边界（唯一最优解）。
但是总会有一些outliner 他会导致你的数据集不是线性可分的，这时候我们就想加入一些处理，来解决这个问题，这就是soft 模型。
我们对每个数据 加入一个参数 支持向量机（SVM） - 图5 ，表示这个点犯了多大的错误，体现在约束条件上，支持向量机（SVM） - 图6 ，在目标函数上体现的就是一个惩罚的概念，我们引入参数支持向量机（SVM） - 图7 表示惩罚的力度。
所以我们的优化模型就变成了这个：
支持向量机（SVM） - 图8
我尝试过（鸢尾花数据集）使用 scipy 库中的近似二阶Hessen矩阵的（LBFGS，BFGS）算法，大多数都迭代未收敛，剩下的一阶算法中，CG也迭代失败了，结果最好的是SLSQP，基本上正确的返回了结果。

图中是关于对偶模型的求解：MarginC就是软间隔对偶模型的那个C。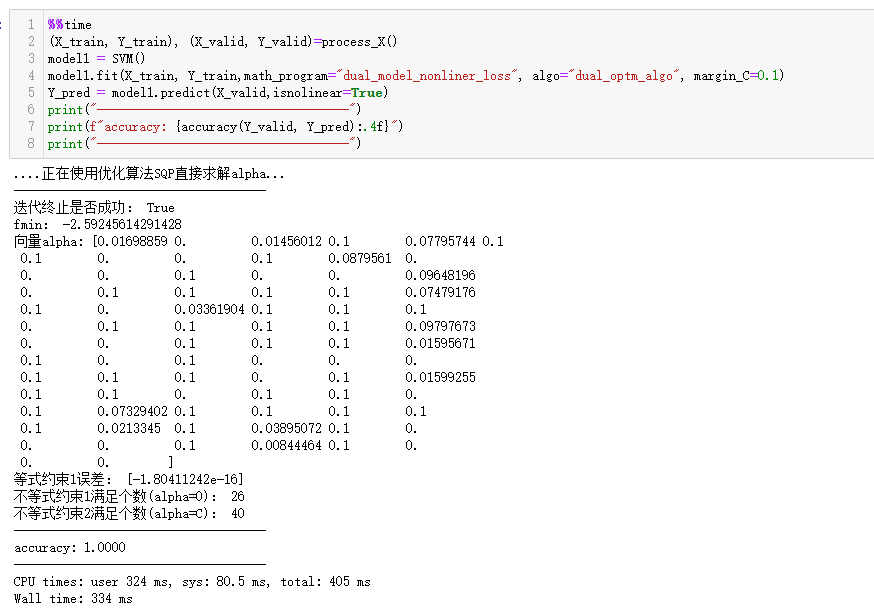
image.png

Hinge Loss

观察目标函数和约束条件，将约束条件移项，