一、简述分组卷积以其应用场景
介绍
在常规卷积中,最终输出特征图的每个通道都与输入特征图的所有通道相连接,即在“通道”这个维度上其实是全连接的。
分组卷积:将输入通道和输出通道都划分为相同的组数,然后仅让处于相同组号的输入通道和输出通道进行“全连接”
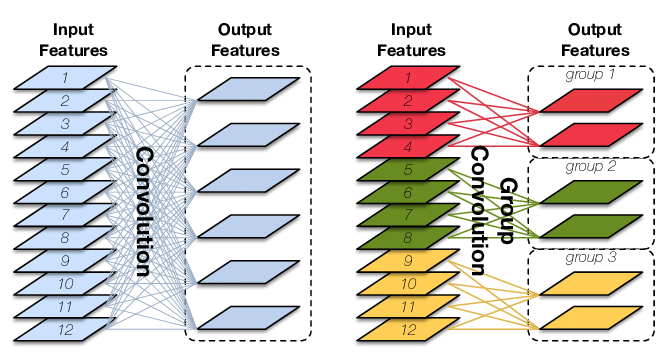
图片引用自:链接
参数量
常规卷积:
分组卷积:假设分为G组
参数量和计算量都减少为普通卷积的
应用
分组卷积最早在AlexNet网络中引入,为了解决单个GPU无法处理含有较大计算量和存储需求的卷积层这个问题。
目前多被用来构建用于移动设备的小型网络模型。
分组卷积对内存的访问频繁程度并未降低,且现有的GPU加速库对其优化的程度有限,在效率的提升上不如理论上显著。
其他
当分组数量等于输入map数量,输出map数量也等于输入map数量,Group Convolution就成了Depthwise Convolution,参见MobileNet和Xception等
如果分组数G=N=C,同时卷积核的尺寸与输入map的尺寸相同,则输出map为长度为C的向量,此时称之为Global Depthwise Convolution(GDC)
二、简述转置卷积的主要思想
介绍
普通卷积可以形式化为一个卷积乘法操作,即为输入,维度为
,
为输出,维度为
,A是由卷积核、滑动步长决定的常对角矩阵。
转置卷积 也称为反卷积,定义如下:
此时输入维度为,可以将其复原成
- 输入特征图经过普通卷积后再经过转置卷积,只是复原了形状,并不能复原具体的取值
- 转置卷积的信息正向传播与普通卷积的误差反向传播所用的矩阵相同
转置卷积本质上是对输入数据进行适当变换的普通卷积操作
应用场景
- 语义分割/实例分割:需要输出与原始图像大小一致的像素级分割结果
- 物体检测、关键点检测
- 图像的自编码器、变分自编码器、生成对抗网络
三、简述空洞卷积的设计思路
介绍
空洞卷积(Dilated/Atrous Convolution)就是在标准的卷积核中注入空洞,以增加卷积核的感受野。
扩张率r:卷积核上相邻数据点之间有r-1个空洞,填充0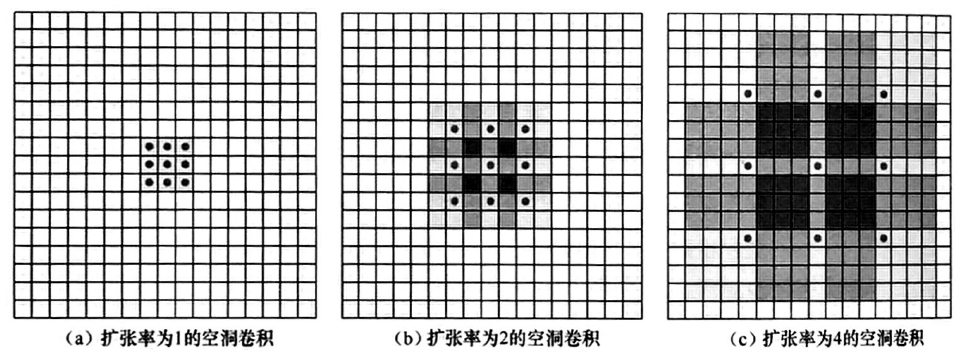
空洞卷积核的尺寸为:
四、可变形卷积旨在解决哪类问题
介绍
可变形卷积在卷积核的每个采样点上添加一个可学习的偏移量,让采样点不再局限于规则的网格点。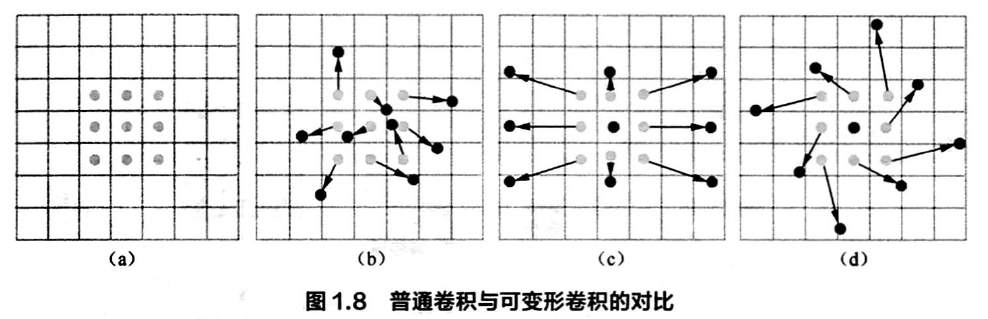
端到端的学习几何形变的偏移量,不需要额外的监督信息。 可变形卷积会根据物体的尺度,形态进行自适应调整。

