算法第五次作业－拉丁矩阵问题

张晨旭　SA20010055

问题描述

现有n种不同形状的宝石，每种宝石有足够多颗。欲将这些宝石怕排成m行n列的一个矩阵，且m<=n，使矩阵中的每一行和每一列的宝石都没有相同形状。设计一个算法，计算出对于给定的m和n，有多少种不同的排列方案。

数据输入

文件input.txt给出输入数据。第１行有２个正整数m和n，0<m<=n<9。

结果输出

将计算出的宝石排列方案输出到output.txt。

问题分析

将n种宝石编号为1到n。宝石矩阵的第一行从左到右排列为1,2,…,n，且第一列从上到下为1,2,…,m的矩阵为标准拉丁矩阵。设m行n列的标准拉丁矩阵的个数为L(m,n)。将一般的m行n列的拉丁矩阵个数记为R(m,n)。容易证明，R(m,n)=n!(n-1)!L(m,n)/(n-m)!。此问题可以转化为求解标准拉丁矩阵的个数问题。可以用教材中的排列树回溯法框架求解。

算法实现

//定义LatinMatrix类
class LatinMatrix
{
public:
    LatinMatrix();
    ~LatinMatrix();
    int solve();

private:
    void BackTrace(int id);
    void output();
    bool isOK(int row, int col);

    void ReadFile();
    void WriteFile();

private:
    int m_m;
    int m_n;
    int ** m_matrix;
    int m_solution_num;
};

//回溯法实现代码
void LatinMatrix::BackTrace(int id)
{
    if (id >= m_m * m_n)
    {
        output();
        return;
    }

    int row = id / m_n;
    int col = id % m_n;

    for (int k = 0; k != m_n; k++)
    {
        m_matrix[row][col] = k;

        if (isOK(row, col))
        {
            id++;
            BackTrace(id);
            id--;
        }
    }
}

运行结果

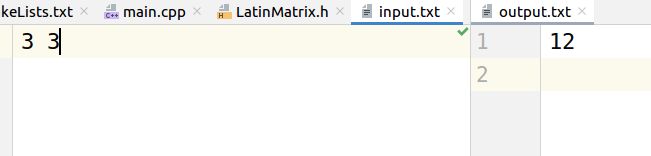
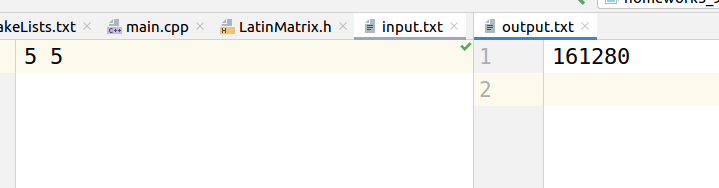
代码运行结果如下：
分别计算了33和55的拉丁矩阵个数。