原文来自
基于原笔记进行部分改动
对应于书本的2.4
对应于书本的2.4。
小结:
- 根据IEEE标准,可以将浮点数划分为 非标准化,标准化,特殊值。对于非标准化和标准化的 M,E 公式不同。
- 在浮点数舍入时,常使用偶数舍入,能够得到更平均的值
- 浮点数运算需要考虑 舍入 和 溢出的问题,对于 M 还需要考虑左移和右移的情况
1. 浮点数简介
浮点表示对形如 的有理数进行编码,比较适用于非常大的数字、非常接近0的数字。它常常不会太多关注运算的准确性,而是把实现的速度和简便性看得比数字精确性更重要。1985年提出了IEEE标准754,仔细制定了表示浮点数机器运算的标准,后续所有计算机都支持这个标准,极大提高了程序可移植性。
首先会介绍IEEE浮点表示方法,然后由于数字不能精确被表示,所以会介绍浮点数的舍入问题。最后介绍浮点数相关的运算。
2. IEEE浮点表示
IEEE浮点表示使用 表示数字。其中包含三部分:
- 符号(Sign)s:用来确定V的正负性,当s=0时表示正数,s=1时表示负数。用一个单独的符号位直接进行编码。
- 尾数(Significand)M: 是一个二进制小数,通常介于1和2之间的小数。使用n位二进制进行编码的小数。
- 阶码(Exponent)E:对浮点数进行加权。使用k位进行编码的正数
。使用无符号整数的解码方式
C语言中有单精度精浮点数float,其中s=1、k=8、n=23;还有双精度浮点数double,其中s=1、k=11、n=52。
我们可以根据尾数和阶码的不同取值,将其分成三种情况:
- 规格化的值(normalized):
,其中
,由此能将E重新投影到正负值,并且能够和非规格化进行平滑转变。
,因为我们可以通过调整E使得
,所以通过这种形式将尾数变成
的形式,就能获得额外的精度。规格化数能够表示大范围的数。
- 非规格化的值(denorm):
,由此来保证和规格化值的连续性
。非规格化数能够表示正负0以及趋近于0的数。
- 特殊值(special):
- exp 全为1,frac 全为0,表示无穷,s = 0是正无穷,s = 1是负无穷
- exp 全为1,frac 不全为0,表示不存在的数:NAN
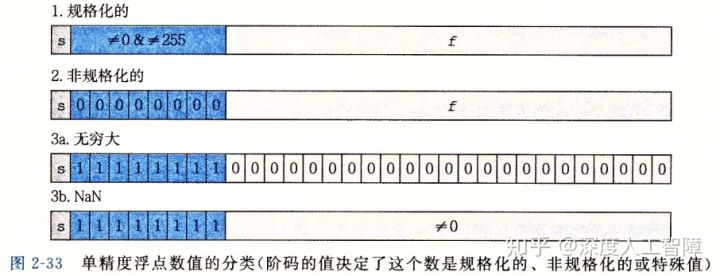

通过上面我们可以观察到几个现象:
- 非规格数稠密地分布在靠近0的区域
- 有些数的间隔是等距的,因为当 exp 值不变,在 frac 尾数区域进行增加会乘上相同的指数
- 越大的数间隔越大,因为比较大的数,它的指数 2^E 会比较大,使得每次变化量会比较大。
我们以正数为例(s=0),说明几个比较特殊的值:
- 0:只有非规格化才能表示0,exp 和 frac 全部为0时,结果为0。
- 最小的正非规格化数:
是固定值,在
取值范围内的最小值正数是
,则
,所以
- 最大的非规格化数:
是固定值 ,在 frac 取值范围内的最大值是
,则
,所以
。
- 最小规格化数:exp 最小为
,此时
。 frac 全为0时,M 取得最小值 1,所以
- 1:要让V = 1,很容易想到让
,即
,此时 frac = [0,0,0…0], exp = [0,1,1…1]
- 最大规格化数:exp 最大为 [1,1,1…0],此时 E = exp - Bias = 2^k - 2 - (2^{k-1} - 1) = 2^{k-1} - 1,M 取得最小值 2 - 2^{-n},所以 V = (2 - 2^{-n})\times 2^{2^{k-1} - 1}
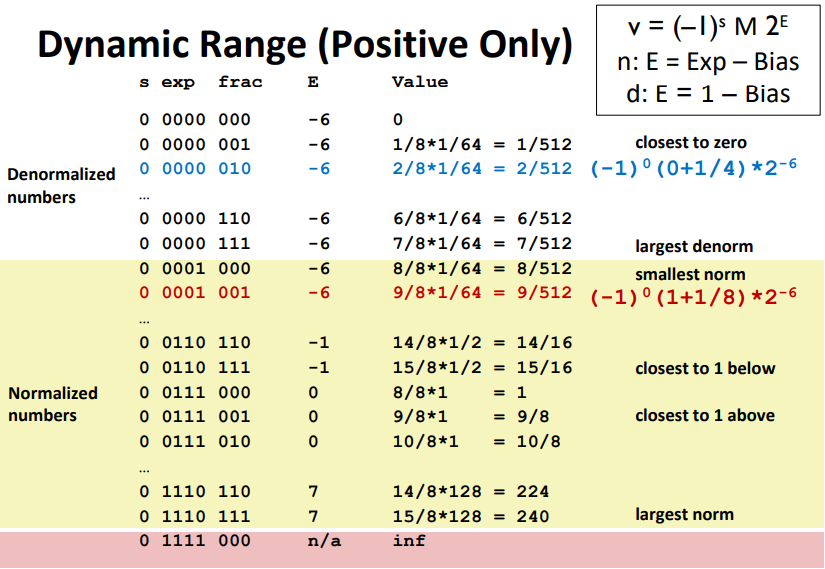
IEEE设计的好处:
- 最大非规格化值 (1 - 2^{-n})\times 2^{2 - 2^{k-1}} 和最小规格化值 2^{2 - 2^{k-1}} 之间的幅度是 ,2^{-n} 是n位尾数所能表示的最小值,可以看成是光滑转变。
- 从最小非规格化数到最大规格化数的位向量的变化是顺序的,和无符号整数的排序相同。所以除了NAN外,可以用无符号数的排序函数来对浮点数进行排序。 注意:负无穷转化为无符号数进行比较时会有问题。
- exp 设置为无符号数,再通过 Bias 转变为有符号数的方式,可以使得浮点数的比较结果 = 无符号整数的比较结果。如果让 exp 设置为有符号数,不会有这种效果
- M 设置为1 + frac 的形式,可以节省一位的空间,表示更大的范围。
2.1 十进制转为浮点数表示
步骤:
- 计算 Bias = 2^{k-1}-1
- 计算阶码的值 exp 和尾数的值 frac
- 根据 exp 判断编码属于哪一类值,并使用不同的编码方式:规格化:E = exp - Bias,M = 1 + frac。非规格化:E = 1 - Bias,M = frac。特殊值:exp 全为1,根据 frac 判断是NAN还是无穷值。
- 计算最终的值 V = (-1)^s \times M \times 2^E
样例:
以12345为例,我们可以推算单精度浮点数的编码:s=1、k=8、n=23
- 计算 Bias = 2^{k-1} - 1 = 2^7 - 1 = 127
- 将12345化为二进制数 [11000000111001]
- 首先将二进制数转为小于1的科学计数法 0.11000000111001 \times 2^{14},由于指数14不是 1-Bias = -126,所以是规格化数,可以将其转化为大于一的科学计数法 1.1000000111001 \times 2^{13},所以 M = 1.1000000111001, E = 13
- 因为 M = 1 + frac,所以 frac 的编码为 [1000000111001]。因为 E = exp - Bias = exp - 127,所以 exp = 127 + 13 = 140 = [10001100]。
- 将frac 和 exp 的二进制编码扩展到对应位数后拼接,补上符号位 = 最终结果 01000110010000001110010000000000
注意:记得要在exp前面补0,在frac后面补0。因为exp表示整数,frac表示小数
2.2 浮点数转为十进制表示
步骤:
- 根据 exp 判断二进制编码属于哪一类值: 规格化,非规格化,特殊值
- 计算 Bias
- 根据二进制编码的类型,得出 E 和 M 的值
- 计算最终的值 V = (-1)^s \times M \times 2^E
样例:
将单精度编码 01000110010000001110010000000000 转变为十进制表示
- 由于k = 8,n = 23,exp = [10001100],因此这个数是一个规格化数
- 由于k = 8,因此可以计算出 Bias = 2^7 - 1 = 127
- 计算出 exp = 140,E = exp - Bias = 13。由于 M = 1 + frac,frac = [1000000111001],可以计算出 M = 1.1000000111001
- V = M \times 2^E = 1.1000000111001 \times 2^{13} = 12345
3. 浮点数舍入
浮点数由于有限的位数,所以对于真实值x,我们想要用一种系统的方法来找到能够用浮点数表示的“最接近的x”匹配值x’,这个过程就称为舍入。
常见的舍入方法有四种:向零舍入、向上舍入、向下舍入以及向偶数舍入。以十进制为例可以看以下表格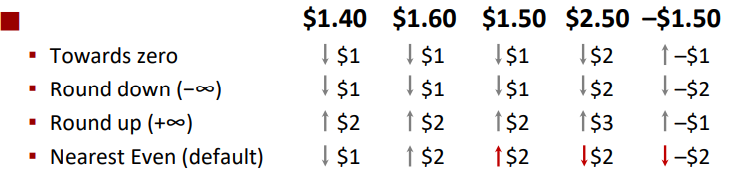
其中比较特殊的是向偶数舍入:如果处于中间值,就朝着令最后一个有效位为偶数来舍入;否则朝着最近的值舍入。比如1.40,由于靠近1就朝1舍入;1.6靠近2就朝2舍入;1.50位于十进制的中间值,就朝着偶数舍入,所以为2。
向偶数舍入的意义:如果对一系列值进行向上舍入,则舍入后的平均值会比真实值更大;使用向下舍入,则舍入后的平均值会比真实值更小。通过向偶数舍入,每个值就有50%概率变大、50%概率变小,使得总的统计量保持较为稳定。
十进制的中间值为 500…{10},比这个中间值大就向上舍入,比这个中间值小就向下舍入,否则朝着偶数舍入。
而二进制的中间值为 100…{2},比如 101…{2} 就比中间值大, 001…{2}就比中间值小。而且二进制中,当最后一个有效位为0时,为偶数。比如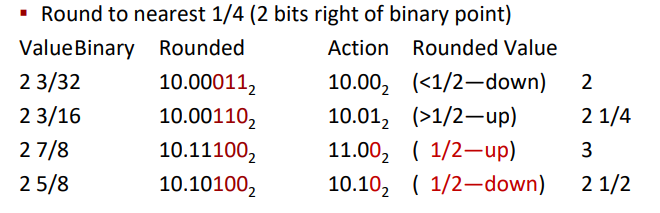
如图小数点后取两位有效位。中间值为.00100
- 10.00011:由于011比中间值小,所以直接向下舍入,为10.00。
- 10.00110:由于110比中间值大,所以直接向上舍入,为10.01。
- 10.11100:由于100为中间值,而10.11最后一个有效位1为奇数,所以向上舍入为偶数11.00。
10.10100:由于100为中间值,而10.10最后一个有效位0为偶数,所以直接向下舍入10.10。
4. 浮点数运算
4.1 浮点数乘法
对于两个浮点数 (-1)^{s1} \times M{1} \times 2^{E_{1}} 和 (-1)^{s2} \times M_2 \times 2^{E_2},计算结果为 (-1)^s \times M \times 2^E,其中 s = s1~XOR~s2,M = M_1 \times M_2,E = E_1 + E_2。
如果M >= 2,需要将frac右移一位,并对E加一。
- 如果 E 超过了表示范围,就发生了溢出。上溢出会得到INF值,下溢出会得到 0。
- 如果M超过了表示范围,对frac进行舍入。
- 首先进行0检查,如果一个为0,就不会进行浮点数乘法
数学性质:
- 可交换
- 不可结合:结合可能会出现溢出和不精确的舍入,比如 10^{20} (10^{20} 10^{-20}) = 10^{20},而 (10^{20}10^{20})10^{-20} = INF。
- 不可分配:如果分配了可能会出现 NAN,比如10^{20}(10^{20}-10^{20}) = 0,而 10^{20} 10^{20} - 10^{20}*10^{20} = NAN。
- 保证:只要 a ≠ NAN,那么 a*^{t}a >= 0
单调性:a >= b && c >= 0 ,可以推出 a c >= b c
4.2 浮点数加法
对于两个(-1)^{s1} \times M{1} \times 2^{E_{1}} 和 (-1)^{s2} \times M_2 \times 2^{E_2},计算结果为 (-1)^s \times M \times 2^E,其中s和M是运算结果,E = max(E1,E2)
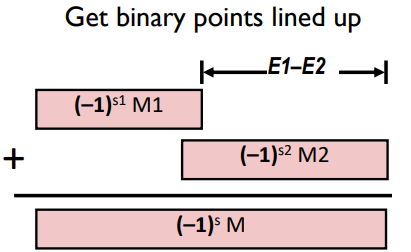
如果 M >= 2,则 frac 右移一位,并对 E 加一
- 如果 M < 1,则 frac 左移一位,并对 E 减一
- 如果 E 超过表示范围,就发生溢出
- 如果 M 超过表示范围,就对frac进行舍入
数学性质:
- 由于溢出,可能得到无穷之。
- 可交换
- 不可结合(由于舍入),因为较大的数和较小的数相加,由于舍入问题,会将较小的数舍入,比如
而
。
- 除了无穷和NaN,存在加法逆元。
- 满足单调性,如果
,则对于任意a、b和x,都有
。NaN除外。无符号数和补码由于溢出会发生值的跳变,所以不满足单调性。
注意:需要考虑好清楚数值的范围,如果计算的数值范围变化很大,需要重新结合或改变运算顺序,避免由于溢出或舍入出现计算问题。
样例:
步骤:
- 对阶:将两个操作数的小数点位置对齐,使得两个数的阶码相等。
- 尾数求和:对对阶后的尾数(frac) 按定点数进行运算,需要对结果进一步规格化处理
- 规格化:M >= 2,需要让frac右移,E + 1;M < 1,需要让 frac 左移一位,E 减一。
- 舍入:由于 frac 的位数有限,因此对运算结果舍入,还原成 IEEE的方法
求 1.010 2^2 + 1.110 2^3 的计算结果,假设尾数为3位
- 对阶:两个小数结合成为 (1.010 + 11.100 ) * 2^2
- 尾数求和:frac = (1.010 + 11.100)2^2 = (100.110) 2^2
- 规格化:(100.110) 2^2 = 1.00110 2^4
- 舍入:舍入时,1.001|10 向偶数舍入,则 1.001|10 = 1.010,最终结果 = 1.010 * 2^4
5. C中的浮点数
C中提供了float和double两种精度的浮点数。由于编码不同,所以在浮点数和整型数之间强制类型转换时,会修改编码,并且会出现溢出和舍入。
- float/double转换成int:首先小数部分会被截断,也就是向0舍入。 在float不超过int范围时, float的尾数部分为23字节,比int的32字节小,int可以精确表示float的整数部分,而double的尾数有52位,可能会出现舍入;而当超过int的取值范围或NaN时,微处理器会指定 [100…0]为整数不确定值,即对应的TMIN,一个很大的浮点数转化为int时,可能会出现负数。
- int或float转换为double:double尾数有52位,而int只有32位,float只有23位,所以double会精确表示int和float,不会出现溢出和舍入。
- int转换为float:不会发生溢出,但是由于float尾数位数比较少,会出现舍入。
- double转换为float:可能会出现溢出和舍入。
总结:超过数值表示范围,会发生溢出;尾数较短,会发生舍入。
课堂作业:
- x == (int)(float) x:x从int转化为float,会发生舍入,错误。
- x == (int)(double) x:x从int转化为double,不会发生舍入,正确
- f == (float)(double) f:f从float转化为float,不会发生舍入,正确
- d == (double)(float) d:d从double转化为float,会发生舍入,错误
- f == -(-f):只是改变了两次符号位,不会发生舍入,正确
- 2/3 == 2/3.0:2/3会发生舍入,错误
- d < 0.0 推出 ((d2) < 0.0):即使d2溢出后,也是NAN,因此不影响结果,正确
- d > f 推出 -f > -d:改变符号位不会发生溢出,正确
- d d >= 0.0:保证d不是NAN时,一定成立,dd >= 0.0,溢出时结果 = 正无穷
- (d+f)-d == f:可能会舍入,错误

