什么是递归？

C 语言允许函数调用自己，这种调用过程称为递归(recursion)。
我们来看一个简单的递归示例 —— 计算阶乘的函数，并计算 0~9 的阶乘值。

#include<stdio.h>
int factorial(int);
int main()
{
    int n = 10;
    for (int i = 0; i < n; i++)
        printf("(%d!) = %d\n", i, factorial(i));
    getchar();
    return 0;
}
int factorial(int a)
{
    if (a < 2)
        return 1;
    return factorial(a - 1) * a;
}

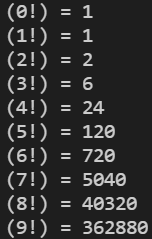
递归有时难以捉摸，有时却很方便实用。结束递归是使用递归的难点，因为如果递归代码中没有终止递归的条件测试部分，一个调用自己的函数会无限递归。
可以使用循环的地方通常都可以使用递归。有时用循环解决问题比较好，但有时用递归更好。递归方案更简洁，但效率却没有循环高。

递归的基本原理

初次接触递归会觉得比较难以理解，为了帮助大家理解递归过程，讲解几个递归的要点。

1. 每级函数调用都有自己的变量。
2. 每次函数调用都会返回一次。当函数执行完毕后，控制权将被传回上一级递归。程序必须按顺序逐级返回递归。
3. 递归函数中位于递归调用之前的语句，均按被调函数的顺序执行。
4. 递归函数中位于递归调用之后的语句，均按被调函数相反的顺序执行。
5. 虽然每级递归都有自己的变量，但是并没有拷贝函数的代码。程序按顺序执行函数中的代码，而递归调用就相当于又从头开始执行函数的代码。除了为每次递归调用创建变量外，递归调用非常类似于一个循环语句。实际上，递归有时可用循环来代替，循环有时也能用递归来代替。
6. 递归函数必须包含能让递归调用停止的语句。通常，递归函数都使用if或其他等价的测试条件在函数形参等于某特定值时终止递归。为此，每次递归调用的形参都要使用不同的值。

为了方便演示上面的几个要点，在阶乘函数中加入了一些输出信息。

#include<stdio.h>
int factorial(int);
int main()
{
    printf("main: (4!) = %d\n", factorial(4));
    return 0;
}
int factorial(int a)
{
    printf("start: a = %d, &a = %p\n", a, &a);
    if (a < 2) {
        printf("end: a = %d, &a = %p\n", a, &a);
        return 1;
    }
    int result = factorial(a - 1) * a;
    printf("end: a = %d, &a = %p\n", a, &a);
    return result;
}

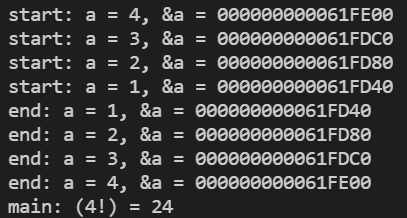
可以看到计算 4 的阶乘的时候有四级调用，第一级调用是 factorial(4)，第二级调用是 factorial(3) …。每一级调用中的形式参数 a 都是不同的，这一点可以通过它们的地址来看出来。递归调用之前的输出信息语句是按照递归调用的顺序输出的(4 3 2 1)，而递归调用之后的输出信息语句是逆序的(1 2 3 4)。

尾递归

最简单的递归形式是把递归调用置于函数的末尾，即正好在 return 语句之前。这种形式的递归被称为尾递归(tail recursion)，因为递归调用在函数的末尾。尾递归是最简单的递归形式，因为它相当于循环。我们前面的计算阶乘的函数就是尾递归。

既然用递归和循环来计算阶乘都没问题，那么到底应该使用哪一个？
一般而言，选择循环比较好。首先，每次递归都会创建一组变量，所以递归使用的内存更多，而且每次递归调用都会把创建的一组新变量放在栈中。递归调用的数量受限于内存空间。其次，由于每次函数调用要花费一定的时间，所以递归的执行速度较慢。

既然递归执行速度较慢，为什么还要学习递归？
尾递归是递归中最简单的形式，比较容易理解。在某些情况下，不能用简单的循环代替递归，因此读者还是要好好理解递归。

倒序计算

递归在处理倒序时非常方便（在解决这类问题中，递归比循环简单）。
例如，编写一个函数，输入一个整数，打印这个整数的二进制数。

#include<stdio.h>
void binary(int);
int main()
{
    int a;
    scanf("%d", &a);
    binary(a);
    return 0;
}
void binary(int a)
{
    if(a/2)
        binary(a/2);
    printf("%d", a%2);
}

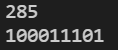
不用递归，是否能实现这种用二进制形式表示整数的算法？
当然可以。 但是由于这种算法要首先计算最后一位二进制数，所以在显示结果之前必须把所有的位数都储存在别处（例如，数组）。

递归的优缺点

递归既有优点也有缺点。
优点：递归为某些编程问题提供了最简单的解决方案。
缺点：一些递归算法会快速消耗计算机的内存资源。另外，递归不方便阅读和维护。

我们再来举一个典型的例子，斐波那契数列。
斐波那契数列的定义如下：第1 个数字和第 2 个数字都是 1，而后续的每个数字都是其前两个数字之和。例如，该数列的前几个数是：1、1、2、3、5、8、13。

用数学上的数列来描述的话就是：

首先，我们来看看递归的实现。递归提供一个简单的定义。如果把函数命名为 Fibonacci()，那么如果 n 是 1 或 2， Fibonacci(n) 应返回 1，对于其他数值，则应返回 Fibonacci(n-1) + Fibonacci(n-2)。代码如下：

unsigned long Fibonacci(unsigned n) 
{
    if (n < 3) 
           return 1; 
    return Fibonacci(n-1) + Fibonacci(n-2);
}

这个递归函数只是重述了数学定义的递归。该函数使用了双递归(double recursion)，即函数每一级递归都要调用本身两次，这就造成了一个问题。
为了说明这个问题，假设调用 Fibonacci(40)。这是第 1 级递归调用，将创建一个变量 n。然后在该函数中要调用 Fibonacci() 两次，在第 2 级递归中要分别创建两个变量 n。这两次调用中的每次调用又会进行两次调用，因而在第 3 级递归中要创建 4 个名为 n 的变量。此时总共创建了 7 个变量。由于每级递归创建的变量都是上一级递归的两倍，所以变量的数量呈指数增长！按指数增长很快就会产生非常大的值。在本例中，指数增长的变量数量很快就消耗掉计算机的大量内存，很可能导致程序崩溃。
虽然这是个极端的例子，但是该例说明：在程序中使用递归要特别注意，尤其是效率优先的程序。

所有的 C 函数皆平等。程序中的每个 C 函数与其他函数都是平等的。每个函数都可以调用其他函数，或被其他函数调用。这点与 Pascal 和 Modula-2 中的过程不同，虽然过程可以嵌套在另一个过程中，但是嵌套在不同过程中的过程之间不能相互调用。
main() 函数是否与其他函数不同？是的，main() 的确有点特殊。当 main() 与程序中的其他函数放在一起时，最开始执行的是 main() 函数中的第 1 条语句，但是这也是局限之处。main() 也可以被自己或其他函数递归调用 —— 尽管很少这样做。