算法 - 二叉树 - 简单

1、二叉树的最大深度

给定一个二叉树，找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例：
给定二叉树 [3,9,20,null,null,15,7]

    3
   / \
  9  20
    /  \
   15   7

返回它的最大深度 3

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var maxDepth = function(root) {
    if(!root) return root
    let result = 1;
    function dfs(node, deepNum){
        if(node.left === null && node.right === null){
            result = Math.max(result, deepNum);
            return;
        }
        node.left !== null && dfs(node.left, deepNum + 1)
        node.right !== null && dfs(node.right, deepNum + 1)
    }
    dfs(root, 1);
    return result
};

2、二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

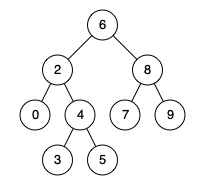
示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
var lowestCommonAncestor = function(root, p, q) {
    if(root.val > p.val && root.val > q.val){
        return lowestCommonAncestor(root.left, p, q)
    }
    if(root.val < p.val && root.val < q.val){
        return lowestCommonAncestor(root.right, p, q)
    }
    return root
};

3、路径总和

给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。

说明: 叶子节点是指没有子节点的节点。

示例:
给定如下二叉树，以及目标和 sum = 22，

          5<br />             /  \<br />            4   8<br />           /   /   \<br />        11 13   4<br />        /  \          \<br />      7    2          1

返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} sum
 * @return {boolean}
 */
var hasPathSum = function(root, sum) {
    function dfs(node, val){
      if(node.left === null && node.right === null
  }
};