数据结构---并查集

参考（部分内容和图片来源于以下参考，如有侵权，联系删除）：
https://zhuanlan.zhihu.com/p/93647900/

什么是并查集？

就是一个集合。

有什么实际应用？

除了算法题中见到，好像其他地方还没用过。

并查集的基本结构

图例：

1. 初始状态，共6个节点，也就是6个集合，每个集合中只有一个元素，并且每个元素的父节点是它本身：

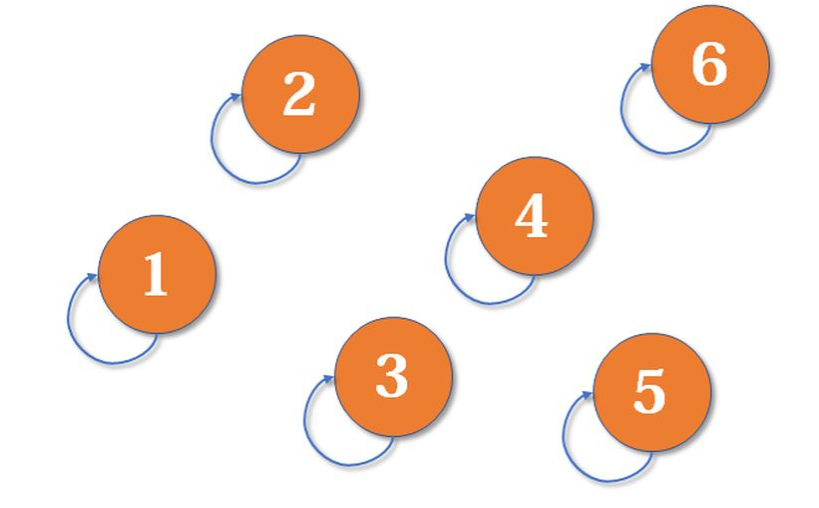
1. 现在，需要将两个集合合并（取并集），3合并到1中，原本独立的两个集合{1}{3}变成了{1,3}，并且3的父节点变成了1，现在1,3是在同一个集合中的了。

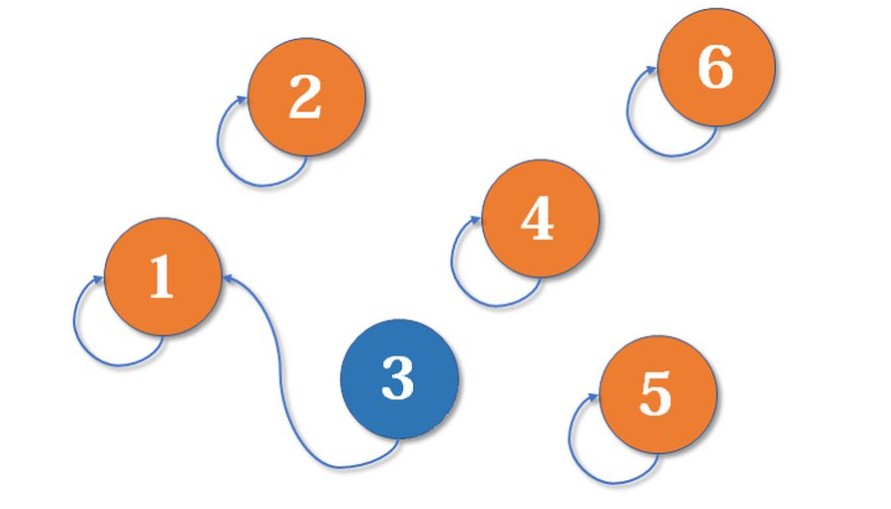
1. 同样的道理，2又合并到1所在的集合中，现在2的父节点变成了1,1原本在的集合变成了{1, 2, 3}，2所在的单独集合已经没了（合并到了1中）。

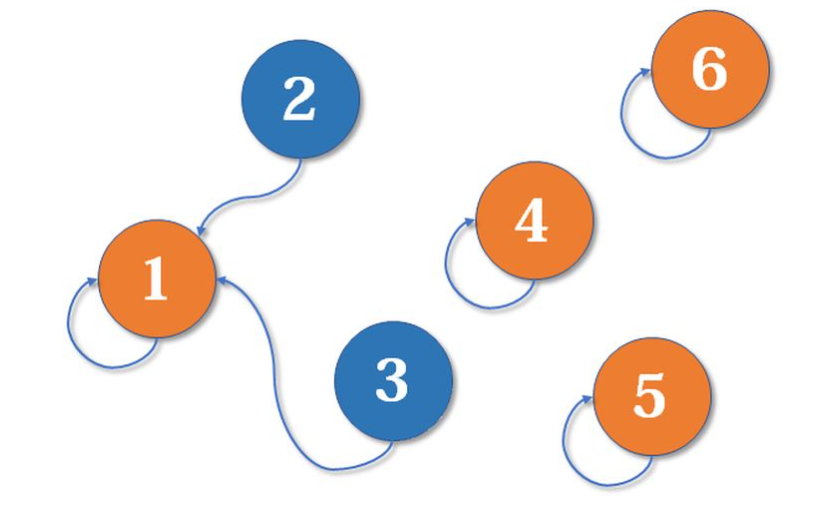
1. 同样的，任何两个节点直接都是可以合并的（任何两个集合都是能取并集的），{4}，{5}，{6}三个集合合并，就变成了了下面这个：

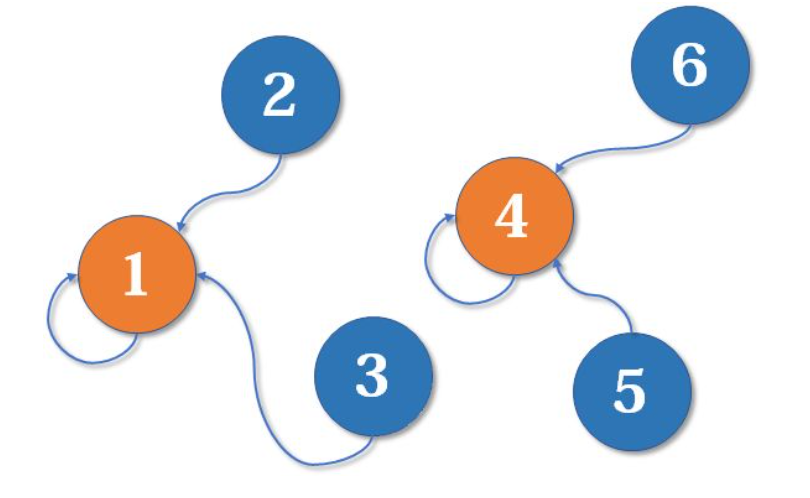
1. 现在，就剩下两个集合了，我们要将这两个集合进行合并的话是怎么样的呢，可以选择把4的父节点指到1，也可以选择把1的父节点指到4（两个集合的根，谁作为子节点对于并查集的性能优化有用）。

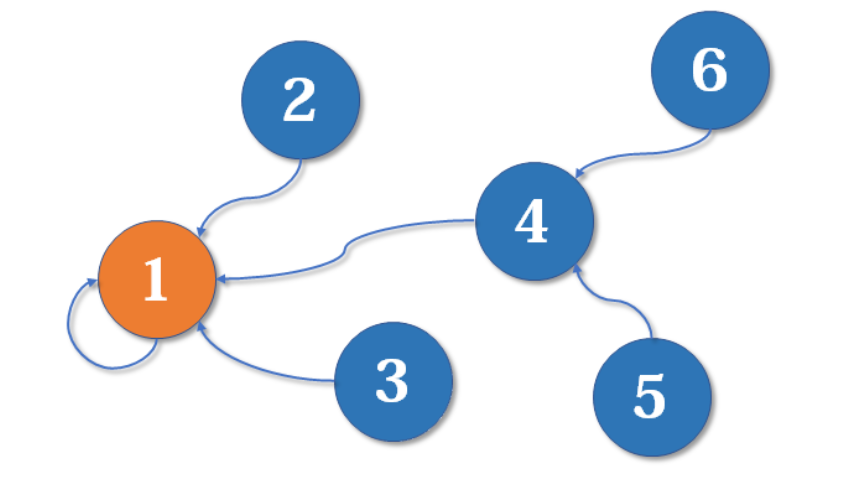
之后，对并查集的使用也就两种：
1）两个集合进行合并
2）查找某个元素的根节点（这用于判断两个元素是否在同一个集合中）。

并查集的实现

以一道简单的例题来看（例题有测试用例，较大程度保证自己写错了能够发现）：
https://leetcode-cn.com/problems/redundant-connection/

题意：
给你一个图，这个图是由一颗树加上一条边之后得到的，现在给你所有的边，让你找出去掉哪条边之后得到的还是一棵树（而不是没分成了两棵树）。

转变一下思路，去掉一条边还是树，实际上就是原本加上这条边之后就出现了环呗。那好办了，直接通过不断加入 边，通过并查集判断边上的两个顶点是不是同一个集合中，在同一个集合中就是环了，不在就不是环，加入到集合中，形成树。

1. 数组实现（算法题中一般用的最多的就是数组实现，毕竟数据范围给定，一次开满空间，通过数组的映射进行查找是快速又简便的）

代码实现：这个长度数组是按秩合并进行优化用到的，在query方法中还有一个路径压缩。整体代码也比较固定，10几行。下面详细说说这个路径压缩和按秩合并。

class Solution {
public:
    int fa[1005];
    int length[1005];
    int max_node;
    void init(){
        for(int i = 1; i <= max_node; i++){
            fa[i] = i;
        }
    }
    int query(int x){
        if(fa[x] == x)return x;
        return fa[x] = query(fa[x]);
    }
    void merge(int p, int q){
        int a = query(p), b = query(q);
        if(a == b)return;
        if(length[a] > length[b]){
            fa[b] = a, length[a]++;
        }else{
            fa[a] = b, length[b]++;
        }
    }
    vector<int> findRedundantConnection(vector<vector<int>>& edges) {
        vector<int> ans(2);
        for(int i = 0; i < edges.size(); i++){
            max_node = max(max_node, max(edges[i][0], edges[i][1]));
        }
        init();
        for(int i = 0; i < edges.size(); i++){
            int a = edges[i][0], b = edges[i][1];
            if(query(a) == query(b)){
                ans[0] = a, ans[1] = b;
            }else{
                merge(a, b);
            }
        }
        return ans;
    }
};

路径压缩：
就是节点指向的父节点，始终保持指向集合的根节点，保持树的高度最低。下面几个图进行理解（图片待补充）。

按秩合并：
就是在合并两个集合的时候，把高度低的树作为高度高的树的子节点，以保持整个树的高度更低。如下图（图片待补充）：

面向对象封装

c++:

java：

应用例题：

acwing:

leetcode: