2.6 浮点数

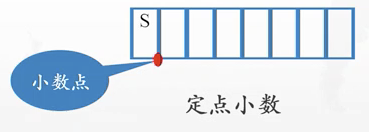
小数应该怎么表示？

核心难点：

• 小数点怎样处理？

• 不同的数，小数点位置不同。小数点的位置在哪里，怎么表示？

  定点数：

  实现约定好小数点的位置。小数点在数中的位置是固定的。

  定点整数（纯整数）：

  小数点定在数的最后，也就是D0位。
  

  定点小数（纯小数）：

  小数点定在数的最前面、或紧跟符号位之后。
  

  浮点数

  基本思想：

  采用科学计数法的形式来表示数值

  生活中的科学计数法：

  光速：3 * 10 (米/秒)

  表现形式

  生活中采用十进制，因此生活中的科学计数法是把一个数表示成「十进制数10」的形式
  计算机中采用二进制，因此计算机中的科学计数法是把一个数表示成「二进制数2」的形式
  
  任何一个二进制数，一定可以写成如下形式：正负1点几乘以2的正负n次方
  
  二进制的每一位，肯定是0或1。只要这个数不是整数0，则二进制的表现上，肯定有一个1的存在。
  因此，总是可以把小数点儿运动到最前面的1之后，写成下图的这种标准格式：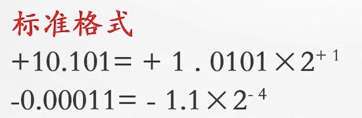
  

  浮点数的构造过程

  当我们将一个二进制数以上述的形式处理成标准格式后，我们只需要采集四个关键信息，就能在必要的时候，通过代入公式计算出这个数的值。这就是浮点数的构造过程。
  

  数符：

  最前边的正负号

  尾数：

  m，是一个定点小数

  阶符：

  指数的正负号

  阶码：

  n，是一个定点整数

  注意：

  具体的存储格式、尾数和阶码各占多少位？对不同的数据类型有不同的规定。

  浮点数分类

  大多数系统中，分为两类：单精度浮点数、双精度浮点数

  单精度浮点数

  长度为4个字节（个别系统）

  双精度浮点数

  长度为8个字节（个别系统）

  区别是：

• 数位长度不一样（单4双8）

• 双精度浮点数精确度更高，取值范围更广：可以用来表示特别大或特别小的数。

  数位变多的好处：

  数符和阶符都是正负号，用0或1表示（0表示正，1表示负）。位数变长对二者没有影响，也就是说，位数变长实际上影响的是尾数和阶码：
  尾数的位数决定数的精度、阶码的位数决定数的范围

• 尾数越长，表示数的精确度越高；

• 阶码越长，表示数的取值范围越大；
• 阶符为正时，阶码越大，数绝对值越大；
• 阶符为负时，阶码越大，数绝对值越小。

  浮点数的不精确性：

  导致浮点数不够精确的情况一：

  在数轴上的任意区间内，实数有无限个；但是在同一区间内浮点数的个数是有限的。
  例如：四个字节表示浮点数，则其个数有2个，约40亿个。
  为了实现「有限个」数表示「无限个」值，浮点数表示数据时常采用近似值。

  这也就解释了，为什么控制台中计算0.1 + 0.2 得到的数据不是正确的0.3，而是好多位的浮点数，就是因为计算机内部浮点数表示时，采取的是近似值。

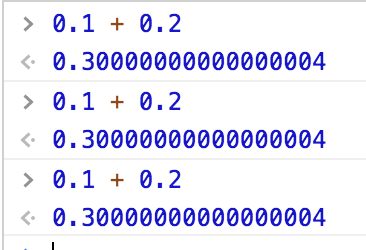
另外一个情况加剧了浮点数的不精确性：

浮点数在数轴上的分布是不均匀的。
当阶符为负时，浮点数的绝对值小于1；
当阶符为正时，浮点数的绝对值大于1；
所以把数轴分成四段：

• 负无穷～-1
• -1～0
• 0～1
• 1～正无穷

这四段中，每一段内浮点数的个数都大致相同，每一段内大约10亿个浮点数。
上图可以看出以下规律：

• 在-1～0、0～1这两段之间（也就是接近-1～1的区间段附近），数轴上更短的距离可以表示更多的数，所以数据密度是很大的，近似值更接近、表示的数也就更加精确；
• 而-1向左端、+1向右端这两段，越向数轴的两端延伸，数据的密度就越稀疏，越不精确。

  浮点数标准

  

  问题

  浮点数的构造

  浮点数构造时会给价码加上偏移量，以消除阶符，使价码成为无符号数。这一设计有什么优点？