二叉树

概念：二叉树是n(n>=0)个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树组成
例如:普通的二叉树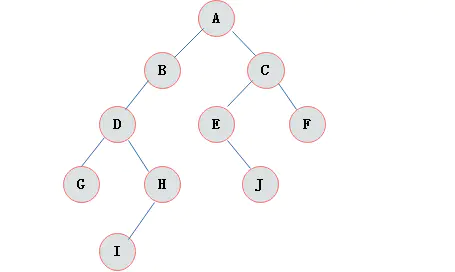

特点:

• 每个结点最多有两颗子树，所以二叉树中不存在度大于2的结点
• 左子树和右子树是有顺序的，次序不能任意颠倒
• 即使树中某结点只有一棵子树，也要区分它是左子树还是右子树

性质：

一个编号为 i 的结点有如下特性 (1) 若 i=1，则该结点是二叉树的根，无双亲, 否则，编号为 [i/2] 的结点为其双亲结点; (2) 若 2i>n，则该结点无左孩子， 否则，编号为 2i 的结点为其左孩子结点； (3) 若 2i+1>n，则该结点无右孩子结点， 否则，编号为2i+1 的结点为其右孩子结点。

比较极端的树：
左斜树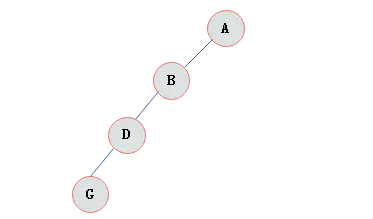

右斜树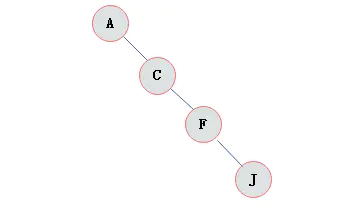

二叉树的遍历也是一个重点，在许多数据结构中，需要考虑遍历的次数，遍历一次，也就意味着耗费时间，耗费性能，在最差的情况下，一棵二叉树是左斜树或者右斜树，递归的层数为 N，它的时间复杂度就是O(n)，在最好情况下，当二叉树为平衡二叉树时，它的高度为 log⁡(N)，此时空间复杂度为 O(log⁡(N))。