本文写于2017-11-01，其中的一些思路可能存在问题，公式也未用LATEX编写。本文移至此处时暂未重新学习。

    φ(n)表示1到n-1中与n互质的数的个数，性质：

    • if(isprime(n)) φ(n)=n-1;
    • if(gcd(m,n)==1) φ(mn)=φ(m)φ(n);
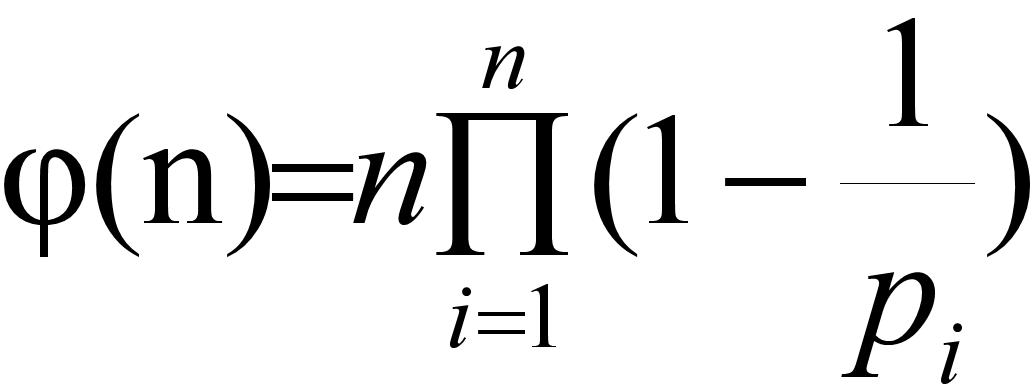
    • 欧拉函数 - 图1
    • if(n%2) φ(n)=φ(2*n);
    • if(n%p==0&&isprime(p))φ(np)=φ(n)p
      if(n%p!=0&&isprime(p))φ(np)=φ(n)p
    • 1~n比n小且与n互素的数的总和为 sum(n) = n * φ(n) / 2
    • 若已知m与n互质，则n-m也与n互质

    筛法求φ(n)：类似于素数筛，另建一个φ[n]数组，初始值φ[i]=i;每次用k筛到φ[i]时给φ[i]乘上(1-1/k)。但是这样不能使用素数线性筛。