277-leetcode

Suppose you are at a party with n people (labeled from 0 ton - 1) and among them, there may exist one celebrity. The definition of a celebrity is that all the othern - 1 people know him/her but he/she does not know any of them.

Now you want to find out who the celebrity is or verify that there is not one. The only thing you are allowed to do is to ask questions like: “Hi, A. Do you know B?” to get information of whether A knows B. You need to find out the celebrity (or verify there is not one) by asking as few questions as possible (in the asymptotic sense).

You are given a helper function bool knows(a, b) which tells you whether A knows B. Implement a functionint findCelebrity(n), your function should minimize the number of calls toknows. Note: There will be exactly one celebrity if he/she is in the party. Return the celebrity’s label if there is a celebrity in the party. If there is no celebrity, return-1.

Example 1: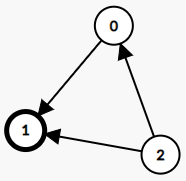

Input: graph = [
[1,1,0],
[0,1,0],
[1,1,1]
]
Output: 1
Explanation: There are three persons labeled with 0, 1 and 2. graph[i][j] = 1 means person i knows person j, otherwise graph[i][j] = 0 means person i does not know person j. The celebrity is the person labeled as 1 because both 0 and 2 know him but 1 does not know anybody.
Example 2: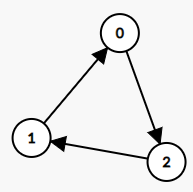

Input: graph = [
[1,0,1],
[1,1,0],
[0,1,1]
]
Output: -1
Explanation: There is no celebrity.

题解：
找名人，所有人都认识名人， 但名人不认识任何人
我们使用循环遍历候选人， 问A候选人， 你认识B吗？ 以后方式遍历整个数组，找到名人

我们使用一个一维数组来标记每各候选人的状态，如果 i 认识 j , 但是 j 不认识 i , 我们就暂时认为 j 是名人， 依次往下遍历，直到整个数组遍历完都没找到名人， 我们就认为 j 是名人
如果整个都没有出现的i 认识j ， j 不认识 i 的情况， 则没有名人， 范围 - 1

class Solution {
public int findCelebrity(int n) {

// 只看核心代码 ， 其他代码不完成，忽略， candidate[i]数组用来标记候选人状态
for (int i = 1; i < n; i++) {
for(int j = 0; i < n ; j++) {
if (candidate[i] && i != j) {
if (knows(i, j) || !knows(j, i)) {
candidate[i] = false;
break;
} else {
candidate[j] = false;
}
}
}
if (candidate[i]) return i;
}
return -1；
}
}