Diffusion Model
简介
diffusion model的思路是在$ T $步内对样本进行逐渐加噪声产生遵循特定分布(通常是高斯分布)以及通过网络学习逆向去除噪声来产生新样本。有三种设计Loss的思路,这里记录一下。
Denoising Diffusion Probabilistic Models (DDPMs)
[2006.11239] Denoising Diffusion Probabilistic Models (arxiv.org)
[1503.03585] Deep Unsupervised Learning using Nonequilibrium Thermodynamics (arxiv.org)

上面图的意思是,从右往左,给一张真实的图片逐渐加入噪声,当$ T \rightarrow \infty, \mathbf{x}T $完全成为一个遵从标准高斯分布$ \mathbf{x}_T \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) $的图片,每次加噪声的过程可以使用$ q(\mathbf{x}{t}|\mathbf{x}{t-1}) $来表示。从左往右看,每次去噪的过程可以通过$ q(\mathbf{x}{t-1}|\mathbf{x}{t}) $来表示。从右往左称为forward diffusion,从左往右则称为reverse diffusion。diffusion model的想法就是想得到求从右往左的过程,也就是想得到分布$ q(\mathbf{x}{t-1}|\mathbf{x}{t}) $,但是遗憾的$ q(\mathbf{x}{t-1}|\mathbf{x}{t}) $是未知的,所以diffusion model使用一个带参数$ \theta $的分布$ p\theta\left(\mathbf{x}{t-1} |\mathbf{x}_t\right) $来近似$ q(\mathbf{x}{t-1}|\mathbf{x}_{t}) $。
$ \begin{align}p\theta\left(\mathbf{x}{t-1} \mid \mathbf{x}t\right)=\mathcal{N}\left(\mathbf{x}{t-1} ; \boldsymbol{\mu}\theta\left(\mathbf{x}_t, t\right), \boldsymbol{\sigma}\theta\left(\mathbf{x}_t, t\right)\right)\end{align} $
其中$ \boldsymbol{\mu}\theta(\mathbf{x}{t},t) $是均值,$ \boldsymbol{\sigma}_\theta\left(\mathbf{x}_t, t\right) $是方差。
这个公式先放下不管,确认下我们的最终目标:让模型生成的样本点集合$ \mathbf{x}_{0} $的概率尽可能大,
量化一下就是使$ \log p\theta\left(\mathbf{x}_0\right) $尽可能大。很自然的就能想到使用最大似然估计(最大似然估计可以使这些数据在估计的分布中概率最大,一般使用$ \log $作为似然函数),这和VAE的思路接近。进一步来讲,VAE和Diffusion Model想找的都是一个对$ \log p\theta\left(\mathbf{x}0\right) $的最大似然估计,由于最大化似然估计可以转换成对$ -\log p\theta\left(\mathbf{x}0\right) $求最小值。虽然$ p\theta\left(\mathbf{x}_0\right) $分布未知,但是幸运的是以下公式成立:
$ \begin{align}\begin{split}-\log p\theta\left(\mathbf{x}_0\right) & \leq-\log p\theta\left(\mathbf{x}0\right)+D{\mathrm{KL}}\left(q\left(\mathbf{x}{1: T} \mid \mathbf{x}_0\right) | p\theta\left(\mathbf{x}{1: T} \mid \mathbf{x}_0\right)\right) \& =-\log p\theta\left(\mathbf{x}0\right)+\mathbb{E}{\mathbf{x}{1: T} \sim q\left(\mathbf{x}{1: T} \mid \mathbf{x}0\right)}\left[\log \frac{q\left(\mathbf{x}{1: T} \mid \mathbf{x}0\right)}{p\theta\left(\mathbf{x}{0: T}\right) / p\theta\left(\mathbf{x}0\right)}\right] \& =-\log p\theta\left(\mathbf{x}0\right)+\mathbb{E}_q\left[\log \frac{q\left(\mathbf{x}{1: T} \mid \mathbf{x}0\right)}{p\theta\left(\mathbf{x}{0: T}\right)}+\log p\theta\left(\mathbf{x}0\right)\right] \& =\mathbb{E}_q\left[\log \frac{q\left(\mathbf{x}{1: T} \mid \mathbf{x}0\right)}{p\theta\left(\mathbf{x}{0: T}\right)}\right] = L{VLB}\end{split}\end{align} $
由上面的公式可以看到负$ \log $似然的最大值是$ \mathbb{E}q\left[\log \frac{q\left(\mathbf{x}{1: T} \mid \mathbf{x}0\right)}{p\theta\left(\mathbf{x}{0: T}\right)}\right] $,所以为了求取负$ \log $似然的最小值,我们可以使它的最大值最小化。也就是我们的目标标成了求取$ \mathbb{E}_q\left[\log \frac{q\left(\mathbf{x}{1: T} \mid \mathbf{x}0\right)}{p\theta\left(\mathbf{x}_{0: T}\right)}\right] $的最小值。
由[1503.03585] Deep Unsupervised Learning using Nonequilibrium Thermodynamics (arxiv.org)中附录B的推导有:
$ \begin{align}\begin{split}& L{\mathrm{VLB}}=\mathbb{E}{q\left(\mathbf{x}{0: T}\right)}\left[\log \frac{q\left(\mathbf{x}{1: T} \mid \mathbf{x}0\right)}{p\theta\left(\mathbf{x}{0: T}\right)}\right] \& =\mathbb{E}_q\left[\log \frac{\prod{t=1}^T q\left(\mathbf{x}t \mid \mathbf{x}{t-1}\right)}{p\theta\left(\mathbf{x}_T\right) \prod{t=1}^T p\theta\left(\mathbf{x}{t-1} \mid \mathbf{x}t\right)}\right] \& =\mathbb{E}_q\left[-\log p\theta\left(\mathbf{x}T\right)+\sum{t=1}^T \log \frac{q\left(\mathbf{x}t \mid \mathbf{x}{t-1}\right)}{p\theta\left(\mathbf{x}{t-1} \mid \mathbf{x}t\right)}\right] \& =\mathbb{E}_q\left[-\log p\theta\left(\mathbf{x}T\right)+\sum{t=2}^T \log \frac{q\left(\mathbf{x}t \mid \mathbf{x}{t-1}\right)}{p\theta\left(\mathbf{x}{t-1} \mid \mathbf{x}t\right)}+\log \frac{q\left(\mathbf{x}_1 \mid \mathbf{x}_0\right)}{p\theta\left(\mathbf{x}0 \mid \mathbf{x}_1\right)}\right] \& =\mathbb{E}_q\left[-\log p\theta\left(\mathbf{x}T\right)+\sum{t=2}^T \log \left(\frac{q\left(\mathbf{x}{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)}{p\theta\left(\mathbf{x}{t-1} \mid \mathbf{x}_t\right)} \cdot \frac{q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)}{q\left(\mathbf{x}{t-1} \mid \mathbf{x}0\right)}\right)+\log \frac{q\left(\mathbf{x}_1 \mid \mathbf{x}_0\right)}{p\theta\left(\mathbf{x}0 \mid \mathbf{x}_1\right)}\right] \& =\mathbb{E}_q\left[-\log p\theta\left(\mathbf{x}T\right)+\sum{t=2}^T \log \frac{q\left(\mathbf{x}{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)}{p\theta\left(\mathbf{x}{t-1} \mid \mathbf{x}_t\right)}+\sum{t=2}^T \log \frac{q\left(\mathbf{x}t \mid \mathbf{x}_0\right)}{q\left(\mathbf{x}{t-1} \mid \mathbf{x}0\right)}+\log \frac{q\left(\mathbf{x}_1 \mid \mathbf{x}_0\right)}{p\theta\left(\mathbf{x}0 \mid \mathbf{x}_1\right)}\right] \& =\mathbb{E}_q\left[-\log p\theta\left(\mathbf{x}T\right)+\sum{t=2}^T \log \frac{q\left(\mathbf{x}{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)}{p\theta\left(\mathbf{x}{t-1} \mid \mathbf{x}_t\right)}+\log \frac{q\left(\mathbf{x}_T \mid \mathbf{x}_0\right)}{q\left(\mathbf{x}_1 \mid \mathbf{x}_0\right)}+\log \frac{q\left(\mathbf{x}_1 \mid \mathbf{x}_0\right)}{p\theta\left(\mathbf{x}0 \mid \mathbf{x}_1\right)}\right] \& =\mathbb{E}_q\left[\log \frac{q\left(\mathbf{x}_T \mid \mathbf{x}_0\right)}{p\theta\left(\mathbf{x}T\right)}+\sum{t=2}^T \log \frac{q\left(\mathbf{x}{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)}{p\theta\left(\mathbf{x}{t-1} \mid \mathbf{x}_t\right)}-\log p\theta\left(\mathbf{x}0 \mid \mathbf{x}_1\right)\right] \& =\mathbb{E}_q[\underbrace{D{\mathrm{KL}}\left(q\left(\mathbf{x}T \mid \mathbf{x}_0\right) | p\theta\left(\mathbf{x}T\right)\right)}{LT}+\sum{t=2}^T \underbrace{D{\mathrm{KL}}\left(q\left(\mathbf{x}{t-1} \mid \mathbf{x}t, \mathbf{x}_0\right) | p\theta\left(\mathbf{x}{t-1} \mid \mathbf{x}_t\right)\right)}{L{t-1}}-\underbrace{\log p\theta\left(\mathbf{x}0 \mid \mathbf{x}_1\right)}{L_{0}}] \&\end{split}\end{align} $
继续展开则有:
$ \begin{align}\begin{split}L{\mathrm{VLB}} & =L_T+L{T-1}+\cdots+L0 \\text { where } L_T & =D{\mathrm{KL}}\left(q\left(\mathbf{x}T \mid \mathbf{x}_0\right) | p\theta\left(\mathbf{x}T\right)\right) \L_t & =D{\mathrm{KL}}\left(q\left(\mathbf{x}t \mid \mathbf{x}{t+1}, \mathbf{x}0\right) | p\theta\left(\mathbf{x}t \mid \mathbf{x}{t+1}\right)\right) \text { for } 1 \leq t \leq T-1 \L0 & =-\log p\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)\end{split}\end{align} $
其中$ q\left(\mathbf{x}t \mid \mathbf{x}{t+1}, \mathbf{x}0\right) $表示在$ \mathbf{x}{0} $和$ \mathbf{x}{t+1} $两个条件下$ \mathbf{x}{t} $的概率。至此,我们的目标就变成了如何求上面的每一项$ {KL} $散度。注意上面提到过,当$ T \rightarrow \infty $,$ \mathbf{x}T $遵从标准高斯分布$ \mathbf{x}_T \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) $。所以$ p\theta\left(\mathbf{x}T\right) $是标准正态分布,没有可学习的参数,在训练过程中可以忽略。$ L{0} $的在[2006.11239] Denoising Diffusion Probabilistic Models (arxiv.org)这篇文章中有提到过使用decoder去建模,先略过,下面我们先关注对$ L_{t} $的建模方法。
为了计算$ L{t} $,根据公式$ (1) $可以知道$ p{\theta}(\mathbf{x}{t}|\mathbf{x}{t+1}) $的形式,接下来我们推导$ q\left(\mathbf{x}t \mid \mathbf{x}{t+1}, \mathbf{x}_0\right) $,由贝叶斯公式有:
$ \begin{equation}q\left(\mathbf{x}{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)=q\left(\mathbf{x}_t \mid \mathbf{x}{t-1}, \mathbf{x}0\right) \frac{q\left(\mathbf{x}{t-1} \mid \mathbf{x}_0\right)}{q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)}\end{equation} $
为了求上面公式中的每一项,回过头来看forward diffusion。forward diffusion是一个不断往结果上加噪声的过程。用数学语言表达就是:
$ \begin{equation} \mathbf{x}t \sim q\left(\mathbf{x}_t \mid \mathbf{x}{t-1}\right)=\mathcal{N}\left(\mathbf{x}t ; \sqrt{1-\beta_t} \mathbf{x}{t-1}, \beta_t \mathbf{I}\right) \end{equation} $
其中$ \beta{t} $是控制噪声的强度的参数。让$ \alpha_t=1-\beta_t $,$ \bar{\alpha}_t=\prod{i=1}^t \alpha_i $使用重参数化技巧可以得到:
$ \begin{align}\begin{array}{rlr}\mathbf{x}t & =\sqrt{\alpha_t} \mathbf{x}{t-1}+\sqrt{1-\alphat} \boldsymbol{\epsilon}{t-1} & \quad ; \text { where } \boldsymbol{\epsilon}{t-1}, \boldsymbol{\epsilon}{t-2}, \cdots \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \& =\sqrt{\alphat \alpha{t-1}} \mathbf{x}{t-2}+\sqrt{1-\alpha_t \alpha{t-1}} \overline{\boldsymbol{\epsilon}}{t-2} & ; \text { where } \overline{\boldsymbol{\epsilon}}{t-2} \text { merges two Gaussians (*). } \& =\ldots & \& =\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t}\boldsymbol{\epsilon} \q\left(\mathbf{x}_t \mid \mathbf{x}_0\right) & =\mathcal{N}\left(\mathbf{x}_t ; \sqrt{\bar{\alpha}_t} \mathbf{x}_0,\left(1-\bar{\alpha}_t\right) \mathbf{I}\right) &\end{array}\end{align} $
上面公式第一行表示的是已知$ \mathbf{x}{t-1} $时$ \mathbf{x}{t} $的概率分布。由于$ \mathbf{x}{0} $已知,所以表示的就是$ q\left(\mathbf{x}_t \mid \mathbf{x}{t-1}, \mathbf{x}0\right) $ 。又已知$ \mathbf{x}{t}= \sqrt{\bar{\alpha}t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t}\boldsymbol{\epsilon} $,则$ \mathbf{x}{t-1}= \sqrt{\bar{\alpha}{t-1}} \mathbf{x}_0+\sqrt{1-\bar{\alpha}{t-1}}\boldsymbol{\epsilon} $,即可知$ q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_0\right) $。由$ \mathbf{x} \sim N(\mu. \sigma^{2})\propto \mathbf{x} = \mu + \sigma \epsilon $可知:
$ \begin{equation}\begin{aligned}q\left(\mathbf{x}t \mid \mathbf{x}{t-1}, \mathbf{x}0\right)=\sqrt{\alpha_t} x{t-1}+\sqrt{1-\alphat} z \quad \sim \mathcal{N}\left(\sqrt{\alpha_t} x{t-1}, (1-\alphat)\mathbf{I}\right)\ q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)=\sqrt{\bar{\alpha}_t} x_0+\sqrt{1-\bar{\alpha}_t} z \quad \sim \mathcal{N}\left(\sqrt{\bar{\alpha}_t} x_0, (1-\bar{\alpha}_t)\mathbf{I}\right)\q\left(\mathbf{x}{t-1} \mid \mathbf{x}0\right)=\sqrt{\bar{\alpha}{t-1}} x0+\sqrt{1-\bar{a}{t-1}} z \quad \sim \mathcal{N}\left(\sqrt{\bar{\alpha}{t-1}} x_0, (1-\bar{\alpha}{t-1})\mathbf{I}\right)\end{aligned}\end{equation} $
高斯分布乘除高斯分布后还是高斯分布,因此有:
$ \begin{align}q(\mathbf{x}{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) &= \mathcal{N}(\mathbf{x}{t-1}; {\tilde{\boldsymbol{\mu}}}(\mathbf{x}_t, \mathbf{x}_0), {\tilde{\sigma}^{2}_t} \mathbf{I}) \
q(\mathbf{x}{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) &= q(\mathbf{x}_t \vert \mathbf{x}{t-1}, \mathbf{x}0) \frac{ q(\mathbf{x}{t-1} \vert \mathbf{x}0) }{ q(\mathbf{x}_t \vert \mathbf{x}_0) } \ &\propto \exp \Big(-\frac{1}{2} \big(\frac{(\mathbf{x}_t - \sqrt{\alpha_t} \mathbf{x}{t-1})^2}{\betat} + \frac{(\mathbf{x}{t-1} - \sqrt{\bar{\alpha}{t-1}} \mathbf{x}_0)^2}{1-\bar{\alpha}{t-1}} - \frac{(\mathbf{x}t - \sqrt{\bar{\alpha}_t} \mathbf{x}_0)^2}{1-\bar{\alpha}_t} \big) \Big) \ &= \exp \Big(-\frac{1}{2} \big(\frac{\mathbf{x}_t^2 - 2\sqrt{\alpha_t} \mathbf{x}_t {\mathbf{x}{t-1}} {+ \alphat} {\mathbf{x}{t-1}^2} }{\betat} + \frac{ {\mathbf{x}{t-1}^2} {- 2 \sqrt{\bar{\alpha}{t-1}} \mathbf{x}_0} {\mathbf{x}{t-1}}{+ \bar{\alpha}{t-1} \mathbf{x}_0^2} }{1-\bar{\alpha}{t-1}} - \frac{(\mathbf{x}t - \sqrt{\bar{\alpha}_t} \mathbf{x}_0)^2}{1-\bar{\alpha}_t} \big) \Big) \ &= \exp\Big( -\frac{1}{2} \big( {(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}{t-1}})} \mathbf{x}{t-1}^2 -{(\frac{2\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{2\sqrt{\bar{\alpha}{t-1}}}{1 - \bar{\alpha}{t-1}} \mathbf{x}_0)} \mathbf{x}{t-1} { + C(\mathbf{x}_t, \mathbf{x}_0) \big) \Big)} \end{align} $
其中$ C(\mathbf{x}{t},\mathbf{x}{0}) $是与求取高斯分布均值和方差无关的项,因此省略。对一般的高斯分布展开可以看到:
$ \begin{align}\exp \left(-\frac{(x-\mu)^2}{2 \sigma^2}\right)=\exp \left(-\frac{1}{2}\left(\frac{1}{\sigma^2} x^2-\frac{2 \mu}{\sigma^2} x+\frac{\mu^2}{\sigma^2}\right)\right)=\exp \left(-\frac{1}{2}\left(A x^2-B x+C\right)\right)\end{align} $
因此:
$ \begin{align} \tilde{\sigma}^{2}t &= 1/(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}{t-1}}) = 1/(\frac{\alphat - \bar{\alpha}_t + \beta_t}{\beta_t(1 - \bar{\alpha}{t-1})}) = {\frac{1 - \bar{\alpha}{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t} \ \tilde{\boldsymbol{\mu}}_t (\mathbf{x}_t, \mathbf{x}_0) &= (\frac{\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}{t-1} }}{1 - \bar{\alpha}{t-1}} \mathbf{x}_0)/(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}{t-1}}) \ &= (\frac{\sqrt{\alphat}}{\beta_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}{t-1} }}{1 - \bar{\alpha}{t-1}} \mathbf{x}_0) {\frac{1 - \bar{\alpha}{t-1}}{1 - \bar{\alpha}t} \cdot \beta_t} \ &= \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}{t-1})}{1 - \bar{\alpha}t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}{t-1}}\beta_t}{1 - \bar{\alpha}_t} \mathbf{x}_0\ \end{align} $
上面的均值公式中有$ \mathbf{x}{0} $,但是$ \mathbf{x}{0} $是未知的。但是由公式$ (7) $可以得到$ \mathbf{x}_0=\frac{1}{\sqrt{\bar{\alpha}_t}}\left(\mathbf{x}_t-\sqrt{1-\bar{\alpha}_t} \epsilon_t\right) $,因此:
$ \begin{align} \tilde{\boldsymbol{\mu}}t &= \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}{t-1})}{1 - \bar{\alpha}t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}{t-1}}\beta_t}{1 - \bar{\alpha}_t} \frac{1}{\sqrt{\bar{\alpha}_t}}(\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t) \ &= {\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big)} \end{align} $
到此为止我们就求出了$ q(\mathbf{x}{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) $的高斯分布形式,由于$ \sigma^{2} $只与$ \beta{t} $有关($ \bar{\alpha}{t} $也只与$ \beta{t} $有关),$ \beta_{t} $是预先知道的量,所以我们仅需要近似$ \tilde{\mu} $即可。
对于$ p\theta\left(\mathbf{x}{t-1} \mid \mathbf{x}t\right)=\mathcal{N}\left(\mathbf{x}{t-1} ; \boldsymbol{\mu}\theta\left(\mathbf{x}_t, t\right), \boldsymbol{\sigma}\theta\left(\mathbf{x}t, t\right)\right) $,我们想去近似$ q(\mathbf{x}{t-1} \vert \mathbf{x}t, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}{t-1}; {\tilde{\boldsymbol{\mu}}}(\mathbf{x}t, \mathbf{x}_0), {\tilde{\sigma}^{2}_t} \mathbf{I}) $,由于$ \tilde{\boldsymbol{\mu}}_t = \frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big) $,$ \mathbf{x}{t} $在训练时是已知的,所以我们可以重新表示$ p\theta\left(\mathbf{x}{t-1} \mid \mathbf{x}t\right) $的均值(前面提到方差当$ \beta{t} $确定时已知,所以只处理均值),有:
$ \begin{align}\boldsymbol{\mu}\theta\left(\mathbf{x}_t, t\right)&=\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}\theta\left(\mathbf{x}t, t\right)\right) \ \mathbf{x}{t-1}&\sim\mathcal{N}\left(\mathbf{x}{t-1} ; \frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}\theta\left(\mathbf{x}t, t\right)\right), \boldsymbol{\sigma}\theta\left(\mathbf{x}_t, t\right)\right)\end{align} $
由于参与$ KL $散度计算的两个分布都是高斯分布,所以可以使用KL Divergence between 2 Gaussian Distributions (mr-easy.github.io)中的计算公式。如果只考虑均值(方差不变),
$ \begin{align}Lt&=D{\mathrm{KL}}\left(q\left(\mathbf{x}t \mid \mathbf{x}{t+1}, \mathbf{x}0\right) | p\theta\left(\mathbf{x}t \mid \mathbf{x}{t+1}\right)\right) D{K L}(p | q) \ &=\frac{1}{2}\left[\log \frac{\left|\sigma_q\right|}{\left|\sigma_p\right|}-k+\left(\boldsymbol{\mu}{\boldsymbol{p}}-\boldsymbol{\mu}{\boldsymbol{q}}\right)^T \sigma_q^{-1}\left(\boldsymbol{\mu}{\boldsymbol{p}}-\boldsymbol{\mu}_{\boldsymbol{q}}\right)+\operatorname{tr}\left{\sigma_q^{-1} \sigma_p\right}\right]\end{align} $
便是可以计算的了,有:
$ \begin{align}Lt &= \mathbb{E}{\mathbf{x}0, \boldsymbol{\epsilon}} \Big[\frac{1}{2 | \boldsymbol{\sigma}\theta(\mathbf{x}t, t) |^2_2} | \color{red}{\tilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0)} - \color{green}{\boldsymbol{\mu}\theta(\mathbf{x}t, t)} |^2 \Big] \&= \mathbb{E}{\mathbf{x}0, \boldsymbol{\epsilon}} \Big[\frac{1}{2 |\boldsymbol{\sigma}\theta |^22} | \color{red}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big)} - \color{green}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\boldsymbol{\epsilon}}\theta(\mathbf{x}t, t) \Big)} |^2 \Big] \&= \mathbb{E}{\mathbf{x}0, \boldsymbol{\epsilon}} \Big[\frac{ (1 - \alpha_t)^2 }{2 \alpha_t (1 - \bar{\alpha}_t) | \boldsymbol{\sigma}\theta |^22} |\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}\theta(\mathbf{x}t, t)|^2 \Big] \&= \mathbb{E}{\mathbf{x}0, \boldsymbol{\epsilon}} \Big[\frac{ (1 - \alpha_t)^2 }{2 \alpha_t (1 - \bar{\alpha}_t) | \boldsymbol{\sigma}\theta |^22} |\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t, t)|^2 \Big] \end{align} $
去掉系数项简化一下效果会更好([2006.11239] Denoising Diffusion Probabilistic Models (arxiv.org)),可以得到最终的目标函数为:
$ \begin{align}Lt^\text{simple}&= \mathbb{E}{t \sim [1, T], \mathbf{x}0, \boldsymbol{\epsilon}_t} \Big[|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}\theta(\mathbf{x}t, t)|^2 \Big] \&= \mathbb{E}{t \sim [1, T], \mathbf{x}0, \boldsymbol{\epsilon}_t} \Big[|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t, t)|^2 \Big]\end{align} $
有了目标函数,自然得到训练过程。推理过程像前面说的是一样是一个去噪过程,由于$ \mathbf{x}_{t-1} $的分布形式如公式$ (22) $所示,所以通过标准正常分布重参数化可以得到推理过程如下所示:


Score-Based Generative Models (SGMs)
[1907.05600] Generative Modeling by Estimating Gradients of the Data Distribution (arxiv.org)
[2006.09011] Improved Techniques for Training Score-Based Generative Models (arxiv.org)
这类方法的基本想法来源于Score Matching和Langevin Dynamics
(ref: Andy Jones (andrewcharlesjones.github.io))。Score Matching的思路是估计概率密度函数$ p{data}(\mathbf{x}) $的梯度$ \nabla_x \log p{data}(\mathbf{x}) $,而不是直接估计概率密度函数本身。这种方法本身被用于解决最大似然中某些概率密度函数不可归一化的问题(参考上面的引用),最终的目标函数如下:
$ \begin{equation}\frac{1}{2} \mathbb{E}{p{\text {data }}}\left[\left|\mathbf{s}{\boldsymbol{\theta}}(\mathbf{x})-\nabla{\mathbf{x}} \log p_{\text {data }}(\mathbf{x})\right|_2^2\right]\end{equation} $
其中$ \mathbf{s}{\theta}(\mathbf{x}) $表示Score Function。实际上就是对最大似然梯度$ \nabla_x \log p{data}(\mathbf{x}) $的近似。进一步推导有:
$ \begin{equation}\mathbb{E}{p{\text {data }}(x)}\left[\operatorname{tr}\left(\nabla{\mathbf{x}} s{\boldsymbol{\theta}}(\mathbf{x})\right)+\frac{1}{2}\left|s_{\boldsymbol{\theta}}(\mathbf{x})\right|_2^2\right]\end{equation} $
Langevin Dynamics则可以通过概率密度函数的梯度 $ \nabla_x \log p(x ; \theta) $以及标准正态分布$ \mathbf{z}_t \sim \mathcal{N}(0, I) $和生成样本:
$ \begin{equation} \tilde{\mathbf{x}}t=\tilde{\mathbf{x}}{t-1}+\frac{\epsilon}{2} \nabla{\mathbf{x}} \log p\left(\tilde{\mathbf{x}}{t-1}\right)+\sqrt{\epsilon} \mathbf{z}_t \end{equation} $
有了这两样数学工具,直接的想法是直接利用Score Matching学习样本,然后使用Langevin Dynamics产生新的样本。但是Score Matching中的$ \operatorname{tr}\left(\nabla{\mathbf{x}}p{\theta}(\mathbf{x})\right) $ 不能直接被用于深度学习中(由于计算这一项会非常复杂而且性能不可接受),所以一般会使用Denoising Score Matching(smdae_techreport.pdf (umontreal.ca))和Sliced Score Matching([1905.07088] Sliced Score Matching: A Scalable Approach to Density and Score Estimation (arxiv.org))两种适用于深度学习的方法。使用网络代替Score Function $ \mathbf{s}_{\theta}(\mathbf{x}) $:
Denoising Score Matching的目标函数如下:
$ \begin{equation}\frac{1}{2} \mathbb{E}{q\sigma(\tilde{\mathbf{x}} \mid \mathbf{x}) p{\text {data }}(\mathbf{x})}\left[\left|\mathbf{s}{\boldsymbol{\theta}}(\tilde{\mathbf{x}})-\nabla{\tilde{\mathbf{x}}} \log q\sigma(\tilde{\mathbf{x}} \mid \mathbf{x})\right|_2^2\right]\end{equation} $
其中$ \tilde{\mathbf{x}} $ $ \tilde{\mathbf{x}} $$ q\sigma(\tilde{\mathbf{x}} \mid \mathbf{x}) $是预定义的噪声函数分布,也就是将对$ \nabla_x \log p{data}(x) $的估计变成了对噪声函数梯度的估计。
Sliced Score Matching的目标函数如下:
$ \begin{equation}\mathbb{E}{p{\mathbf{v}}} \mathbb{E}{p{\text {data }}}\left[\mathbf{v}^{\top} \nabla{\mathbf{x}} \mathbf{s}{\boldsymbol{\theta}}(\mathbf{x}) \mathbf{v}+\frac{1}{2}\left|\mathbf{p}_{\boldsymbol{\theta}}(\mathbf{x})\right|_2^2\right]\end{equation} $
其中$ p_{\mathbf{v}} $是一个简单的随机分布,比如标准正态分布。
还需要注意的是Score Macthing只有当数据集能够覆盖整个空间时,才能给出一致估计。然而流型理论则认为真实世界的数据倾向于处于高维空间的一个低维嵌入空间中(Ambient Space)。另外由于$ \mathbf{x} $聚集在低维空间中,对$ \nabla{\mathbf{x}} \log p{\text {data }}(\mathbf{x}) $实际上未定义(因为$ \mathbf{x} $ 不能铺满整个函数的定义域,没法求梯度)。直接使用这两样工具的后果是网络并不会收敛。
为了解决这个问题,观察到高斯噪声遍布整个空间(想象一下一维的情况),而大的高斯噪声(高斯分布靠近0的部分,也靠近低维数据)会对低维数据产生更强的扰动。所以在数据上加上高斯噪声可以解决上面的两个问题。那么自然而然的,SGMs需要使用Denoising Score Matching。
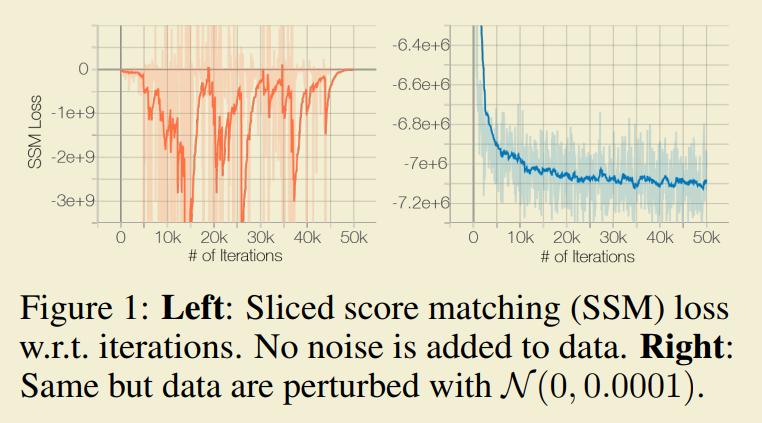
另一个问题是Langevin Dynamics在处理多数据分布(多种分布形式的组合)混合时即会产生错误的分布估计,采样收敛效率也不高。
SGMs通过在数据上加上不同扰动水平的高斯分布让网络来估计模型,在采样时先使用大噪声产生初始样本,然后使用小噪声迭代产生新样本的方法产生新的数据加快采样收敛过程(这个过程与模拟退火的想法类型)。可以看到退火+Langevin Dynamics在估计多数据分布组成的样本时有更好的效果。
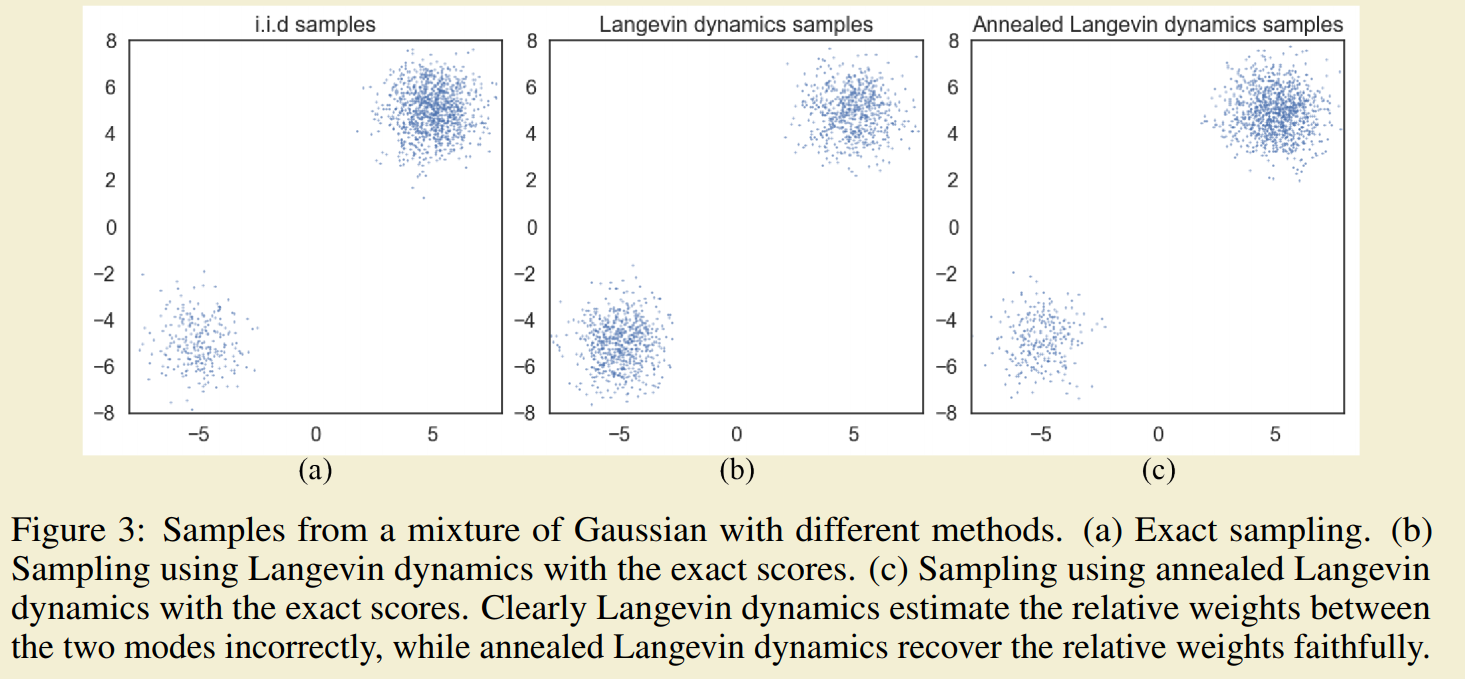
选用$ q\sigma(\tilde{\mathbf{x}} \mid \mathbf{x})=\mathcal{N}\left(\tilde{\mathbf{x}} \mid \mathbf{x}, \sigma^2 I\right) $作为先验的噪声分布且$ \nabla{\tilde{\mathbf{x}}} \log q_\sigma(\tilde{\mathbf{x}} \mid \mathbf{x})=-(\tilde{\mathbf{x}}-\mathbf{x}) / \sigma^2 $,最终的目标函数如下:
$ \begin{equation}\mathcal{L}\left(\boldsymbol{\theta} ;\left{\sigmai\right}{i=1}^L\right) \triangleq \frac{1}{L} \sum{i=1}^L \lambda\left(\sigma_i\right) \ell\left(\boldsymbol{\theta} ; \sigma_i\right)\end{equation} $$ \begin{equation}\ell(\boldsymbol{\theta} ; \sigma) \triangleq \frac{1}{2} \mathbb{E}{p{\text {data }}(\mathbf{x})} \mathbb{E}{\tilde{\mathbf{x}} \sim \mathcal{N}\left(\mathbf{x}, \sigma^2 I\right)}\left[\left|\mathbf{s}_{\boldsymbol{\theta}}(\tilde{\mathbf{x}}, \sigma)+\frac{\tilde{\mathbf{x}}-\mathbf{x}}{\sigma^2}\right|_2^2\right]\end{equation} $
采样过程如下:

SGMs本质和DDPM是一致的,它们都是通过在样本上增加噪声然后学习去噪来生成样本。但是它们设计Loss的出发点有些不同,SGMs是通过近似Score Function,DDPM则是近似后验概率分布$ q(\mathbf{x}{t-1}|\mathbf{x}{t}) $。
Stochastic Differential Equations (Score SDEs)
[2011.13456] Score-Based Generative Modeling through Stochastic Differential Equations (arxiv.org)
Markov chain Monte Carlo - Wikipedia
Probability current / Probability flow - Wikipedia
加噪去噪的SDE表示
Diffusion Model的核心是加噪和去噪。数学化表达一下就是:
初始数据集是$ \mathbf{x}(0) $,初始数据集的分布为$ \mathbf{x}(0) \sim p0 $;最终加噪后的数据集是$ \mathbf{x}(T) $,最终样本数据集的分布是$ \mathbf{x}(T) \sim p_T $,通常是某种先验的分布,比如高斯分布。diffusion过程表示为$ {\mathbf{x}(t)}{t=0}^T,t \in [0, T] $,
Score SDE是DDPM和SGMs的时间连续形式。Score SDE认为Diffusion Model中的加噪声过程可以通过以下随机微分方程(SDE)表示:
$ \begin{equation}\mathrm{d} \mathbf{x}=\mathbf{f}(\mathbf{x}, t) \mathrm{d} t+g(t) \mathrm{d} \mathbf{w}\end{equation} $
其中$ \mathbf{w} $表示时间从0到$ T $的标准维纳过程(比如布朗运动)。$ \mathbf{f}(\cdot, t): \mathbb{R}^d \rightarrow \mathbb{R}^d $是一个向量值函数,作为$ \mathbf{x}(t) $的漂移(drift)系数。$ g(\cdot): \mathbb{R} \rightarrow \mathbb{R} $是一个标量值函数,作为$ \mathbf{x}(t) $的扩散(diffusion)系数。这个随机微分方程在$ \mathbf{x} $和$ t $连续的时候有唯一的强形式解。另一方面,Score SDE认为Diffusion Model中的去噪声过程可以用过一下随机微分方程表示:
$ \begin{equation}\mathrm{d} \mathbf{x}=\left[\mathbf{f}(\mathbf{x}, t)-g(t)^2 \nabla_{\mathbf{x}} \log p_t(\mathbf{x})\right] \mathrm{d} t+g(t) \mathrm{d} \overline{\mathbf{w}}\end{equation} $
其中$ \overline{\mathbf{w}} $表示时间从$ T $到0的标准维纳过程,其他符合与上面公式相同。从这个SDE可以看出如果我们已知$ \nabla{\mathbf{x}} \log p_t(\mathbf{x}) $,那么按照这个SDE去处理,就可以从$ p{0} $分布中得到正确的采样。
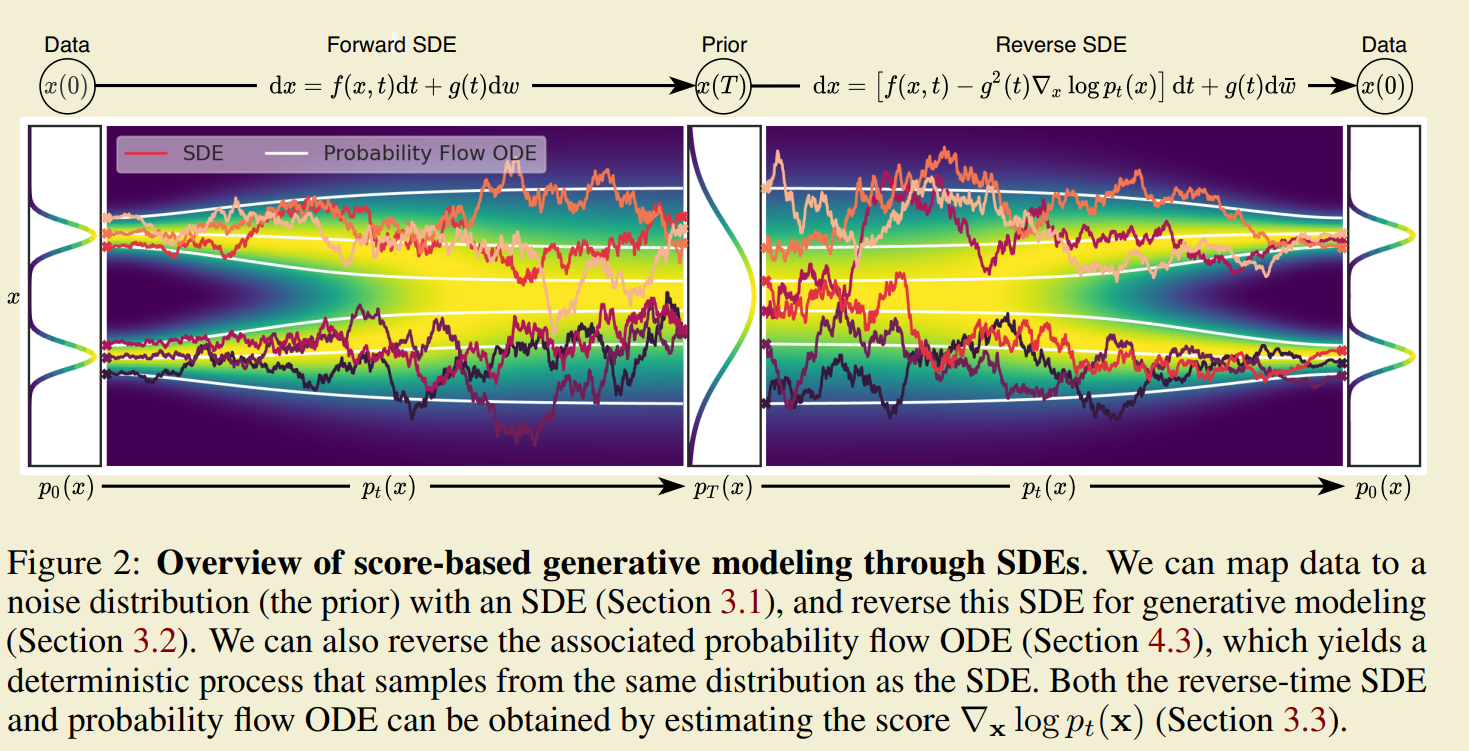
对Score进行估计
为了得到$ \nabla_{\mathbf{x}} \log p_t(\mathbf{x}) $,可以沿用SGMs的思路使用Denosing Score Matching来估计,对于连续形式的SDE,我们可以用以下连续形式的目标函数:
$ \begin{equation}\boldsymbol{\theta}^*=\underset{\boldsymbol{\theta}}{\arg \min } \mathbb{E}t\left{\lambda(t) \mathbb{E}{\mathbf{x}(0)} \mathbb{E}{\mathbf{x}(t) \mid \mathbf{x}(0)}\left[\left|\mathbf{s}{\boldsymbol{\theta}}(\mathbf{x}(t), t)-\nabla{\mathbf{x}(t)} \log p{0 t}(\mathbf{x}(t) \mid \mathbf{x}(0))\right|_2^2\right]\right}\end{equation} $
其中$ p{0 t}(\mathbf{x}(t) \mid \mathbf{x}(0)) $表示从$ \mathbf{x}(0) $到$ \mathbf{x}(t) $的transition kernel 。 $ \lambda(t) $是权重函数,仿照DDPM和SGMs,可以选用$ \lambda \propto 1 / \mathbb{E}\left[\left|\nabla{\mathbf{x}(t)} \log p_{0 t}(\mathbf{x}(t) \mid \mathbf{x}(0))\right|_2^2\right] $。如果$ \mathbf{f}(\cdot, t) $是仿射变换,那么transition kernel一般是高斯分布(比如DDPM,参考(8)式,SGMs的这部分也满足仿射变换,所以也是高斯分布)。如果$ \mathbf{f}(\cdot, t) $不是仿射变换,则需要解Kolmogorov’s forward equation 来获取transition kernel 。
与DDPM和SGMs的联系
上面提到过Score SDE是DDPM和SGMs的时间连续形式。对于DDPM,加噪声过程的离散马尔科夫链表示为:
$ \begin{equation}\mathbf{x}i=\sqrt{1-\beta_i} \mathbf{x}{i-1}+\sqrt{\betai} \mathbf{z}{i-1}, \quad i=1, \cdots, N\end{equation} $
当$ N \rightarrow \infty $,(41)收敛到SDE:
$ \begin{equation}\mathrm{d} \mathbf{x}=-\frac{1}{2} \beta(t) \mathbf{x} \mathrm{d} t+\sqrt{\beta(t)} \mathrm{d} \mathbf{w}\end{equation} $
对于SGMs,有离散的马尔科夫链为:
$ \begin{equation}\mathbf{x}i=\mathbf{x}{i-1}+\sqrt{\sigmai^2-\sigma{i-1}^2} \mathbf{z}_{i-1}, \quad i=1, \cdots, N\end{equation} $
当$ N \rightarrow \infty $,(42)收敛到SDE:
$ \begin{equation}\mathrm{d} \mathbf{x}=\sqrt{\frac{\mathrm{d}\left[\sigma^2(t)\right]}{\mathrm{d} t}} \mathrm{~d} \mathbf{w}\end{equation} $
他们都满足公式(38)的形式。
如何解去噪的SDE(采样)
- 通用数值解算器
- 直接使用Euler-Maruyama 或者stochastic Runge-Kutta methods 之类的数值解法去解算SDE,或者使用[2011.13456] Score-Based Generative Modeling through Stochastic Differential Equations (arxiv.org)中附录$ E $提出的方法。
- 预测-修正采样器
- 这种采样的思路是使用通用数值解算器作为预测器先产生一个结果,然后使用score-based MCMC (Markov Chain Monte Carlo)作为修正器。交织进行可以加速采样效率(实际上也是加速解SDE的过程)
带条件的Diffusion Model (Guided Diffusion Model)
通俗理解Classifier Guidance 和 Classifier-Free Guidance 的扩散模型 - 知乎 (zhihu.com)
考虑带有条件$ y $的数据分布$ p(x\mid y) $,使用我们SGM Diffusion推导,我们的目标是求取$ \nabla_x \log p(x \mid y) $,由贝叶斯公式有:
$ \begin{equation}\begin{gathered}p(x \mid y)=\frac{p(y \mid x) \cdot p(x)}{p(y)} \\Longrightarrow \log p(x \mid y)=\log p(y \mid x)+\log p(x)-\log p(y) \\Longrightarrow \nabla_x \log p(x \mid y)=\nabla_x \log p(y \mid x)+\nabla_x \log p(x),\end{gathered}\end{equation} $
这个公式说明我们要求的有条件Score Function$ \nabla_x \log p(x \mid y) $可以通过无条件Score Function $ \nabla_x \log p(x) $和条件项 $ \nabla_x \log p(y \mid x) $(这一项不是Score Function,因为不是对$ y $求的梯度,只能算是个条件)加和得到。
使用分类器
[2105.05233] Diffusion Models Beat GANs on Image Synthesis (arxiv.org)
观察到$ (46) $式中的$ p(y\mid x) $实际上是一个分类器,简单的想法就是再让一个网络学习一个分类器即可:
$ \begin{equation}\nablax \log p\gamma(x \mid y)=\nabla_x \log p(x)+\gamma \nabla_x \log p(y \mid x)\end{equation} $
其中$ \gamma $是guidance scale,表示对条件的方法因子,这个值$ >1 $且越大,条件的影响越强,否则越弱。
但是这种方法一是要多训练一个分类器,二是使用梯度更新图像会导致对抗攻击效应,生成器可能会通过人眼不可察觉的细节来欺骗分配器,实际上没有按照条件生成。
Classifier-free Guidance
Guidance: a cheat code for diffusion models – Sander Dieleman
这种方式顾名思义是不使用额外的分类器,它的基本想法是通过随机丢弃条件(大约$ 10 - 20 \% $)来在一个网络中同时训练有条件项和无条件项(丢弃条件信息时往往用一个特定值来代替)。这个网络同时学习了有条件项(分类器)和无条件项,注意到对于分类器有公式$ (47) $成立,另外有:
$ \begin{equation}\begin{gathered}p(y \mid x)=\frac{p(x \mid y) \cdot p(y)}{p(x)} \\Longrightarrow \log p(y \mid x)=\log p(x \mid y)+\log p(y)-\log p(x) \\Longrightarrow \nabla_x \log p(y \mid x)=\nabla_x \log p(x \mid y)-\nabla_x \log p(x) .\end{gathered}\end{equation} $
将$ (48) $带入$ (47) $中有:
$ \begin{align}\begin{split}\nablax \log p\gamma(x \mid y)&=\nabla_x \log p(x)+\gamma\left(\nabla_x \log p(x \mid y)-\nabla_x \log p(x)\right) \ &=(1-\gamma) \nabla_x \log p(x)+\gamma \nabla_x \log p(x \mid y)\end{split}\end{align} $
其中$ \gamma $是仍然是guidance scale,如果$ \gamma $是$ 0 $,则表示标准无条件模型。如果$ \gamma $是$ 1 $,则表示标准有条件模型,如果$ \gamma > 1 $,则条件继续增强,获得神奇的结果。如下图所示(OpenAI GLIDE):

实现
一系列Diffusion模型的实现
一个Denoising Diffusion模型的实现,里面技巧和参考文章比较多,看了上面的再看这个实现比较合适
很多深度学习paper的实现,涉及了很多经典文章
Reference
diffusion model的详细推导,主要就是参考这篇文章理的思路,中间有些推导有些莫明奇妙,参考下一篇一起看比较合适。
这篇文章补充了很多上文没有的详细推导,适合和上一篇一次看。
hugging face 提供的diffusion model的介绍课程,第一课对diffusion Model进行了详细的介绍,还有代码实现和其他文章的引用。
Diffusion Model的简介。主要是代码的实现,原理还是多看上面的文章比较合适。
22年对Diffusion Model的一个综述,对那时候主流的Diffusion方法简单介绍并说了下diffusion在采样加速、提升更准确的最大似然估计以及应用到特殊数据结构的进展,综述的最后还提供了一些应用的例子。
对Score Matching的解释,对学习SGMs有帮助。
关于Diffusion Guidance很好的一篇介绍文章。


