k-means 算法是一种基于划分的聚类算法,它以 k 为参数,把 n 个数据对象分成 k 个簇,使簇内具有较高的相似度,而簇间的相似度较低。
1. 基本思想
k-means 算法是根据给定的 n 个数据对象的数据集,构建 k 个划分聚类的方法,每个划分聚类即为一个簇。该方法将数据划分为 n 个簇,每个簇至少有一个数据对象,每个数据对象必须属于而且只能属于一个簇。同时要满足同一簇中的数据对象相似度高,不同簇中的数据对象相似度较小。聚类相似度是利用各簇中对象的均值来进行计算的。
k-means 算法的处理流程如下。首先,随机地选择 k 个数据对象,每个数据对象代表一个簇中心,即选择 k 个初始中心;对剩余的每个对象,根据其与各簇中心的相似度(距离),将它赋给与其最相似的簇中心对应的簇;然后重新计算每个簇中所有对象的平均值,作为新的簇中心。
不断重复以上这个过程,直到准则函数收敛,也就是簇中心不发生明显的变化。通常采用均方差作为准则函数,即最小化每个点到最近簇中心的距离的平方和。
新的簇中心计算方法是计算该簇中所有对象的平均值,也就是分别对所有对象的各个维度的值求平均值,从而得到簇的中心点。例如,一个簇包括以下 3 个数据对象 {(6,4,8),(8,2,2),(4,6,2)},则这个簇的中心点就是 ((6+8+4)/3,(4+2+6)/3,(8+2+2)/3)=(6,4,4)。
k-means 算法使用距离来描述两个数据对象之间的相似度。距离函数有明式距离、欧氏距离、马式距离和兰氏距离,最常用的是欧氏距离。
k-means 算法是当准则函数达到最优或者达到最大的迭代次数时即可终止。当采用欧氏距离时,准则函数一般为最小化数据对象到其簇中心的距离的平方和,即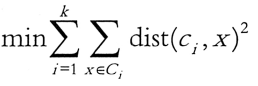 。
。
其中,k 是簇的个数,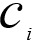 是第 i 个簇的中心点,dist(
是第 i 个簇的中心点,dist(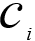 ,x)为 X 到
,x)为 X 到 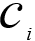 的距离。
的距离。
2. Spark MLlib 中的 k-means 算法
Spark MLlib 中的 k-means 算法的实现类 KMeans 具有以下参数。
class KMeans private (
private var k: int,
private var maxiterations: Int,
private var runs: Int,
private var initializationMode String
private var initializationStep: Int,
private var epsilon: Double,
private var seed: Long) extends: Serializable with Logging
1)MLlib 的 k-means 构造函数
使用默认值构造 MLlib 的 k-means 实例的接口如下。
{k: 2,maxIterations: 20,runs: 1, initializationMode: KMeans.K_MEANS_PARALLEL,InitializationSteps: 5,epsilon: le-4,seed:random}。
参数的含义解释如下。
| 名称 | 说明 |
|---|---|
| k | 表示期望的聚类的个数。 |
| maxIterations | 表示方法单次运行的最大迭代次数。 |
| runs | 表示算法被运行的次数。k-means 算法不保证能返回全局最优的聚类结果,所以在目标数据集上多次跑 k-means 算法,有助于返回最佳聚类结果。 |
| initializationMode | 表示初始聚类中心点的选择方式,目前支持随机选择或者 K_MEANS_PARALLEL 方式,默认是 K_MEANS_PARALLEL。 |
| initializationsteps | 表示 K_MEANS_PARALLEL 方法中的步数。 |
| epsilon | 表示 k-means 算法迭代收敛的阈值。 |
| seed | 表示集群初始化时的随机种子。 |
通常应用时,都会先调用 KMeans.train 方法对数据集进行聚类训练,这个方法会返回 KMeansModel 类实例,然后可以使用 KMeansModel.predict 方法对新的数据对象进行所属聚类的预测。
2)MLlib 中的 k-means 训练函数
MLlib 中的 k-means 训练函数 KMeans.train 方法有很多重载方法,这里以参数最全的一个 来进行说明。KMeans.train 方法如下。
def train(
data:RDD[Vector],
k:Int
maxIterations:Int
runs:Int
initializationMode: String,
seed: Long): KMeansModel = {
new KMeans().setK(k) -
.setMaxIterations(maxIterations)
.setRuns(runs)
.setInitializatinMode(initializationMode)
.setSeed(seed)
.run(data)
}
)
方法中各个参数的含义与构造函数相同,这里不再重复。
3)MLlib 中的 k-means 的预测函数
MLlib 中的 k-means 的预测函数 KMeansModel.predict 方法接收不同格式的数据输入参数,可以是向量或者 RDD,返回的是输入参数所属的聚类的索引号。KMeansModel.predict 方法的 API 如下。
def predict(point:Vector):Int
def predict(points:RDD[Vector]):RDD[int]
第一种预测方法只能接收一个点,并返回其所在的簇的索引值;第二个预测方法可以接收一组点,并把每个点所在簇的值以 RDD 方式返回。
3. MLlib 中的 k-means 算法实例
实例:导入训练数据集,使用 k-means 算法将数据聚类到两个簇当中,所需的簇个数会作为参数传递到算法中,然后计算簇内均方差总和(WSSSE),可以通过增加簇的个数 k 来减小误差。
本实例使用 k-means 算法进行聚类的步骤如下。
① 装载数据,数据以文本文件的方式进行存放。
② 将数据集聚类,设置类的个数为 2 和迭代次数为 20,进行模型训练形成数据模型。
③ 打印数据模型的中心点。
④ 使用误差平方之和来评估数据模型。
⑤ 使用模型测试单点数据。
⑥ 进行交叉评估 1 时,返回结果;进行交叉评估 2 时,返回数据集和结果。
该实例使用的数据存放在 kmeansdata.txt 文档中,提供了 6 个点的空间位置坐标,数据如下所示。
0.0 0.0 0.0
0.1 0.1 0.1
0.2 0.2 0.2
9.0 9.0 9.0
9.1 9.1 9.1
9.2 9.2 9.2
每行数据描述了一个点,每个点有 3 个数字描述了其在三维空间的坐标值。将数据的每一列视为一个特征指标,对数据集进行聚类分析。实现的代码如下所示。
import org.apache.log4j.{Level,Logger}import org.apache.spark.{SparkConf,SparkContext}import org.apache.spark.mllib.clustering.KMeansimport org.apache.spark.mllib.linalg.Vectorsobject Kmeans { def main(args: Array[String]) { //设置运行环境 val conf = new SparkConf().setAppName(“Kmeans”).setMaster(“local[4]”) val sc = new SparkContext(conf) //装载数据集 val data = sc.textFile(“/home/hadoop/exercise/kmeans_data.txt”, 1) val parsedData = data.map(s => Vectors.dense(s.split(‘’).map(.toDouble))) //将数据集聚类,设置类的个数为2,迭代次数为 20,进行模型训练形成数据模型 val numClusters = 2 val numIterations = 20 val model = KMeans.train(parsedData,numClusters, numIterations) //打印数据模型的中心点 printIn(“Cluster centers:”) for (c <- model.clustercenters) { printIn (“” + c.toString) } //使用误差平方之和来评估数据模型 val cost = model.computeCost(parsedData) printIn(“Within Set Sum of Squared Errors = “ + cost) //使用模型测试单点数据 printIn(“Vectors 0.2 0.2 0.2 is belongs to clusters:” + model.predict(Vectors.dense(“0.2 0.2 0.2”.split(‘’).map(.toDouble)))) printIn(“Vectors 0.25 0.25 0.25 is belongs to clusters:” + model.predict(Vectors.dense(“0.25 0.25 0.25”.split(‘’)).map(.toDouble)))) printIn(“Vectors 8 8 8 is belongs to clusters:” +model.predict(Vectors.dense(“8 8 8”.split(‘ ‘).map(.toDouble)))) //交叉评估 1,只返回结果 val testdata = data.map(s => Vectors.dense(s.split(‘’).map(.toDouble))) val result1 = model.predict(testdata) result1.saveAsTextFile (“/home/hadoop/upload/class8/resultkmeans1”) //交叉评估 2,返回数据集和结果 val result2 = data.map { line => val linevectore = Vectors.dense(line.split(‘’).map(.toDouble)) val prediction = model.predict(linevectore) line + “ “ + prediction }.saveAsTextFile(“/home/hadoop/upload/class8/result_kmeans2”) sc.stop () }}
运行代码后,在运行窗口中可以看到计算出的数据模型,以及找出的两个簇中心点:(9.1, 9.1, 9.1) 和 (0.1, 0.1, 0.1);并使用模型对测试点进行分类,可求出它们分别属于簇 1、1、0。
同时,在 /home/hadoop/spark/mllib/exercise 目录中有两个输出目录:result_kmeansl 和 result_kmeans2。在交叉评估 1 中只输出了 6 个点分别属于簇 0、0、0、1、1、1;在交叉评估 2 中输出了数据集和每个点所属的簇。
4. 算法优缺点
k-means 聚类算法是一种经典算法,该算法简单高效,易于理解和实现;算法的时间复杂度低,为O(tkm),其中,r 为迭代次数,k 为簇的数目,m 为记录数,n 为维数,并且 t<<m k<<n。
k-means 算法也有许多不足的地方。
- 需要人为事先确定簇的个数,k 的选择往往会是一个比较困难的问题。
- 对初始值的设置很敏感,算法的结果与初始值的选择有关。
- 对噪声和异常数据非常敏感。如果某个异常值具有很大的数值,则会严重影响数据分布。
- 不能解决非凸形状的数据分布聚类问题。
- 主要用于发现圆形或者球形簇,不能识别非球形的簇。

