完全二叉树：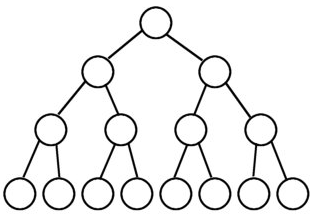
    堆排序 - 图1
    满二叉树（完全二叉树的一种）
    堆排序 - 图2
    比较典型的完全二叉树（叶子节点必须从左往右排列）

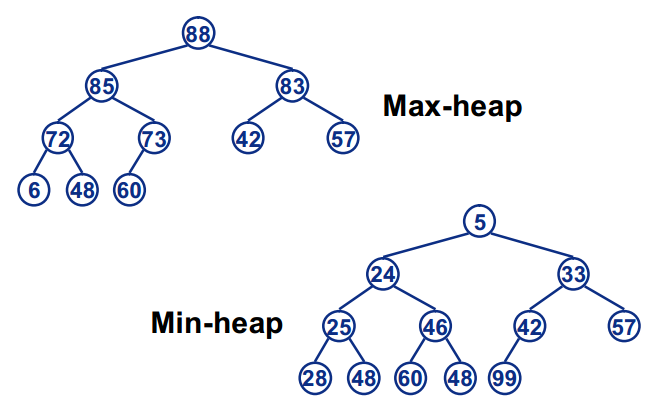
    堆排序 - 图3
    大根堆（堆就是完全二叉树）
    所有子树的根节点大于它下面所有的节点
    小根堆
    所有子树的根节点都小于它的所有的节点

    完全二叉树可以用数组表示，arr[]
    假如当前节点在数组中以arr【i】代表，则它的左子节点为arr【2i + 1】，右子节点为arr【2i + 2】
    求当前节点父节点（i）在数组中的索引 ：( i - 1 ) / 2。

    建立大根堆
    image.png

    当堆的节点发生变化时，堆的调整过程（heapify）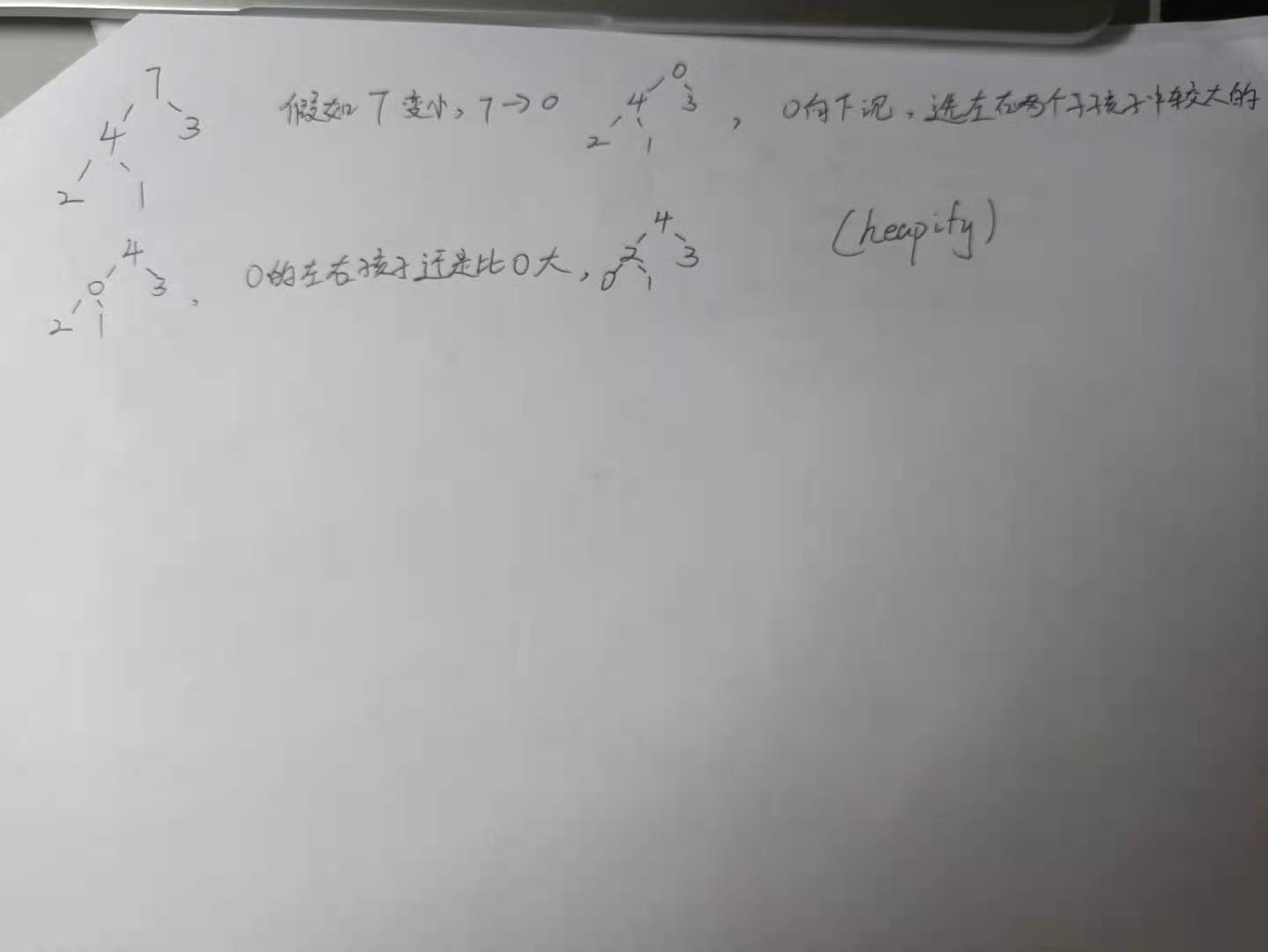
    image.png

    堆排序
    image.png

    应用：
    有海量数据，不断吐出数字，每吐出一个数字，要计算出已经吐出的数字的中位数。
    使用一个数组记录，有新数字进入再使用快速排序排列的话，每吐出一个数字，就要付出O（Nlog（N））的代价排序。
    当使用大根堆小根堆进行接收，每次吐出数字，堆进行调整的代价仅为O（logN），大根堆装较小的数，小根堆装较大的数。当吐出的数大于小根堆的根节点，就去小根堆。吐出的数字小于大根堆的根节点，去大根堆。当两个堆的heapsize差值大于1，从较大的那个堆吐出根节点到另一个堆。