算法复杂度

时间复杂度

概念

指输入数据大小为N时，算法运行所需要的时间。
注意：

• 统计的是算法的【计算操作数量】，而不是【运行的绝对时间】；计算操作数量和运行绝对时间呈正相关关系，并不相等。算法运行时间受到（编程语言、计算机处理器速度、运行环境）等多种因素影响。
• 体现的是计算操作随数据N变化时的变化情况。

• 假设算法运行时总共需要1次操作、100次操作，此两种情况的时间复杂度都为常数级O(1)；需要N次操作、100N次操作的时间复杂度都为O(N)

  符号表示

• 最差 —— O

• 平均 —— Θ
• 最佳 —— Ω

示例：

boolean findSeven(int[] nums){
    for (int num : nums){
        if (num == 7){
            return true;
        }
    }
    return false;
}

• 最佳情况Ω(1)：nums[7,a,s,d,f…]，即当数组首个数字为7时，无论nums有多少元素，循环次数都为1。
• 最差情况O(N)：nums[a,s,c,f,f…]且nums中所有数字都不为7时，此时会遍历整个数组，循环N次。
• 平均情况Θ：需要考虑输入数据的分布情况，计算所有数据情况下的平均时间复杂度。
  • 本题目需要考虑数组长度、数组元素的取值范围等。

注意：
O是最常用的时间复杂度评价渐进符号。

常见种类

从小到大：
O(1) < O(logN) < O(N) < O(N log N) < O(N2) < O(2N) < O(N!)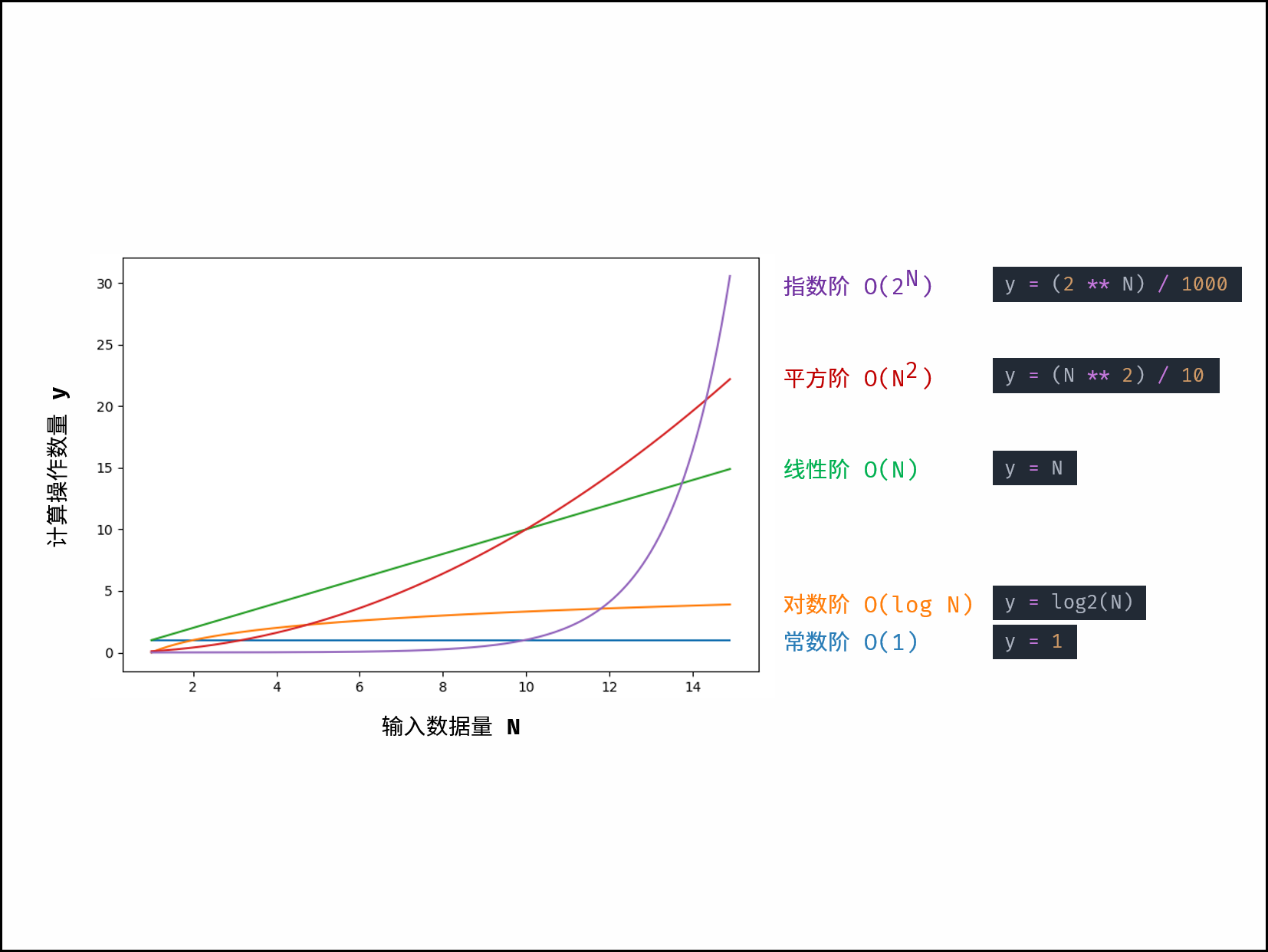

示例解析

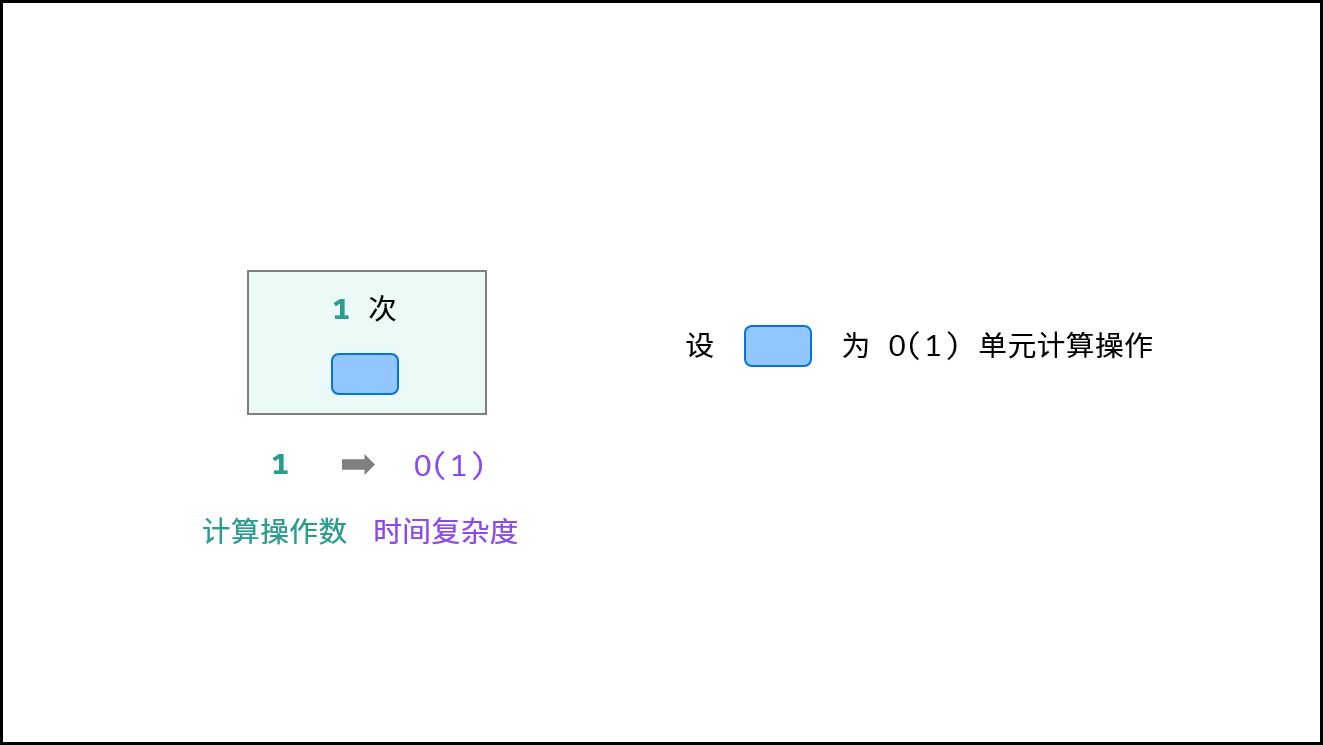
常数O(1)

运行次数与N大小呈常数关系，即不随输入数据大小N的变化而变化。

int algorithm(int N) {
    int a = 1;
    int b = 2;
    int x = a * b + N;
    return 1;
}
int algorithm(int N) {
    int count = 0;
    int a = 10000;
    for (int i = 0; i < a; i++) {
        count++;
    }
    return count;
}

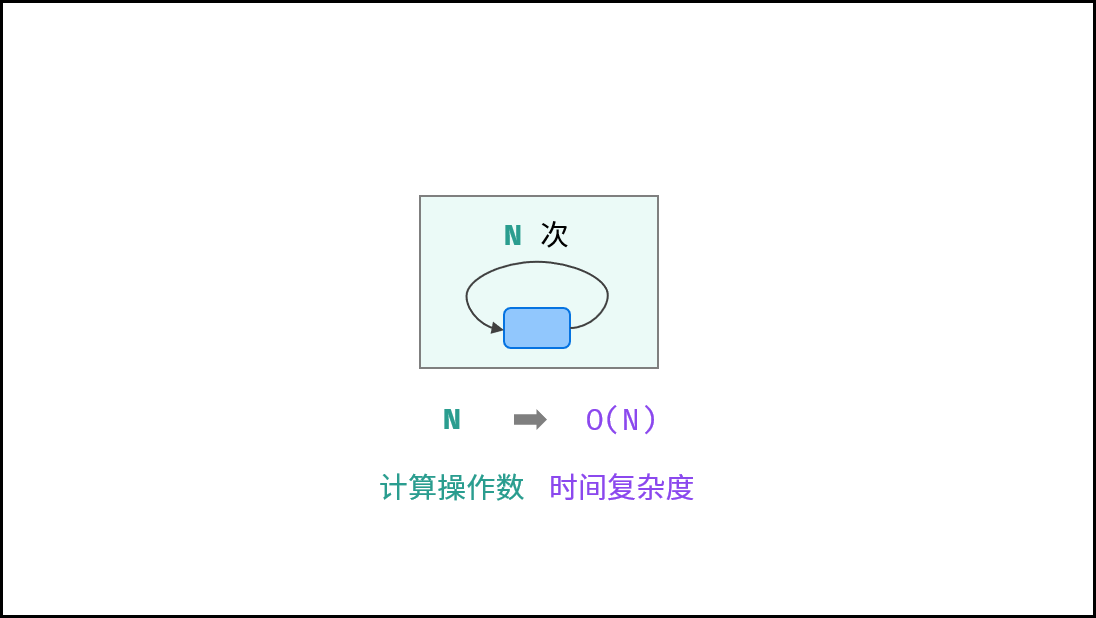
线型O(N)

循环运行次数与N大小呈线型关系，时间复杂度为O(N)
示例：

int algorithm(int N){
    int count = 0;
  for (int i = 0; i < N; i++){
      count++;
  }
  return count;
}
//以下代码虽然是两层循环，但是第二层与N的大小无关，因此整体仍与N呈线型关系
int algorithm(int N){
    int count = 0;
  int a = 10000;
  for (int i = 0; i < N; i++){
      for (int j = 0; j < a; j++){
        count++;
    }
  }
  return count;
}

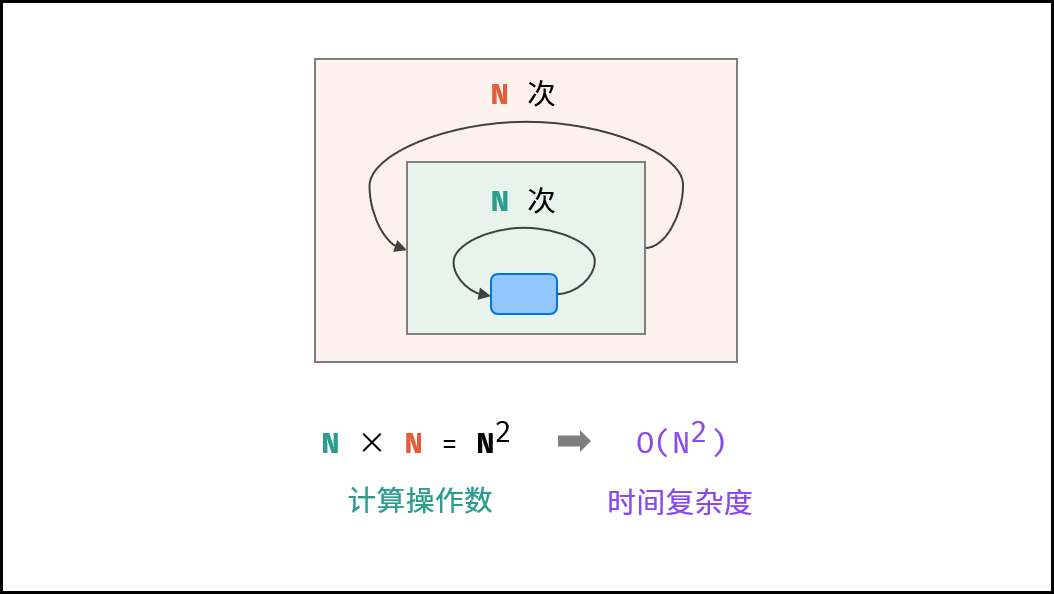
平方O(N2)

两层循环相互独立，都与N呈线型关系，因此总体与N呈平方关系，时间复杂度为O(N2)。
示例：

int algorithm(int N){
    int count = 0;
    for (int i = 0; i < N; i++){
        for (int j = 0; j < N; j++){
            count++;
        }
    }
    return count;
}

以【冒泡排序】为例，其包含两层独立循环：

1. 第一次复杂度为O(N)
2. 第二层平均循环次数为N/2，复杂度为O(N)
3. 推导过程如下：
   1. O(N/2) = O(1/2)O(N) = O(1)O(N) = O(N)

因此，冒泡排序的总体时间复杂度为O(N2)，代码示例：

int[] bubbleSort(int[] nums){
    int N = nums.length;
    for (int i = 0; i < N-1; i++){
        for (int j = 0; j < N-1-i; j++){
            if (nums[j] > nums[j+1]){
                int tmp = nums[j];
                nums[j] = nums[j+1];
                num[j+1] = tmp;
            }
        }
    }
    return nums;
}

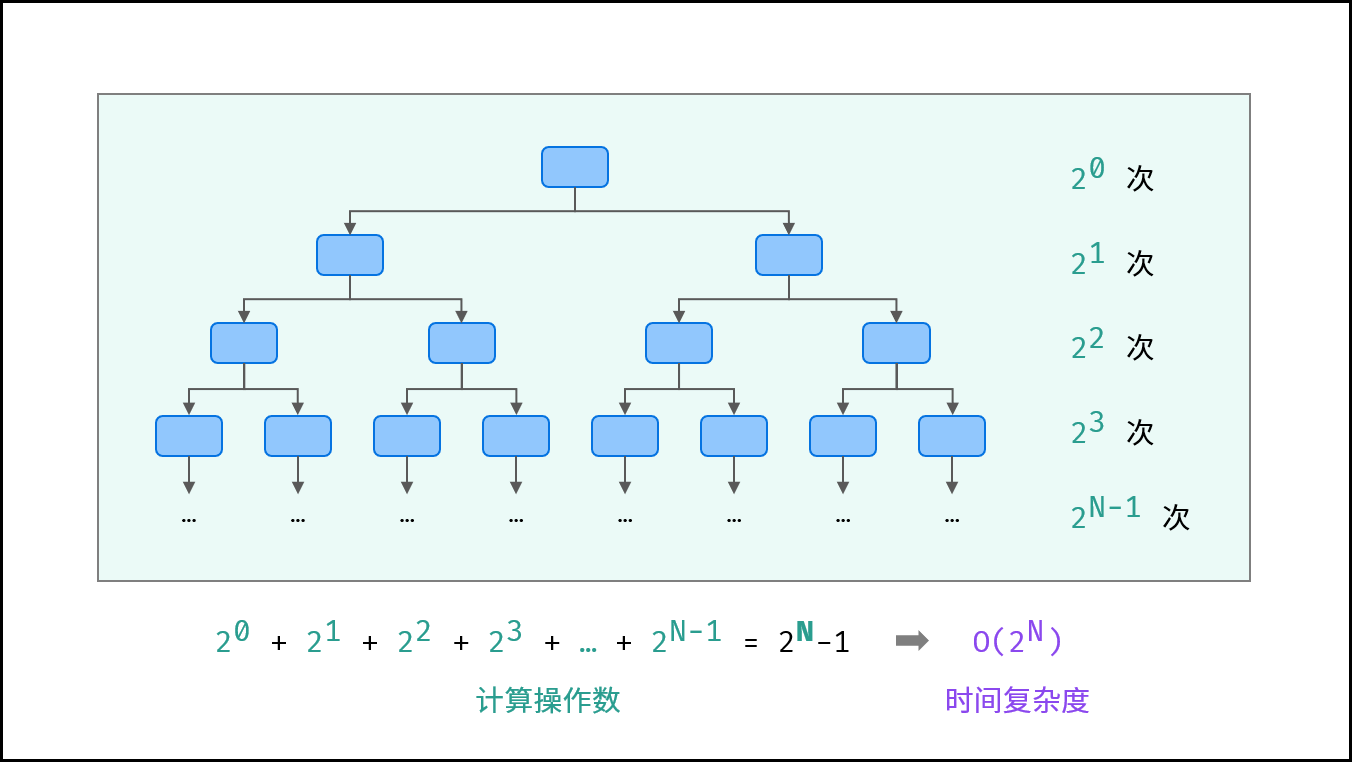
指数O(2N)

生物学科中的“细胞分裂”即是指数级增长。初始状态为1个细胞，分裂一轮后为2个，分裂两轮后为4个，……，分裂N轮后有2N个细胞。
代码示例：

int algorithm(int N){
    if (N <= 0){
        return 1;
    }
    int count_1 = algorithm(N-1);
    int count_2 = algorithm(N-1);
    return count_1 + count_2;
}

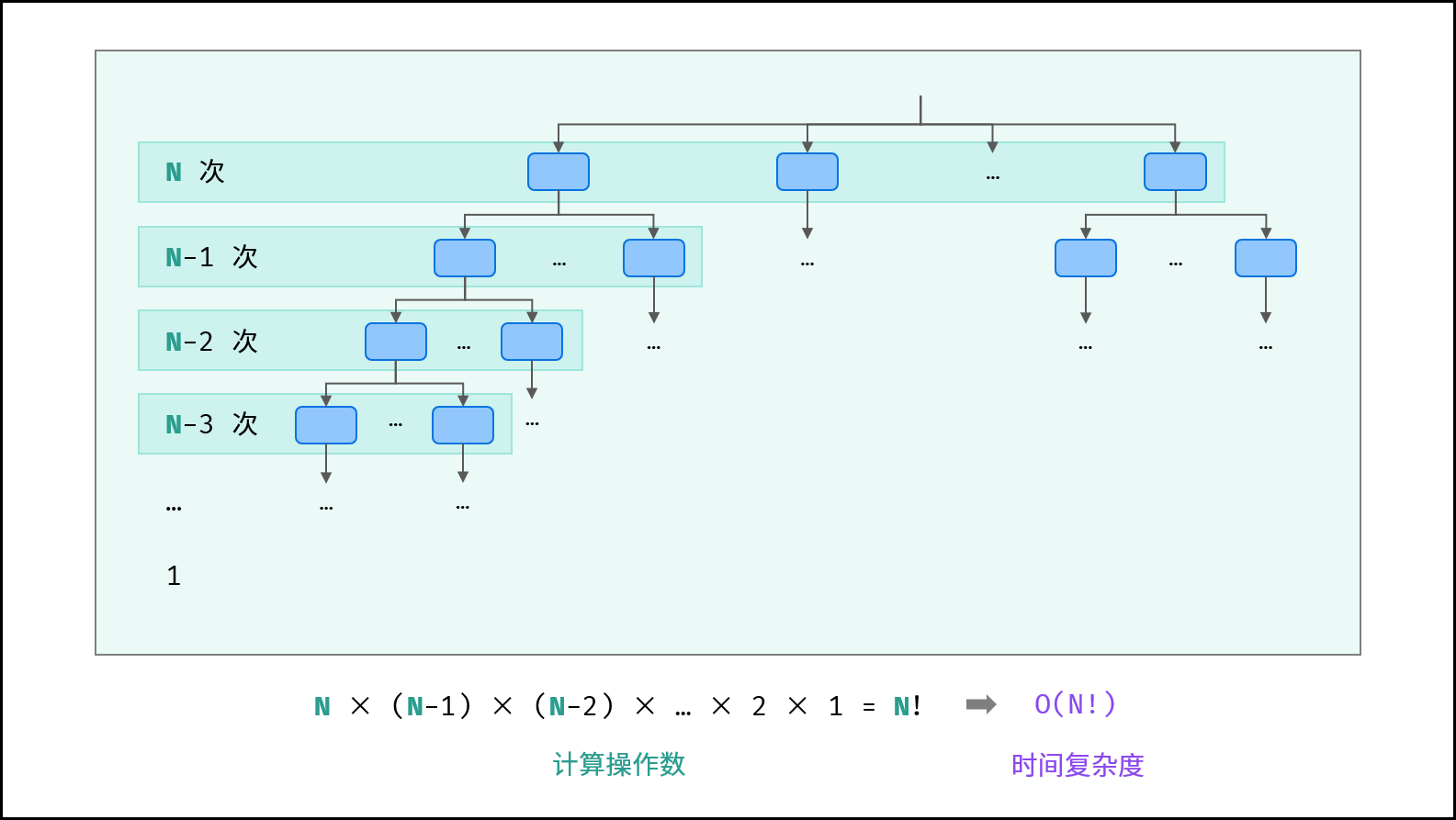
阶乘O(N!)

阶乘阶对应数学上常见的“全排列”。即给定N个互不重复的元素，求其所有可能的排列方案：
N (N - 1) (N - 2) …… 2 * 1 = N!
阶乘通常使用递归实现，算法原理：
第一层分裂出N个，第二层分裂出N-1个，……直到第N层终止并回溯；

int algorithm(int N) {
    if (N <= 0) {
        return 1;
    }
    int count = 0;
    for (int i = 0; i < N; i++) {
        count += algorithm(N - 1);
    }
    return count;
}

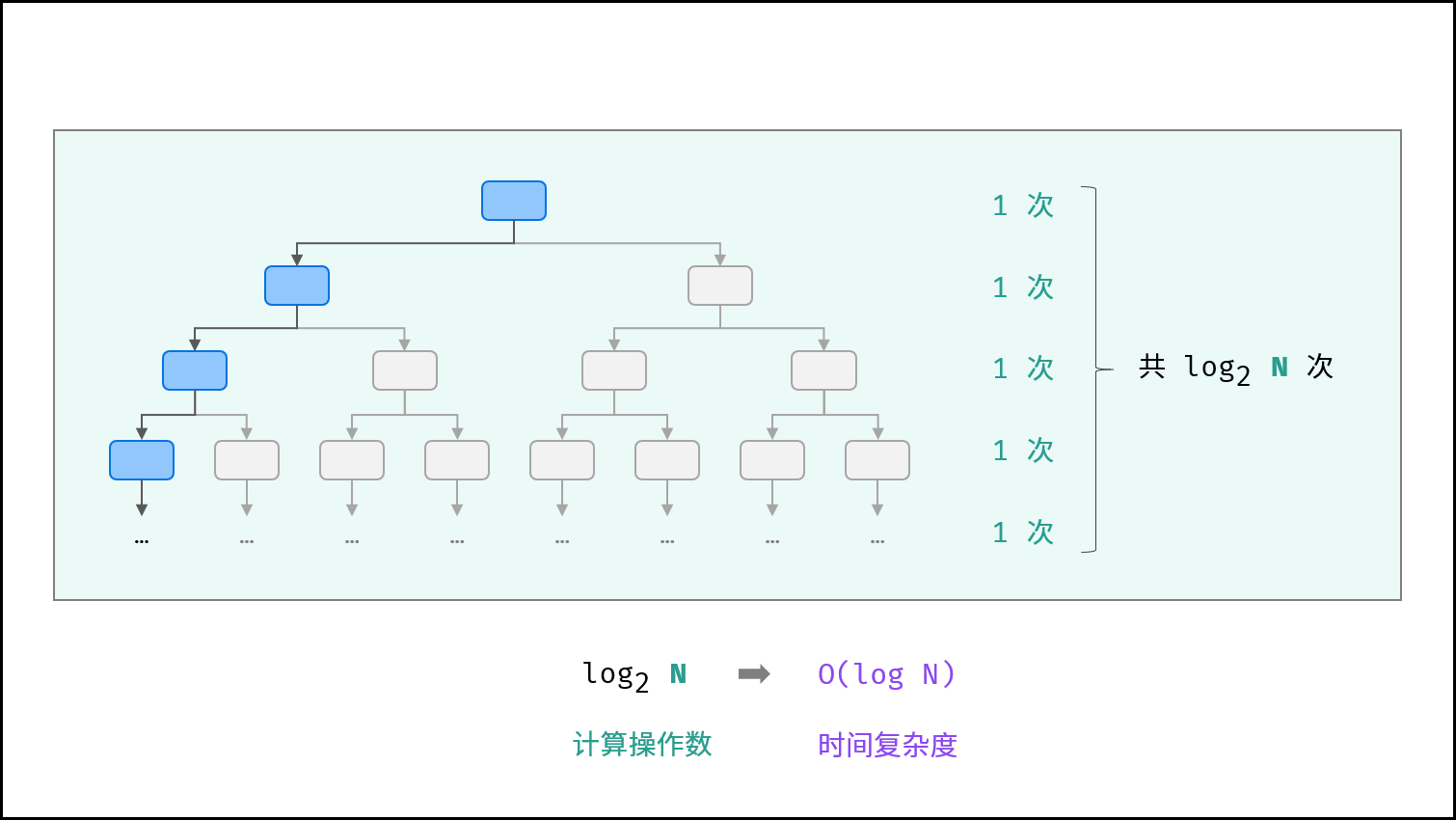
对数O(log N)

对数阶与指数阶相反，指数阶为“每轮分裂出两倍的情况”，而对数阶是“每轮排除一半的情况”。
对数阶常出现于【二分法】、【分治】算法，体现着：一分为二和一分为多的算法思想。
示例：
设置循环次数为m，则输入数据大小N与2m呈线型关系，两边同时取log2对数，则得到循环次数m与log2N呈线性关系，即时间复杂度为O(logN)

int algorithm(int N){
    int count = 0;
    folat = N;
    while (i > 1){
        i = i / 2;
        count ++;
    }
    return count;
}

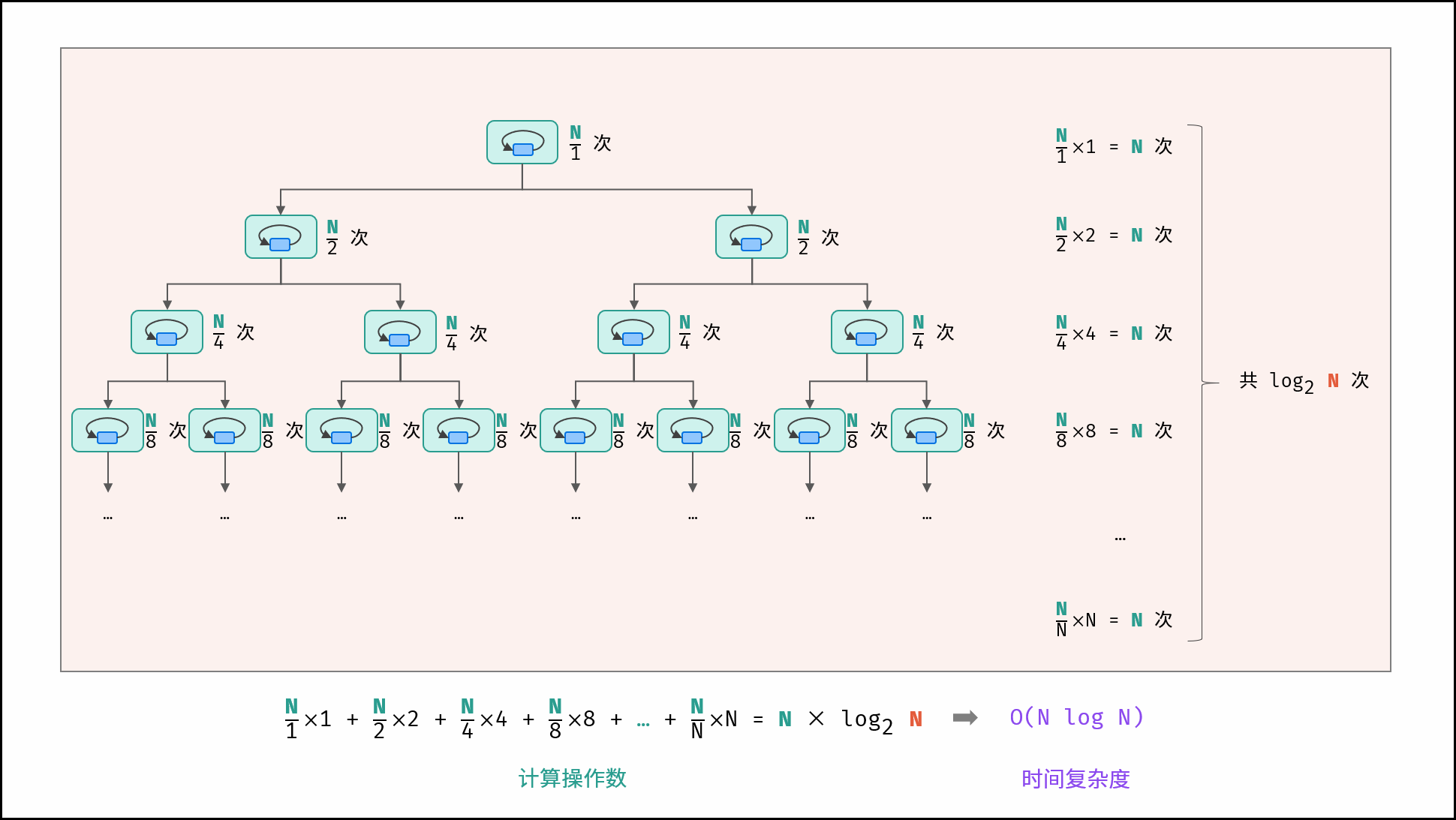
线性对数O(N log N)

概念：
两层循环相互独立，第一层和第二层时间复杂度分别为O(log N)和O(N)，则总体时间复杂度为O(N log N)。

int algorithm(int N) {
    int count = 0;
    float i = N;
    while (i > 1){
        i = i / 2;
        for (int j = 0; j < N; j++){
            count ++;
        }
    }
    return count;
}

线型对数阶常出现于排序算法，例：快速排序、归并排序、堆排序等。
时间复杂度原理图：

示例题目

空间复杂度