前言

immer.js采用了持久化数据结构和结构共享，保证每一个对象都是不可变的，任何添加、修改、删除等操作都会生成一个新的对象，且通过结构共享等方式大幅提高性能。其参考了 Clojure 中的Persistent Vector的实现，本篇文章就是对clojure的Persistent Vector的实现原来做介绍。

文章翻译自：Understanding Clojure’s Persistent Vectors, pt. 1，参考自：understanding，略有修改。

你可能听过clojure的persistent vector，也可能没有听说过。Rich为clojure开发了这个数据结构（灵感来自Phil Bagwell的论文Ideal Hash Tree），使得append、update、lookup和subvec的时间复杂度为O(1)。因为所有的vector都是持久化的，所有对vector的修改操作都不会改变原来结构，而是生成一个全新的vector。

听起来非常不可思议，但这怎么能做到呢？我会在本文详细介绍它的实现，以及实现过程中的一些技巧。

首先，我们看一下3个基础操作：update、append、popping。这3个操作是Clojure Persistent Vector的内核，稍后，我们再看看一些对常用便捷操作上的优化，比如transient和tail。

基本思路

C++ STL的vector和Java的ArrayList底层使用最基础的数组实现，在空间不够的时候，会自动分配内存。如果你想要可变性，这就是完美的，但如果你想要持久性，这就行不通。要实现持久性，你就需要频繁的生成新对象，这会导致修改操作变得极慢，且内存消耗速增。怎么才能在查询和修改时避免这种底层数据的拷贝以获得最佳性能？这就是clojure 的persistent vector实现所完成的工作，它的实现实际上是一颗平衡排序树。

我们先看这样一颗类二叉树。和普通二叉树不同是，树的内部结点最多两个子节点，且不含任何值。叶结点也最多包含两个值。所有值都是排好序的，也就是，最左边的叶节点包含序列里最小的值，最右边的叶节点包含序列里最大的值。我们暂时假设所有叶节点的深度相同（可以认为这是路径选择的一种简化，虽然JVM会对路径选择优化起到一些作用，但这个后文再详细讨论）。请看下面这棵树，包含了0~8 9个整数，0是第一个元素，8是最后一个元素，9是这个vector的大小。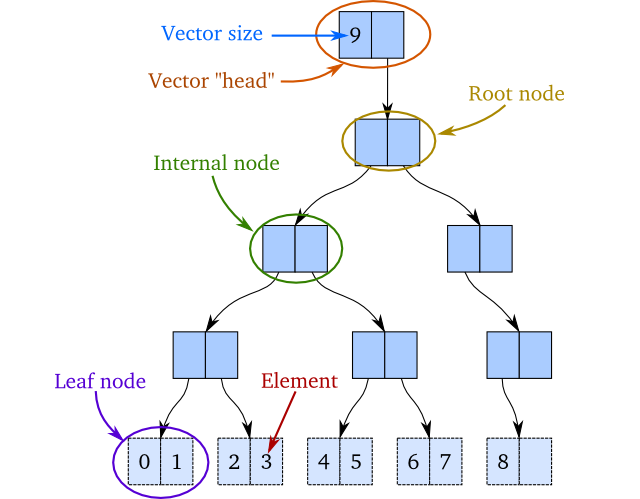
图片.png

如果要在vector尾部插入一个新的元素，在一个可变性主宰的世界里，结果会是这样，把9插入到最右边的叶子节点：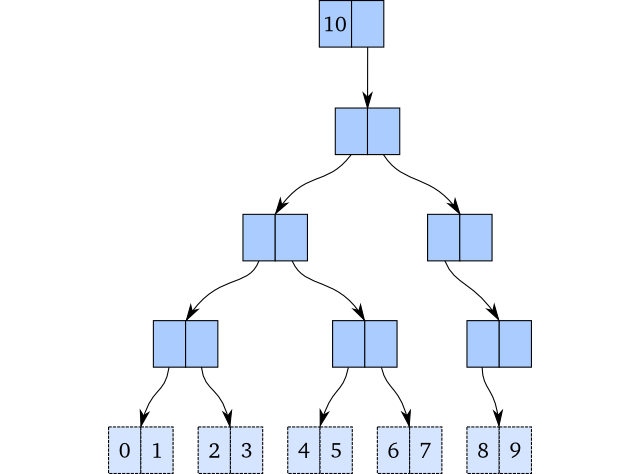
图片.png

但问题是：这改变了原来的数据结构！如果想要基于这种实现获得持久性的修改操作，就需要拷贝整颗树（或者至少树的一部分）。
既要保留持久性，又要最小化底层的拷贝操作，我们想到一种方法：路径拷贝，只拷贝从根节点到需要修改（update，insert，replace）的叶节点的整条路径。多次插入的操作演示如下，有7个元素的vector与有10个元素的vector共享了部分数据结构：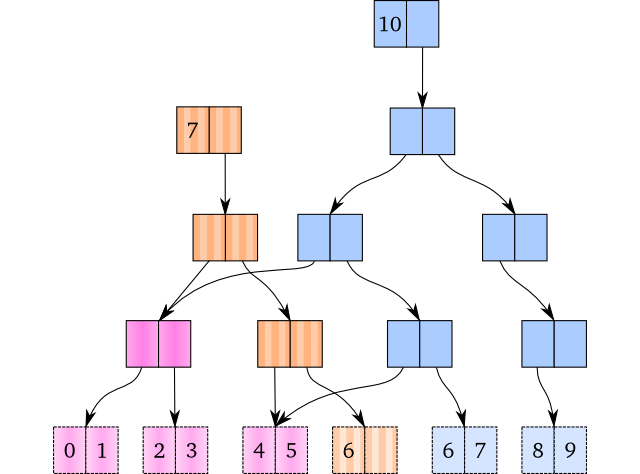
图片.png

粉色的节点由两个vector共享，棕色和蓝色的分别属于各vector自己，如果还有其他操作，新生成的vector可能会和这两个vector有更多的节点共享。

更新

最简单的修改操作就是更新/替换值，在clojure中，由assoc或者update-in/update实现。
更新一个元素，先沿着树遍历到需要更新的节点，遍历过程就会拷贝遍历过的路径以保证后续的持久性，遍历到节点后，直接拷贝出一个新的节点，然后把值替换掉，然后返回一个新的vector，这个新的vector包含的是拷贝出来的新的路径。
举个栗子。在vector上执行一个assoc操作：

  1. (def brown [0 1 2 3 4 5 6 7 8])
  2. (def blue (assoc brown 5 'beef))

操作演示如下，蓝色vector是拷贝出来的新路径：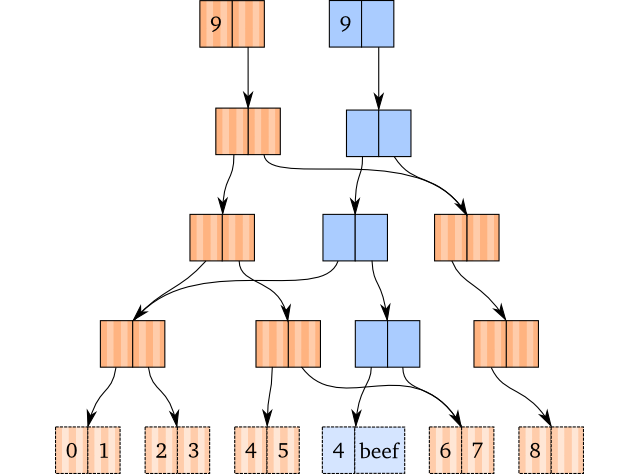
图片.png

假设我们已经知道如何获取需要遍历的路径（后文会介绍这个部分），这个操作还算简单。

追加

追加(Append，即尾部插入)和更新大体相同，但是有一些边界问题需要处理，可能会要求生成新的叶节点，基本上，分下面3中情况：

  1. 最右边的叶节点还有空间
  2. 根节点有空间，但最右叶节点没有空间
  3. 根节点没有空间

下面逐个看一下。

1: 和Assoc操作一致

只要最右叶节点还有空间，其实和assoc更新操作完全一致：拷贝路径，创建新节点，把新的元素放入新节点内。举个栗子：下面的图演示了操作(conj [0 1 2 3 4] 5)，蓝色是新生成的节点，棕色是原数据结构：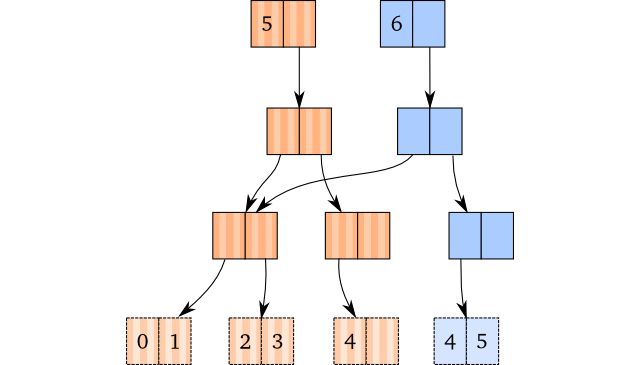
图片.png
就这样。这里没有什么黑魔法，只有路径的复制以及叶子节点的插入。

2: 按需生成新节点

如果最右叶节点没有空间呢？没关系，只要能找到正确的路径到达叶节点就ok了，幸运的是我们总能找到这样一条路径，毕竟它是一颗二叉树。但是…会发现这条路径其实还不存在…当一个节点不存在的时候，我们就生成新的节点，把这个新节点当成是拷贝来的节点，后续的操作就和前面一样了：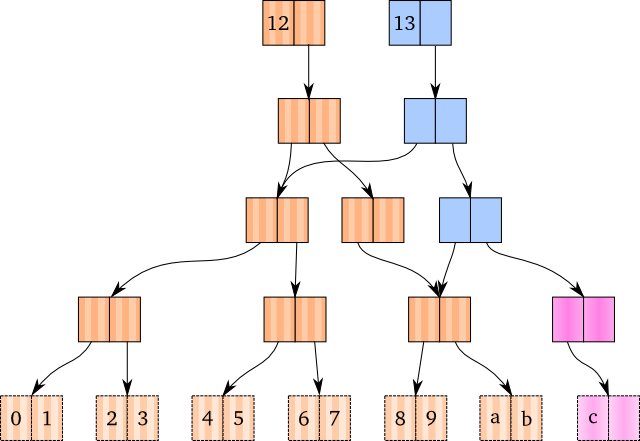
图片.png

上图，粉色节点是新生成的，蓝色是真正拷贝来的。

3: 根节点溢出

最后一种情况是根节点溢出，也就是根节点没有空间了（其实就是所有节点的子节点数都是2），不难理解，我们只能在根节点之上再加新节点，这样老根节点是原数据结构的根节点，是新数据结构根节点的子节点，新加的节点就是新数据结构的根节点，后续的操作也和前面一致了。看似有点绕，但如图所示，其实很简单：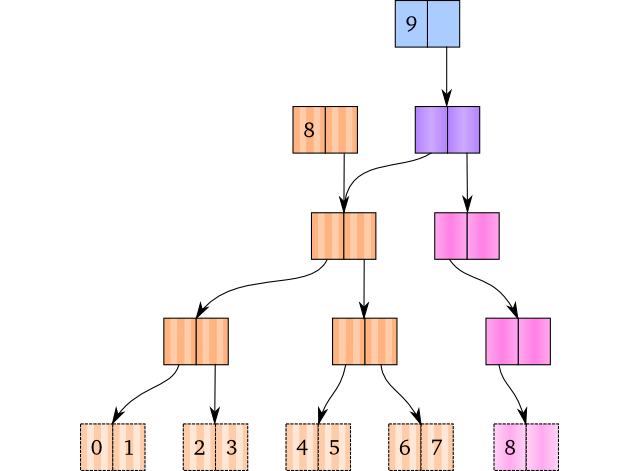
图片.png

解决这个case还是相对简单，但当你进行append操作的时候，如何鉴别根节点是否有足够空间呢？方法也很简单，因为我们是二叉树，所有当vector的大小正好是2的次幂的时候，原来的vector根节点就溢出了，更通用的是，当我们是一颗n叉树的时候，当vector的大小是n的次幂的时候根节点就溢出了。

弹出(Popping)

弹出操作(popping, 删除尾部元素)也比较简单，它和追加操作比较相似：

  1. 最右叶节点包含不止个元素
  2. 最右叶节点包含一个元素
  3. 执行popping操作后，根节点只有一个元素

本质上，这就是append操作3中情况的逆操作，都很简单。

1: dissoc to the rescue

只要最右叶节点在执行popping操作后还有至少一个元素，我们就直接拷贝路径和节点，完成操作：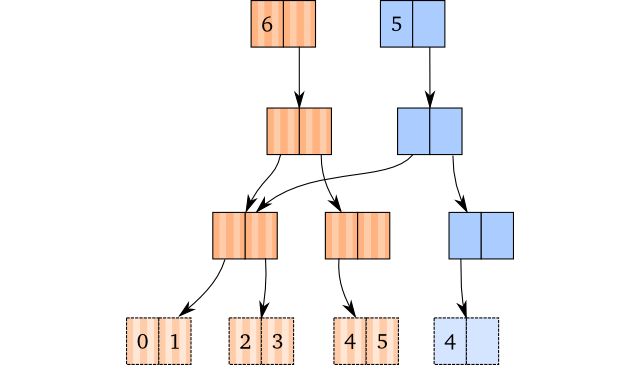
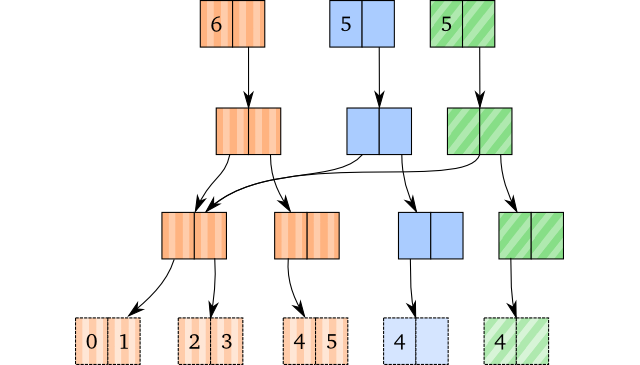
图片.png

记住，在一个vector上多次执行popping操作不会生成相同的vector，他们包含的元素相同，但他们不共享跟节点，举例：

  1. (def brown [0 1 2 3 4 5])
  2. (def blue (pop brown))
  3. (def green (pop brown))

就会有下面的内部结构：

图片.png

2: 删除空节点

如果执行完popping操作后，最右叶节点为空，那这个节点需要被回收，父节点不再指向这个节点，应该置空（空指针）。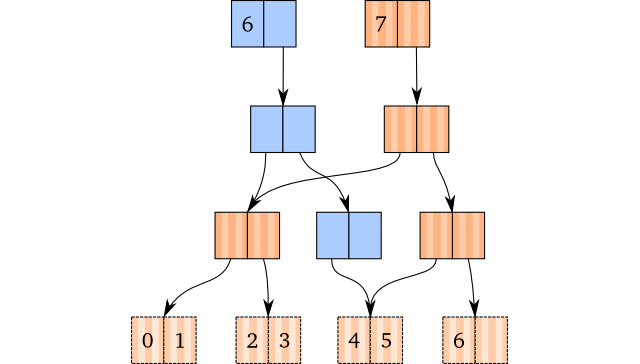
图片.png

注意，这次棕色的是pop前的vector，蓝色是pop后新生成的vector。
看起来仍然很简单，但其实有一个问题，假如，把空指针返回给一个节点，而这个节点原本就只有一个节点，也就是这个空指针节点，就必须把这个（父）节点也变成空指针，继续向上返回。所以，把一个节点置空的操作结果需要向上传递，实现起来可能会比较tricky，需要检查这个子节点是否为空，且子节点在父节点中的索引为0，如果是就继续向上返回空。

clojure的递归实现如下：

  1. (defn node-pop [idx depth cur-node]
  2.   (let [sub-idx (calculate-subindex idx depth)]
  3.     (if (leaf-node? depth)
  4.       (if (== sub-idx 0)
  5.         nil
  6.         (copy-and-remove cur-node sub-idx))
  8.       (let [child (node-pop idx (- depth 1)
  9.                             (child-at cur-node sub-idx))]
  10.         (if (nil? child)
  11.           (if (== sub-idx 0)
  12.             nil
  13.             (copy-and-remove cur-node sub-idx))
  14.           (copy-and-replace cur-node sub-idx child))))))

以上实现就可以保证移除空节点不会带来问题，下面的例子演示了新生成的蓝色的vector实际上删除了两个节点：叶子节点c和它的父节点：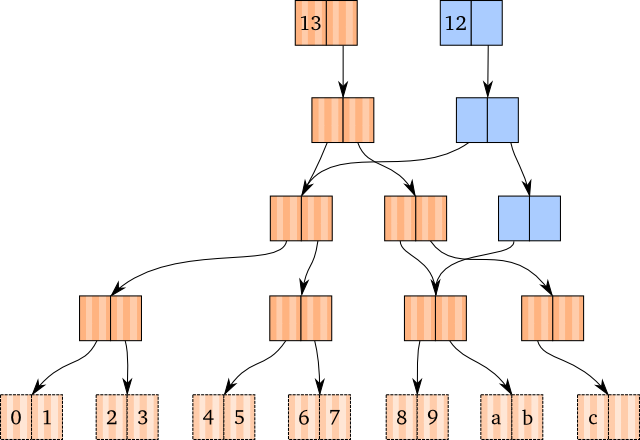
图片.png

3: Root Killing

还剩最后一种情况，依照上面的方法，以下棕色的树在移除8这个节点后会得到蓝色的树，如图：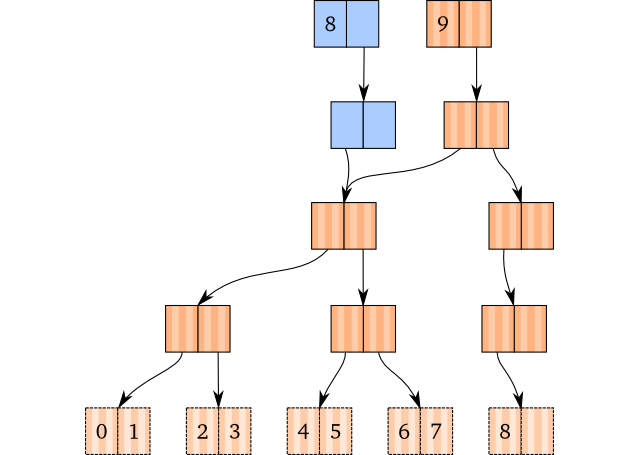
图片.png

没错，就是根节点只有一个子节点。这种树没有任何意义，因为查找的时候一定会直接找到它的子节点。所以需要把多余的根节点去掉。
这可能是目前为止最简单的操作了，popping完成，检查根节点是否只有一个子节点（检查第2个节点是否为空），如果只有一个子节点，且根节点不是叶子节点，我们就直接用它的子节点替换这个跟节点，相当于两个节点做了合并。结果如下，根节点下降了一层：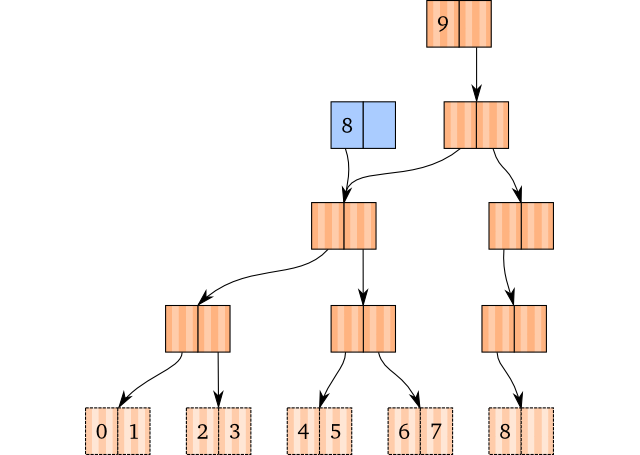
图片.png

O(1) != O(log n)

看到这里可能有人会问，这哪是O(1)时间复杂度？事实上，如果每个节点只有连个子节点，时间复杂度是O(log2 n)，远大于O(1)。
技巧就是，前面没有规定我们只能有2个子节点，只是为了解释方便选择了2个子节点作为假设，事实上，clojure的实现有32个子节点，这样，树的深度就会非常小，可以算一下，一个vector中有不到10亿个元素时，树的深度最多6层，需要350亿个元素才能把树的深度增加到8层。在这种情况下，内存消耗可能是一个更亟待考虑的严重问题。
举个实例，一个4叉树，包含14个元素，树的深度只有2，再看上面移除空节点的例子，2个vector各有13和12个元素，在2叉树的情况下，深度已经是4，等于下面这颗树的2倍。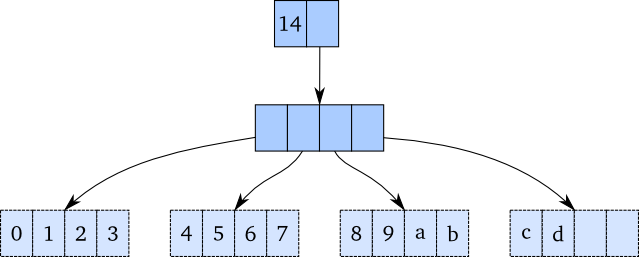
图片.png

在这种精心设计的层数极低的树结构下，我们倾向于认为所有的修改操作都接近于常数时间，虽然理论值等于O(log32 N)。对于理解时间复杂度的人会认为O(log32 N)和O(log N)是一样的，但为了便于市场推广，大家都喜欢说成是常数时间。

小节

以上主要描述了clojure的persistent vector内部如何实现，其update、append、popping操作的基本思路，以及如何在常数时间内完成这些操作，有关append和popping的加速优化会在文末介绍，接下来先讨论一些更重要的。