第二章 - 运算方法与运算器

一. 知识总结 :

1. 浮点数的运算

1.1 什么是规格化 ?

如上图 : 正常情况下存储的时候, 因为位数优先, 所以无法将尾数全部存储, 导致原本是 0.01001 , 现在只存储了 0.0100 , 导致了精度的缺失, 规格化就是规定了尾数的最高为必须是一个有效位, 换句话说就是不能是 0 ** **可以看到下面的进行规格化以后就变成了 0.10010 ,此时再进行存储的时候就不会出现精度损失

1.2 IEEE754 标准

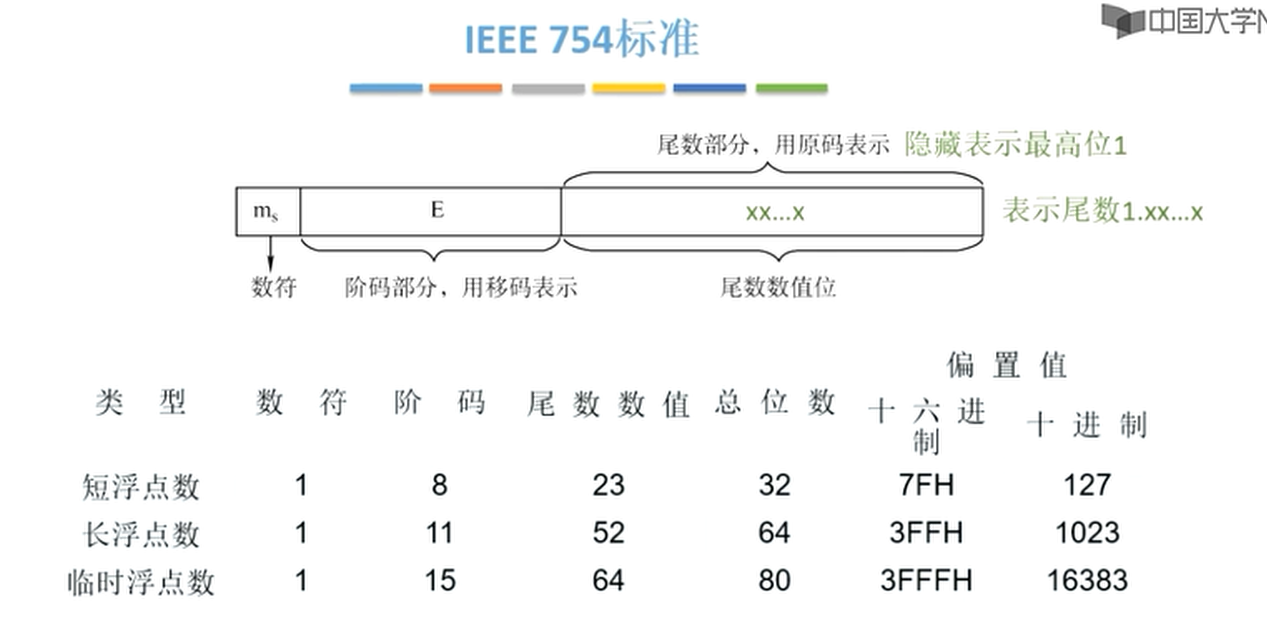
1.3 浮点数的运算步骤

例题 :
:::info 设阶码3位, 尾数6位, 按照浮点数的运算方法 完成下列取值的 [x + y] , [x - y ] 的运算 **

1. x = 2** 0.100101 y = 2** ( - 0.011110)**
2. x = 2** （ - 0.0.010110） y = 2** ( - 0.010110)**

:::

:::success 第一步 - 转换格式 : [X]补 = 两位符号位 , 阶码的补码 ; 两位符号位.尾数的补码
由于 y 不是规格化的数, 所以要对 y 进行规格化 : y的规格化形式为 y = 2**-011* (-0.11110)
y = 2**-010 * (-0.011110) => y = 2-011 (-0.111100)

阶码和尾数都是补码
[X]浮 = [X]补 = 11,101 ; 00.100101 **[Y]浮 = **[Y]补 = 11,101 ; 11.000100

第二步 - 对阶 : 对阶对的是 X浮和Y浮的值
对阶就是 保证阶码是一致的, 这样可以方便计算 比如 10**5** 5 + 102 6 => 105 5 + 105 0.006
补充 : **Ex 表示x的阶码, 也就是 11010 Ey = 11011 (正数的原码反码补码相同)
Ex补 = 11110 Ey补 = 11101 (-Ey)补 = (00011)补 = 00011
由 **Ex－Ey＝Ex补+ (－Ey)补＝11101+00011＝00000＝0 , 由于阶差为 0 所以不用二者阶码相同, 不需要对阶

最终 X浮 = 11101 ; 00.100101 Y浮 = 11101 ; 11.000100*

第三步 - 尾数加减运算

Mx + My = 00.100101 + 11.000100 = 11.101101
Mx + (-My) = 00.100101 + 00.111100 = 01.100001
Ex+y = 11101

第四步 - 规格化
(1) 左规 : 当尾数出现 00.xxx 或者 11.xxx 需要左规, 尾数左移, 小数点右移 , 阶码减 1
(2) 右规 : 当尾数出现 01.xxx 或者 10.xxx 需要右规, 尾数右移, 小数点左移 , 阶码加1**Mx + My 左规 尾数为 11.101101 => 11.011010 阶码 为 11101 =>11100
Mx - My 右规 尾数为 01.100001 => 00.110000 阶码 为 11101 =>11110**

第五步 - 舍入
在对阶和右规的过程中, 可能会将尾数低的位丢失 , 引起误差, 影响精度, 1234 1是低位, 4是高位
Mx + My 不需要舍入 => **11100 ; 11.011010
Mx + My 0舍1入 : 如果尾数右移的时候 移除的是 1,则在末尾加1 , 如果是 0 则舍去
11110; 00.110000=>** 11110;00.110001
注意 :舍入后的到的计算结果是 补码, 一定要记着转成原码 !
结果 :
x+y = 2**-100* (-0.100110)
x- y = 2**-110* 0.110001

第六步 - 溢出判断
如果符号

** :::

1.4 关于规格化移位的一些理解

:::tips 对于阶码和尾数是正数的规格化 :

比如 2** 0.01101 => 2** 0.11010 这个其实就相当于 10** 0.023 => 10** 0.23
尾数 0.023 -> 0.23 ,小数点向右移动,阶码减一**

对于阶码和尾数是负数的规格化 :
比如 2** (-0.01101) => 2** (-0.11010) 这个其实就相当于 10** -0.023 => 10** -0.23
尾数 -0.023 -> -0.23 , 小数点向右移动, 阶码减一

对于阶码和尾数有一个是负的规格化
比如 2** 0.01101 => 2** 0.11010 这个其实就相当于 10** 0.023 => 10** 0.23
比如 2** (- 0.01101) => 2** (-0.11010) 这个其实就相当于 10** (- 0.023) =>105**(-0.23)
其实 和 上面的没有任何区别 ,
总结 : 尾数小数点向右移动, 相当于这个尾数的绝对值变大了, 那么, 相对应的 阶码肯定要减小,
无论是阶码是正数还是负数, **

1. 小数点向右移动一位,阶码减1就行了 如果是负数 比如 -101 - 1 = -(101 + 1) = -110
2. 小数点向左移动一位,阶码加1就行了 ** -101 + 1 = -100**
   :::

1.5 如何对阶 ?

:::tips 举例 : x＝2**×(－0.010110)，y＝2**×0.010110
由于 x y 都没有进行规格化, 所以先进行规格化
x 规格化 => x＝2**×－0.101100 (阶码减一, 小数点向右移动, 尾数左移)
y 规格化 => y= 2**× 0.101100**

X浮和Y浮的阶码和尾数都是补码
X浮 = 11010 ; 11.010100 Y浮 = 11011 ; 00.101100

规格化以后 现在开始对阶 : 对阶对的是 X浮和Y浮的值
对阶的原则 : 小阶向大阶看齐, 因为小数点向右移动会引起最高位的丢失, 但是小数点向左移动, 会丢失最低位, 误差较小, 并且 双符号位的情况下, 最低位的符号位也会参与运算
阶码 : Ex = 11110 Ey = 11101 (-Ey)补 = (00101)补 = 00101 (Ex)补 = 11010

1. 计算阶差 : E = Ex - Ey = (Ex)补 + (-Ey)补 = 11010 + 00101 = (**11111**)补 => (11001)原 = -1
2. Ey > Ex , 所以 Ex 要向Ey 看齐, 阶码加 1 , 小数点向左移动1位 010 => 011 (双符号位最低为的符号位参与运算)
3. 11010;11.010100 => 11011;11.101010

对阶后的 x浮 = 11011;11.101010 y浮 = 11011;00.101100
** :::

2. 定点数的加减乘除

2.1 定点数的加法

:::tips 公式 :

[A+B] = [A]+ [B]
[A- B]补 = [A]补 - [B]补
** :::

:::info 设 机器字长为 8 位(含1位符号位) , A = 15, B=24 计算 A+B 和 A-B

A = +0001111 B = +0011000 A补 = 00001111 B补 = 00011000
(-B)补 = 11101000

A补 + B补 = 00100111 => 转为原码 01011001 =>

:::

二. 例题 :

题目一 : 计算32位浮点规格化数

:::info 将下列十进制数表示成IEEE754标准的32位浮点规格化数 :
(1) 27 / 64 (2) -27 / 64 :::

:::success

1. 第一步 : 27 / 64 = 27 2 => 11011 2
2. 第二步 : 移动小数点, 使其在 1,2 位之间 => 1.1011 * 2
3. 第三部 : 于是得到 S = 0 , E = 0 + 127 = 127, (127) = 1111111 M = 1011
4. 得到 32 位的2进制存储格式

0111 1111 1101 1000 0000 0000 0000 0000

:::

:::tips

1. S表示正负 0表示正, 1表示负, 通常是 1位
2. E表示阶码,在32位运算中 E = e + 127 , E通常是 8 位
3. M是尾数, 表示小数点后面的部分, 通常是 23位 , 不足的话在后面补零 :::