1 绘图基本概念

1.1 无向图和有向图

无向图：全部由无向边（没有箭头）构成的图称为无向图。
有向图：全部有有向边（有箭头）构成的图称为有向图。

1.2 出度和入度

出度和入度：以某一个点为基准，与之相关联的边中，以该点为起点的边的条数称为出度。反之，以该点为终点的边的条数称为入度。另外，一个边为自环边，起点和终点都为某个点自己，此时出度为一度，出度为一度，即一条自环边算两度。
度：一个点的入度和出度的总和成为该点的度。
如图：A点的出度是：3，入度为：2，总度数为5。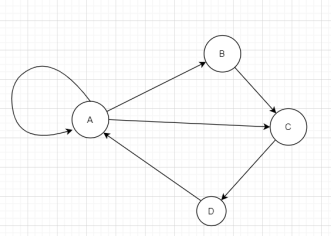

1.3 邻接矩阵

设无向图G=(V,E),其中顶点集V=v1,v2,…,vn，边集 E=e1,e2,…,em。
该图邻接矩阵为n×n的矩阵（n为顶点总数）。
矩阵的元素aij（第i行，第j列）表示顶点vi与顶点vj之间的边总数，所得矩阵A=A(G)=(aij)n×n为图G的邻接矩阵。邻接矩阵可以描述有向图和无向图。
如图：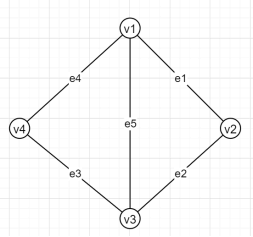

所得的邻接矩阵为：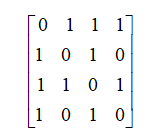

邻接矩阵的存储特点：
（a）无向图的邻接矩阵一定是一个对称矩阵，有向图不一定是。
（b）邻接矩阵所需的存储空间值域只与顶点数有关系。
（c）用邻接矩阵存储图，容易判断两个点之间是否有边。
（d）如果一个有向图的邻接矩阵为三角矩阵（主对角线为0），则它的拓扑排序一定存在。
（e）小技巧：
无向图：邻接矩阵的第i行或者第i列的非零元素的个数正好是第i个顶点Vi的度；
有向图：邻接矩阵的第i行的非零元素个数正好是第i个顶点Vi的出度，第i列非零元素的个数正好是第i个顶点Vi的入度。

1.4 关联矩阵

设任意图G=(V,E)，其中顶点集V=v1,v2,…,vm，边集E=e1,e2,…,en。
该图的关联矩阵为m×n的矩阵（m为顶点总数，n为边总数）。
矩阵的元素aij（第i行，第j列）表示顶点vi与边ej关联的关系，可能取值为0,1，-1，称所得矩阵M(G)=(mij)m×n为图G的关联矩阵。
aij取值说明：
0：表示vi与ej没有关系。
1：表示vi是ej的起点。
-1：表示vi是ej的终点。
如图：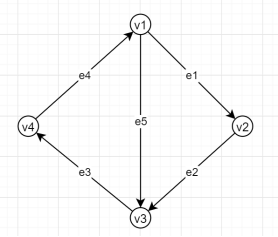

得到的关联矩阵为：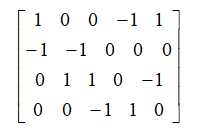

1.5 连通图和连通分量

连通图：无向图中，若从顶点u到顶点v有路径，称为u，v是连通的。若图中任意两个顶点均是连通的，则称为连通图。
连通分量：无向图中极大连通子图称为连通分量，也就是一个图中有多块图，每一块连通着就是一个连通分量。
比如下图，两个图没有连通，这个图是非连通图，但是两个子图是连通的，这两个子图称为连通分量。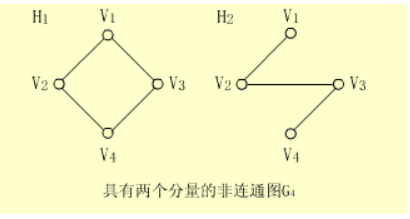

1.6 强连通图和强连通分量

强连通图：有向图中，若从顶点u到顶点v有路径，称为u，v是连通的。若图中任意两个顶点均是连通的，则称为强连通图。
强连通分量：有向图的极大强连通子图称为G的强连通分量。也就是一个图中有多块图，每一块连通着就是一个强连通分量。
特点：强连通图只有强连通分量（本身），非强连通图有多个强连通分量。
如下图，图中的G1不是强连通图，因为v3到v2没有路径，但它有两个强连通分量：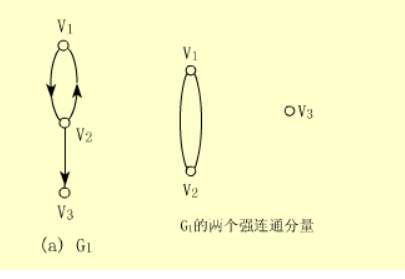

参考：关于有向图、无向图、邻接矩阵、关联矩阵、连通分量的概念详见以下两篇博客：
https://blog.csdn.net/weixin_42662955/article/details/89286893
https://blog.csdn.net/weixin_30569153/article/details/99390963

1.7 网络

权：表示两点之间具有意义的数字。
网络：带权的图就叫做网络图。