树

树的定义

树可以被递归的定义为一些节点的集合。这个集合可以是空集；若不是空集，则树由根节点及0个或多个非空（子）树组成，每个子树的根（儿子）都被来自根节点（父亲）的一条有向边连结。一棵树是N个节点和N-1条边的集合，其中的一个节点叫作根。没有儿子的节点成为树叶，具有相同父亲的节点为兄弟。
两个节点间路径的长为该路径上边的条数，对任意节点的深度为根到该节点唯一路径的长，根的深度为0.
节点的高是到一片树叶的最长路径的长，树叶的高都是0。

树的实现

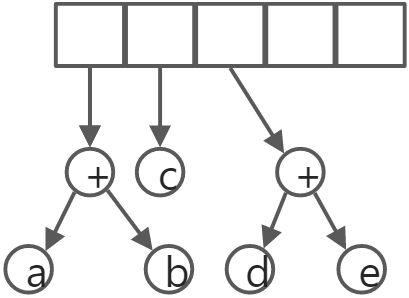
实现树可以在每个节点除数据外还保存到其他节点的链。

  1. class TreeNode
  2. {
  3.     Object element;
  4.     TreeNode firstChild;
  5.     TreeNode nextSibling;
  6. }

树的遍历

先序遍历：对节点的处理工作在他的诸儿子节点被处理之前进行。
后序遍历：节点的工作在诸儿子节点被计算后进行。

二叉树

二叉树每个节点都不能有多于两个的儿子。
二叉树的一个性质是：一颗平均二叉树的深度要比节点个数N小得多。

表达式树

表达式树的树叶是操作数（常数或变量名），其他节点为操作符。若所有操作符都是二元的，则刚好构成一个二叉树。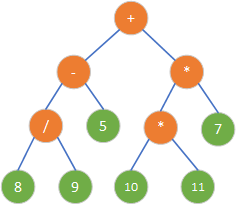
image.png
中序遍历：可以通过递归的产生一个带括号的左表达式，打印出在根处的运算符，再递归的产生一个带括号的右表达式而得到一个中缀表达式。

中缀表达式（或中缀记法）是操作符以中缀形式处于操作数中间（例：3+4），与前缀或后缀不同的是，中缀里必须用括号将操作符和对应的操作数括起来指示运算次序。
前缀表达式：- +8 4 6 2
中缀表达式：8+4-62
后缀表达式：8 4+6 2* -

先序遍历：先打印出运算符，然后递归的打印出右子树和左子树，得到前缀表达式。
后序遍历：递归的打印出左子树、右子树，然后打印运算符，得到后缀表达式。

构造表达式树

设输入为

前两个符号是操作数，因此创建两颗单节点树并将它们压入栈中。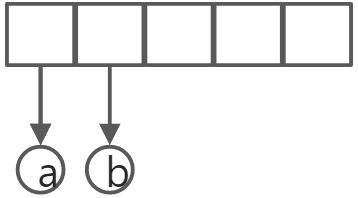
树 - 图2
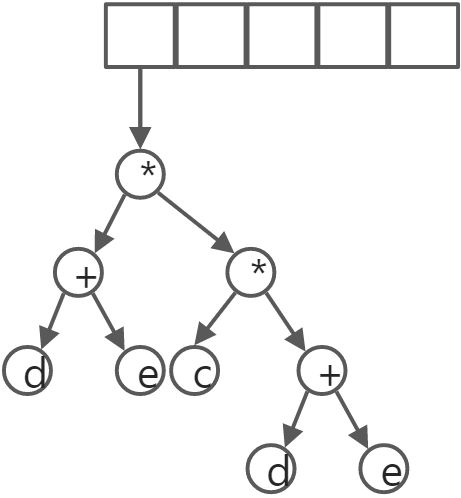
接着‘+’被读入，因此两棵树被弹出，一颗新树形成并被压入栈中。

树 - 图3

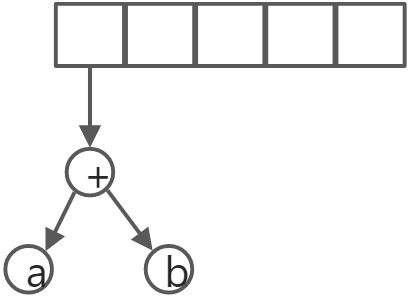
c、d、e被读入，在单个节点树创建后同样被压入栈中。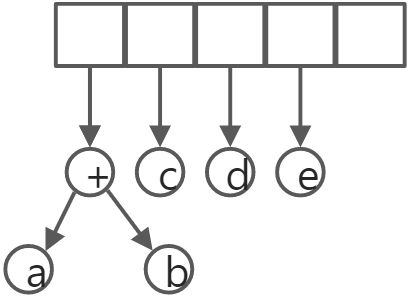
树 - 图4
接下来读入‘+’号，两棵树合并。

树 - 图5
继续读入‘’号和‘’号，所有树合并，最后的树被留在栈中。
树 - 图6

查找树ADT-二叉查找树

AVL树

伸展树

标准库中的集合与映射