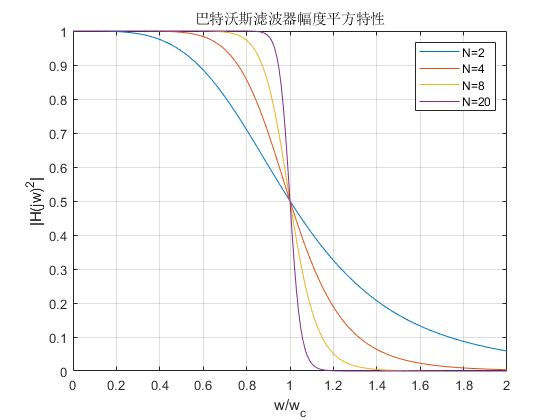
模拟低通巴特沃斯滤波器，其幅度平方函数为：
巴特沃斯滤波器 - 图1

  1. n=0:0.01:2;
  2. N=[2 4 8 20];
  3. for i=1:4
  4.     [z,p,k] = buttap(N(i));
  5.     [b,a] = zp2tf(z,p,k); %将零极点增益滤波器参数转换为传递函数的形式
  6.     [H,w] = freqs(b,a,n); %返回一个模拟滤波器的H(jw)的复频域响应（拉普拉斯格式）
  7.     magH(i,:) = (abs(H)).^2;
  8.     plot(w,magH(i,:));
  9.     hold on
  10. end
  12. legend(['N=',num2str(N(1))],['N=',num2str(N(2))],['N=',num2str(N(3))],...
  13.     ['N=',num2str(N(4))])
  15. xlabel('w/w_c')
  16. ylabel('|H(jw)^2|')
  17. title('巴特沃斯滤波器幅度平方特性')
  18. grid on
  19. ylim([0,1])

巴特沃斯滤波器幅度平方特性.png

设计例题

待设计的模拟滤波器技术指标为：巴特沃斯滤波器 - 图3,巴特沃斯滤波器 - 图4,巴特沃斯滤波器 - 图5,巴特沃斯滤波器 - 图6，设计合适的巴特沃斯滤波器。

Fs=20000; %采样率
wp=2000; %通带截止频率
ws=5000; %阻带截止频率
Rp=5; %通带最大衰减
As=40; %阻带最小衰减
[n,Wn] = buttord(wp/(Fs/2),ws/(Fs/2),Rp,As); %%计算butterworth滤波器的阶数以及3dB截止频率
%buttord函数中的wp与ws均为归一化值，取值范围在[0 , 1]之间
[b,a] = butter(n,Wn);%butter生成一个n阶的巴特沃斯滤波器，Wn为3dB截止频率
[H,W] = freqz(b,a); %freqz是滤波器频率响应函数，分别返回幅值响应和相位响应
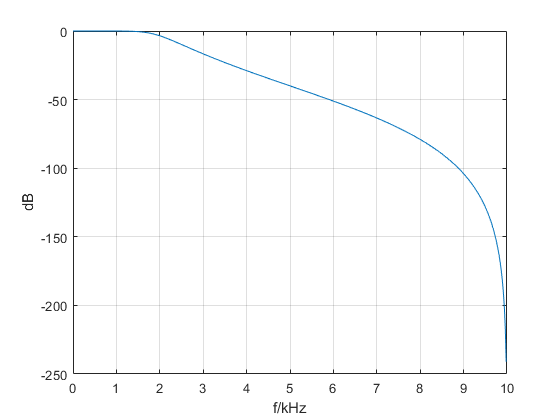
plot(W*Fs/(2*pi)/1000,20*log10(abs(H)));
ylabel('dB')
xlabel('f/kHz')
grid on

li1.png