基础课程 - 15 数据结构 - 《JavaSE》

一、什么是数据结构
二、数据结构分类
三、线性数据结构
四、非线性数据结构

一、什么是数据结构

数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。通常情况下，精心选择的数据结构可以带来更高的运行或者存储效率。数据结构往往同高效的检索算法和索引技术有关。

可视化：https://www.cs.usfca.edu/~galles/visualization/Algorithms.html

二、数据结构分类

数据结构一般来说按照存储结构细分为数组、链表、栈、队列、树、图、等等，如果按照逻辑结构来就简单分为线性和 非线性。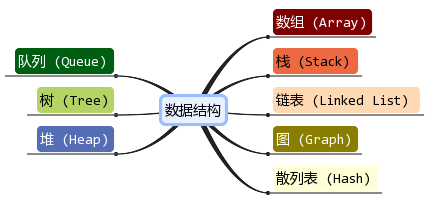
15 数据结构 - 图1
线性结构，指的是数据元素之间存在着“一对一”的线性关系的数据结构，存在一个绝对的前一个元素和最后一个元素，且每个元素都只存在一个唯一的前驱和后后继元素。
非线性结构，数学用语，其逻辑特征是一个结点元素可能有多个直接前驱和多个直接后继。

三、线性数据结构

3.1 数组

数组是一种基础的线性数据结构，一个数组的内存空间在物理上是连续的，通过首地址偏移来寻址元素。

一维数组示意图：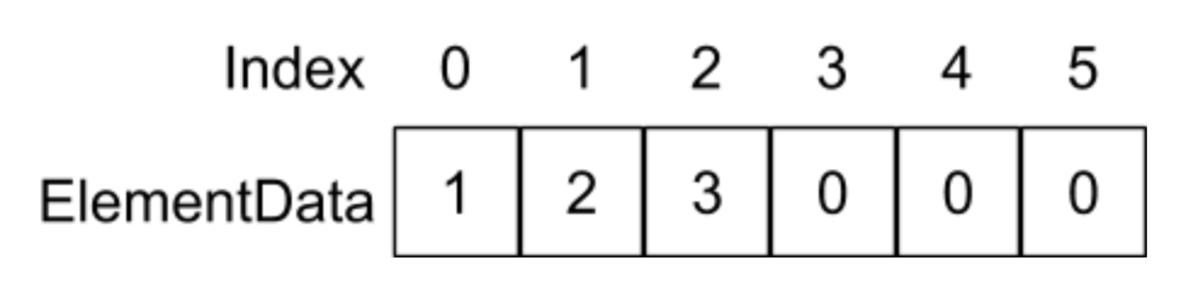
15 数据结构 - 图2

二维数组不是线性数据结构。

ArrayList Vector 均采用数组作为底层存储数据的结构

public class ArrayList<E> extends AbstractList<E>
        implements List<E>, RandomAccess, Cloneable, java.io.Serializable
{
    private static final long serialVersionUID = 8683452581122892189L;
    /**
     * 默认初始化容量
     */
    private static final int DEFAULT_CAPACITY = 10;
    /**
     默认数组。
     */
    private static final Object[] DEFAULTCAPACITY_EMPTY_ELEMENTDATA = {};
    /**
     存放数据的数组  
     */
    transient Object[] elementData; // non-private to simplify nested class access
    /**
     记录元素存放的个数
     */
    private int size;
}

   public boolean add(E e) {
        //确保数字的容量足够
        ensureCapacityInternal(size + 1);  // Increments modCount!!
        elementData[size++] = e;
        return true;
    }
    private void ensureCapacityInternal(int minCapacity) {
        ensureExplicitCapacity(calculateCapacity(elementData, minCapacity));
    }
    //计算最低需要的空间
    private static int calculateCapacity(Object[] elementData, int minCapacity) {
        if (elementData == DEFAULTCAPACITY_EMPTY_ELEMENTDATA) {
            return Math.max(DEFAULT_CAPACITY, minCapacity);
        }
        return minCapacity;
    }
   //扩容
   private void ensureExplicitCapacity(int minCapacity) {
        modCount++;
        // overflow-conscious code
        if (minCapacity - elementData.length > 0)
            grow(minCapacity);
    }
    //扩容逻辑
    private void grow(int minCapacity) {
        // overflow-conscious code
        int oldCapacity = elementData.length;
        int newCapacity = oldCapacity + (oldCapacity >> 1);
        if (newCapacity - minCapacity < 0)
            newCapacity = minCapacity;
        if (newCapacity - MAX_ARRAY_SIZE > 0)
            newCapacity = hugeCapacity(minCapacity);
        // minCapacity is usually close to size, so this is a win:
        elementData = Arrays.copyOf(elementData, newCapacity);
    }

3.2 链表

链表是一种物理存储单元上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列结点（链表中每一个元素称为结点）组成，结点可以在运行时动态生成。每个结点包括两个部分：一个是存储数据元素的数据域，另一个是存储下一个结点地址的指针域。相比于线性表顺序结构，操作复杂。由于不必须按顺序存储，链表在插入的时候可以达到O(1)的复杂度，比另一种线性表顺序表快得多，但是查找一个节点或者访问特定编号的节点则需要O(n)的时间，而线性表和顺序表相应的时间复杂度分别是O(logn)和O(1)。

单向和双向连表:

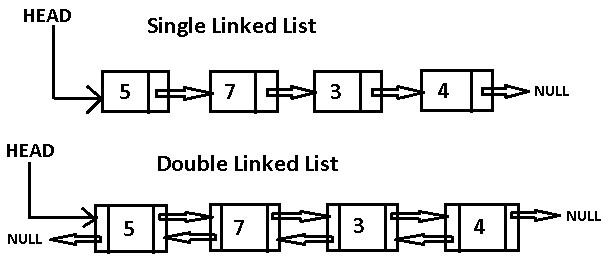
15 数据结构 - 图3

LinkedList 底层使用双向连表结构

    private static class Node<E> {
        E item;
        Node<E> next;
        Node<E> prev;
        Node(Node<E> prev, E element, Node<E> next) {
            this.item = element;
            this.next = next;
            this.prev = prev;
        }
    }

    void linkLast(E e) {
        final Node<E> l = last;
        final Node<E> newNode = new Node<>(l, e, null);
        last = newNode;
        if (l == null)
            first = newNode;
        else
            l.next = newNode;
        size++;
        modCount++;
    }

3.3 栈

栈（stack）又名堆栈，它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶，相对地，把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。

栈结构示意图：

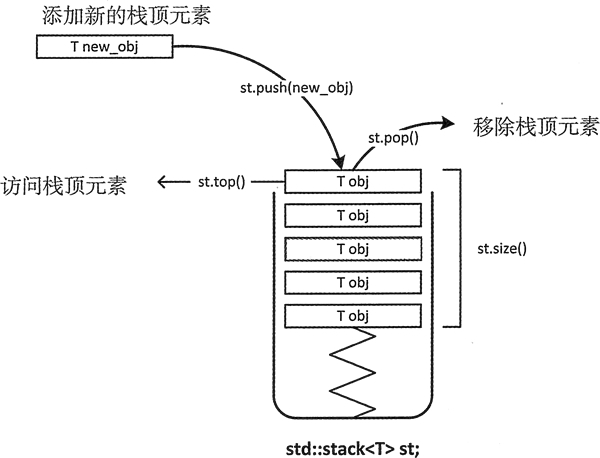
15 数据结构 - 图4

后进先出 F I L O

Java Stack 通过Vector实现。

3.4 队列

队列是一种特殊的线性表，特殊之处在于它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操作，和栈一样，队列是一种操作受限制的线性表。进行插入操作的端称为队尾，进行删除操作的端称为队头。

队列示意图：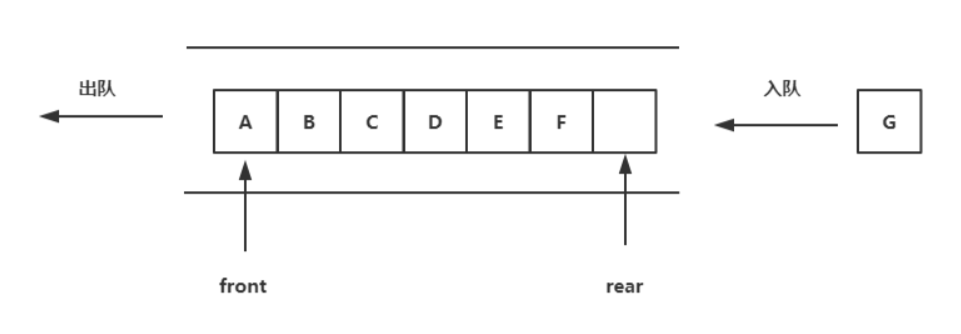

该结构的特点是先进先出 FIFO

Java 集合中 LinkedList 实现了队列的功能

入队列，添加到链表尾部
public boolean add(E e) {
        linkLast(e);
        return true;
}
出队列，从链表头部移除
public E poll() {
        final Node<E> f = first;
        return (f == null) ? null : unlinkFirst(f);
}

remove() 获取并移除但是如果队列空了就抛出异常

四、非线性数据结构

4.1 树(Tree)

树是一种数据结构，它是由n(n≥1)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点：

每个节点有零个或多个子节点；
没有父节点的节点称为根节点；
每一个非根节点有且只有一个父节点；
除了根节点外，每个子节点可以分为多个不相交的子树。

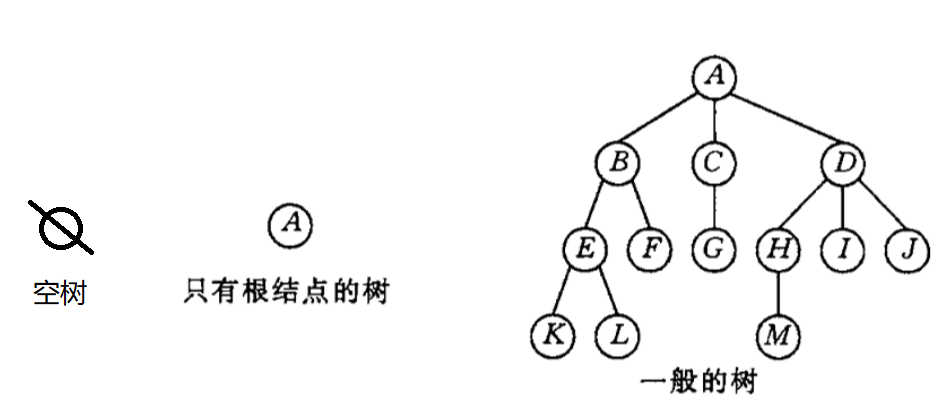
15 数据结构 - 图6

4.2 二叉树(Binary Tree)

二叉树（binary tree）是指树中节点的度不大于2的有序树，它是一种最简单且最重要的树。二叉树的递归定义为：二叉树是一棵空树，或者是一棵由一个根节点和两棵互不相交的，分别称作根的左子树和右子树组成的非空树；左子树和右子树又同样都是二叉树

15 数据结构 - 图7

4.3 二叉查找树(Binary Serarch Tree) 又称二叉搜索树

二叉搜索树是一种节点值之间具有一定数量级次序的二叉树，对于树中每个节点：

若其左子树存在，则其左子树中每个节点的值都不大于该节点值；
若其右子树存在，则其右子树中每个节点的值都不小于该节点值。

15 数据结构 - 图8

二叉树遍历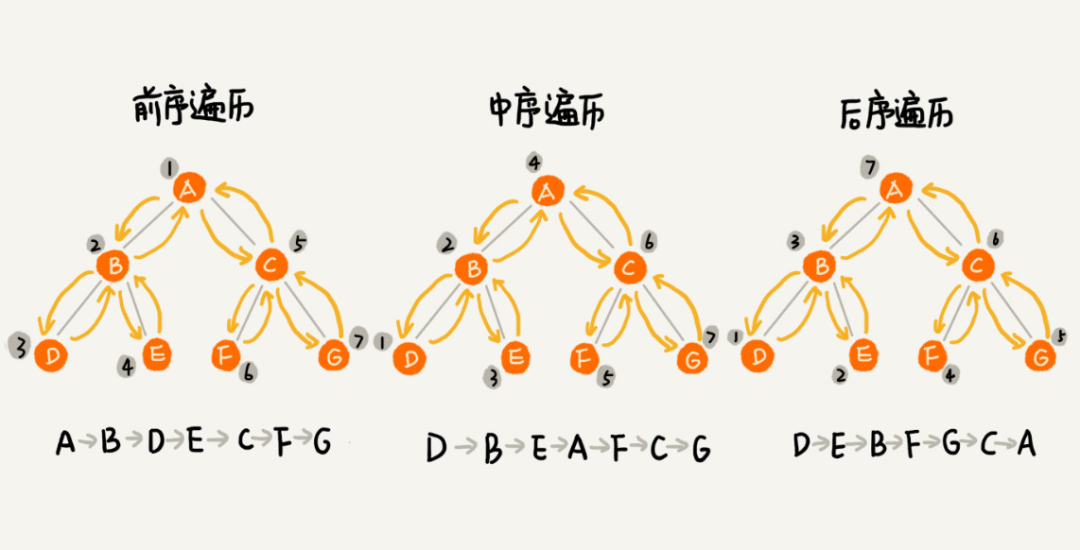

4.4 二叉平衡查找树(self-balancing binary search tree)

AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1，所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis，他们在1962年的论文《An algorithm for the organization of information》中发表了它

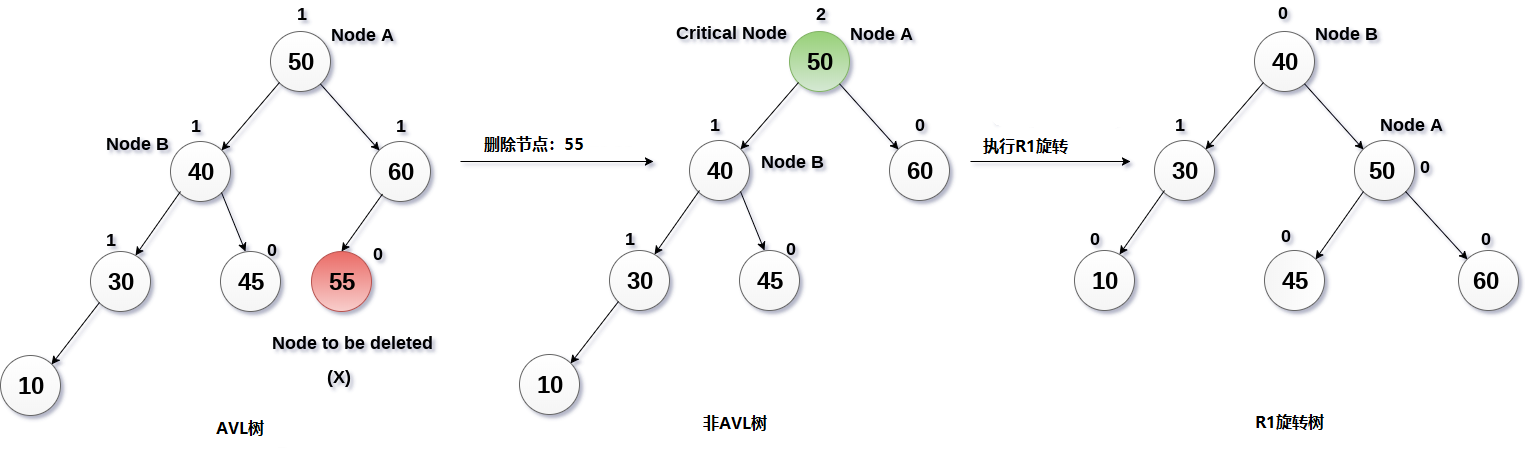
15 数据结构 - 图10

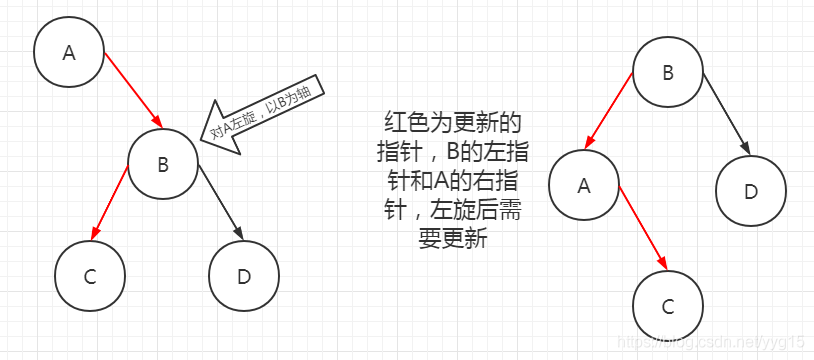
左旋右旋操作：

左旋：对X节点左旋，即以X的右子树Y为轴，将X节点转下来，变为Y的左子树，
简单记为左旋即把该节点变为左子树。
右旋：对X节点右旋，即以X的左子树Y为轴，将X节点转下来，变为Y的右子树，
简单记为右旋即把该节点变为右子树。

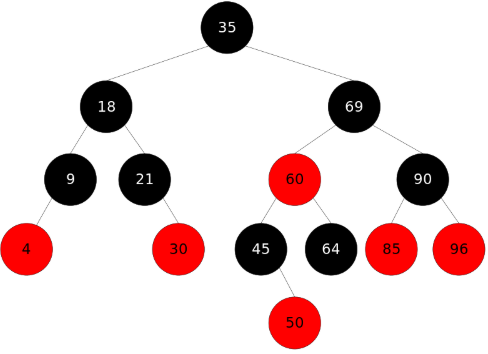
4.5 红黑数( Red-Black Tree )

红黑树是一种特定类型的二叉树，它是在计算机科学中用来组织数据比如数字的块的一种结构。红黑树是一种平衡二叉查找树的变体，它的左右子树高差有可能大于 1，所以红黑树不是严格意义上的平衡二叉树（AVL），但对之进行平衡的代价较低，其平均统计性能要强于 AVL 。由于每一棵红黑树都是一颗二叉排序树，因此，在对红黑树进行查找时，可以采用运用于普通二叉排序树上的查找算法，在查找过程中不需要颜色信息。

要求：

每个节点非红即黑
根节点是黑的;
每个叶节点（叶节点即树尾端NULL指针或NULL节点）都是黑的;
如图所示，如果一个节点是红的，那么它的两儿子都是黑的;
对于任意节点而言，其到叶子点树NULL指针的每条路径都包含相同数目的黑节点;
每条路径都包含相同的黑节点;

红黑树示意图：

15 数据结构 - 图12

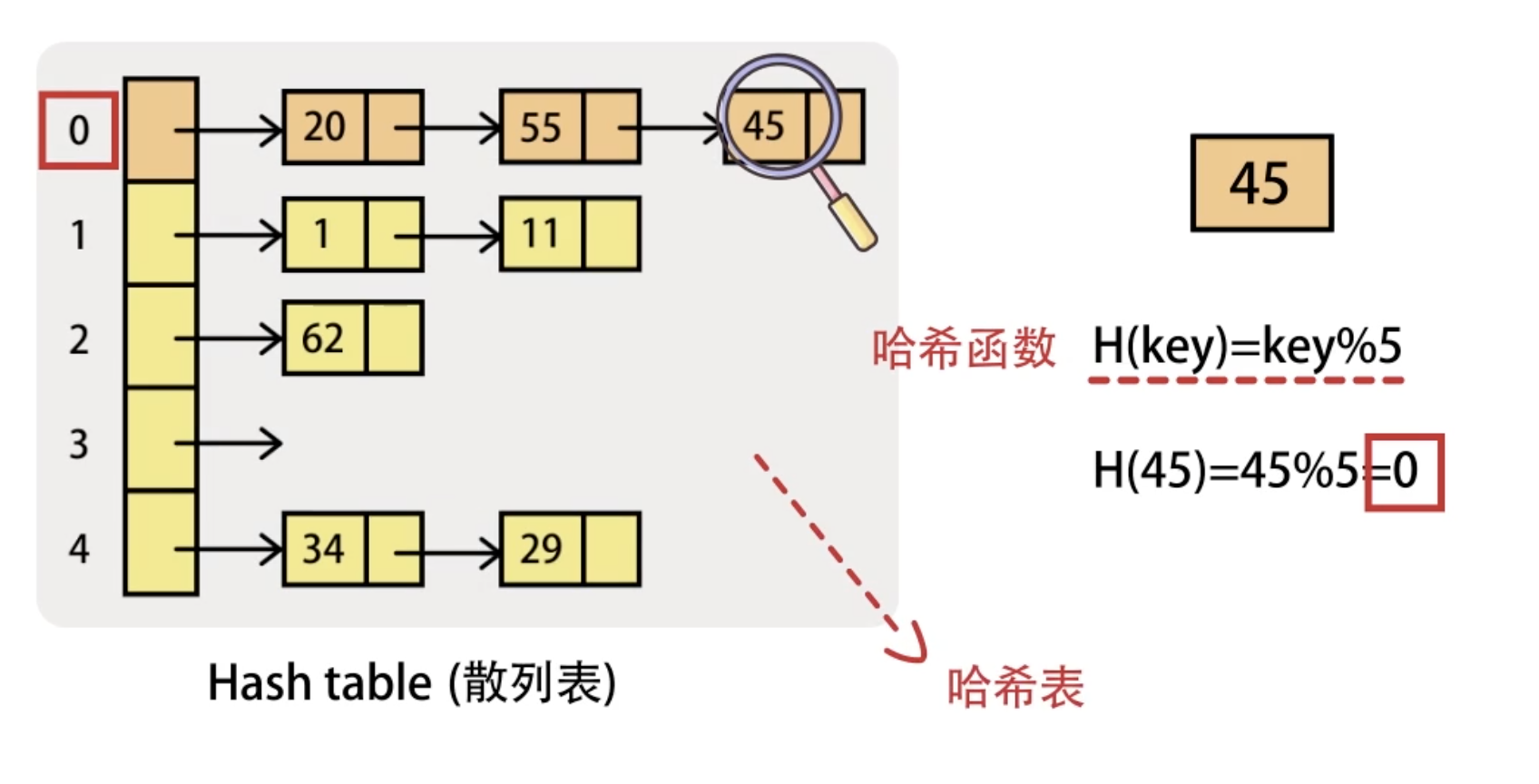
4.6 散列表结构( HashTable )

hash表示意图：

15 数据结构 - 图13

 final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
                   boolean evict) {
        Node<K,V>[] tab; Node<K,V> p; int n, i;
        // 如果当前hashtable 为null 
        if ((tab = table) == null || (n = tab.length) == 0)
            // 初始化hashtable 返回了底层hashtable   
            n = (tab = resize()).length;
        //  通过生成hashcode 判断 此位置是否为null
        if ((p = tab[i = (n - 1) & hash]) == null)
            //如果为空直接保存
            tab[i] = newNode(hash, key, value, null);
        else {
            //此位置有人,且key相同
            Node<K,V> e; K k;
            if (p.hash == hash &&
                ((k = p.key) == key || (key != null && key.equals(k))))
                e = p;
            // key 不同，如果这里是一个红黑树，添加到树上
            else if (p instanceof TreeNode)
                e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
            else {
                // 这里存在的元素是一个链表，添加链表尾部
                for (int binCount = 0; ; ++binCount) {
                    //找到了末尾
                    if ((e = p.next) == null) {
                        //元素添加到末尾
                        p.next = newNode(hash, key, value, null);
                        // 如果链表长度超过8 把链表转成红黑树(添加次数可能很多，使用红黑树效率更好)
                        if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
                            treeifyBin(tab, hash);
                        break;
                    }
                    //寻找过程中如果和链表中的某个节点和添加的重复放弃存储
                    if (e.hash == hash &&
                        ((k = e.key) == key || (key != null && key.equals(k))))
                        break;
                    // 
                    p = e;
                }
            }
            //如果添加的key存在则覆盖以前的值，并返回被覆盖的旧的值。
            if (e != null) { // existing mapping for key
                V oldValue = e.value;
                if (!onlyIfAbsent || oldValue == null)
                    e.value = value;
                afterNodeAccess(e);
                return oldValue;
            }
        }
        ++modCount;
        if (++size > threshold)
            resize();
        afterNodeInsertion(evict);
        return null;
    }


分类树结构
                   [   千锋北京总部    ]
           重庆         成都    西安      广州
      石桥铺   杨家坪
【  ID  名字  父级ID  】
    1   数码    0
    2   手机    1
    3   相机    1
    4   单反    3
    5   交卷    3
    6   智能手机 2
    7   华为    6
    8   Vivo    6
                      数码
           手机                 相机
      智能手机                单反    交卷  
  华为    vivo              
clss Node{
    id
    name
    pid
    List<Node> child;
}