题目信号

  • 下一个更大/小的
  • 固定区间内最值
  • 单调栈适合的题目是求解「第一个一个大于 xxx」或者「第一个小于 xxx」这种题目。所有当你有这种需求的时候，就应该想到单调栈。
  • https://zhuanlan.zhihu.com/p/273400551
  • 这四道题都是删除或者保留若干个字符，使得剩下的数字最小（或最大）或者字典序最小（或最大）

后面第一个比我大的

  • 正向遍历数组
  • 从头至尾单调递减（因为遇到小的弹出，遇到大于等于的停下，所以从头到尾递减）
  • 遇到比自己小的弹出，此时被弹出元素找到后面第一个比他大的
  • 最后队列中剩下的元素就是后面没有比他大的

后面第一个比我小的

  • 正向遍历数组
  • 从头到尾单调递增（因为遇到大的弹出，遇到小于等于的停下，所以从头到尾递增）
  • 遇到比自己大的弹出，此时被弹出元素找到后面第一个比他小的
  • 最后队列中剩下的元素就是后面没有比他小的

前面第一个比我大的

  • 反向遍历数组 + 后面第一个比我大的 一样的做法

前面第一个比我小的

题型

基础队列

341. 扁平化嵌套列表迭代器（Done）

  • DFS遍历+按照DFS顺序插入队列

  • 按照队列中的顺序，从头弹出就行。

    剑指 Offer 50. 第一个只出现一次的字符 (Done)

    答案：

  • 维护一个HashMap来判断是否重复

  • 维护一个队列来保存第一个不重复字符，里面存char
  • 遍历数组
    • 若该字符没出现，加入map，加入队列的尾端
    • 若出现过，更新map中字符的value为-1，来表示该字符已经重复。开始检查队列的头部，如果头部是重复的（map中value为-1）弹出头部。直到队列为空或者头部不重复为止

  • 如果队列为空则返回‘ ’，反之返回队列头部字符。

    622. 设计循环队列 (Done)

    这题的意义在于，自己用数组实现一个队列。
    答案：

  • 维护三个数值

    • currSize
    • headIndex -> 指向队列头部的索引
    • taillindex -> 指向下一个可被加入的索引，目前队尾元素=tailIndex-1

  • enQueue

    1. public boolean enQueue(int value) {
    2.   if (currSize < size){
    3.       queue[tailIndex%size] = value;
    4.       tailIndex++;
    5.       currSize++;
    6.       return true;
    7.   }
    8.   return false;
    9. }

  • deQueue

    public boolean deQueue() {
  if (currSize == 0) return false;
  headIndex++;
  currSize--;
  if (currSize == 0){
      headIndex = 0;
      tailIndex = 0;
  }
  return true;
}

  • Front & Rear ```java public int Front() { if (currSize == 0) return -1; return queue[headIndex%size]; }

public int Rear() { if (currSize == 0) return -1; return queue[(tailIndex-1)%size]; }

<a name="lVBBr"></a>
## 单调队列
模版

- 反向遍历数组
- 根据deque是否为空来判断是否有和法值

<a name="m85HO"></a>
#### [239. 滑动窗口最大值](https://leetcode-cn.com/problems/sliding-window-maximum/)(Done)

- 用双端队列实现最大队列，最大值在队头
- offer
   - 和队列最后一个比较，如果比他大，弹出队列最后一个。直到队列为空或者最后一个大于等于将要插入的元素
   - 插入元素
- poll
   - 如果要移除的元素，等于队头，则弹出队头
<a name="XVz6z"></a>
#### [剑指 Offer   59 - II. 队列的最大值](https://leetcode-cn.com/problems/dui-lie-de-zui-da-zhi-lcof/)（Done）

- 就是用一下deque实现最大队列，类似503更为简单。
<a name="dUxmk"></a>
#### [739.   每日温度](https://leetcode-cn.com/problems/daily-temperatures/)(Done)

- 和503类似，更加简单。    
<a name="kdGBF"></a>
#### [496. 下一个更大元素   I](https://leetcode-cn.com/problems/next-greater-element-i/)(Done)

- 用Deque实现单调队列
- 先反向遍历nums2，同时维护一个hashmap。
   - 对于每一个num，我们在把他插入单调队列之前可以判断有没有比他大的元素以及有的话第一个是什么。
- 然后遍历nums1，从hashmap中找出对应的答案
<a name="S3ICd"></a>
#### [503. 下一个更大元素   II](https://leetcode-cn.com/problems/next-greater-element-ii/)(Done)

- 用Deque实现单调队列
- 因为为循环队列，我们需要反向循环数组两次
- 相当于把数组接在自己后面，就模拟了循环 -> nums + nums
   - 第一次, 为了从尾到头的递增队列，从而可以得到在每个元素右边的所有元素的信息，从而判断是否有下一个更大的元素。
   - 第二次，找出答案。
<a name="EVaCF"></a>
#### [1438. 绝对差不超过限制的最长连续子数组](https://leetcode-cn.com/problems/longest-continuous-subarray-with-absolute-diff-less-than-or-equal-to-limit/)（Done）

- 滑动窗口+两个单调队列（maxQueue和minQueue）
- 答案
   - 需要知道窗口中的最大最小值，就可以判断新加一个值之后，新的窗口是不是有效窗口。

<a name="mqFJ6"></a>
#### [862. 和至少为 K 的最短子数组](https://leetcode-cn.com/problems/shortest-subarray-with-sum-at-least-k/)（Done）
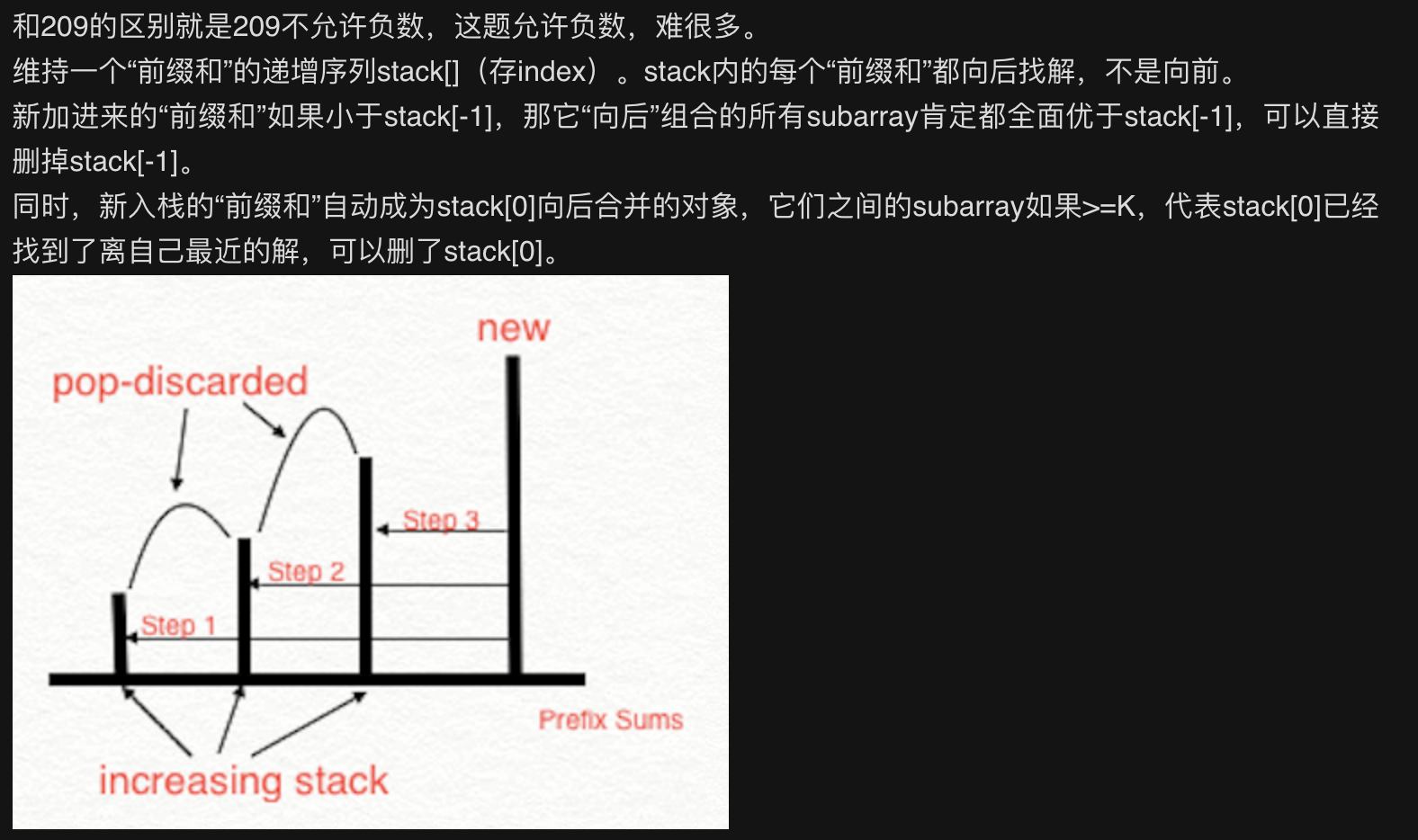
![Screen Shot 2021-07-03 at 4.48.19 pm.png](https://cdn.nlark.com/yuque/0/2021/png/21548627/1625302104914-12fe1e53-f428-40b9-ad4a-292acaba025d.png#clientId=u7249d220-fc1b-4&from=drop&id=u814a6040&margin=%5Bobject%20Object%5D&name=Screen%20Shot%202021-07-03%20at%204.48.19%20pm.png&originHeight=934&originWidth=1576&originalType=binary&ratio=1&size=583158&status=done&style=none&taskId=u8889c025-06f8-41e6-b271-c285d1a5868)

- 答案
   - prefiix第一个是0，后面是剩下的前缀和
   - 使用头部是max的maxQueue来存储prefix对应的index
   - 循环全部前缀和数组
      - 先判断新的前缀和可否是队列头部元素>=k，若可这便是最小值。循环直到队列为空，或者不满足构成答案的条件。
      - 接下来，看队列尾部。若尾部大于等于当前的前缀和，弹出尾部。因为当前的前缀和的答案肯定比这个尾部更短。循环直到队列为空，或者不满足条件。
      - 将新的前缀和加入队列尾部。

<a name="HDv1O"></a>
## 栈的转化
<a name="DnpJz"></a>
#### [232. 用栈实现队列](https://leetcode-cn.com/problems/implement-queue-using-stacks/)(Done)

- 一个in stack，一个 out stack
- 当out stack为空时，将 in stack 倒出来 装进 out。
<a name="cDdYc"></a>
#### [225. 用队列实现栈](https://leetcode-cn.com/problems/implement-stack-using-queues/)(Done)

- 两个队列的方法
   - push的时候，把元素放在queue2的第一个，然后把queue1的元素一个一个放进queue2，这样子新进来的元素永远在队列的首位了。
```java
public void push(int x) {
    queue2.offer(x);
    while (!queue1.isEmpty()) {
        queue2.offer(queue1.poll());
    }
    Queue<Integer> temp = queue1;
    queue1 = queue2;
    queue2 = temp;
}
  • 一个队列的方法
    • push的时候，先获取当前队列长度n。
    • 将新元素放入队列尾部
    • 然后将他前面n个元素一个一个的放到新元素的后面
      public void push(int x) {
int n = queue.size();
queue.offer(x);
for (int i = 0; i < n; i++) {
   queue.offer(queue.poll());
}
}

最小/大栈

155. 最小栈 (Done)

716. 最大栈 (Done)

  • 维护最大栈的时候和单调队列不一样

    public void push(int x) {
  stack.push(x);
  // 和单调队列不一样的，不会弹出以前的值，而是判断新值要不要加进去
  if (maxStack.isEmpty() || x >= maxStack.peek())
      maxStack.push(x);
}

    验证栈序列

    946. 验证栈序列(Done)

    Simulation

    int popIndex = 0;
// 依次push元素入栈
for (int elem : pushed){
  stack.push(elem);
  // 检查是否有可以出栈的元素，知道无法出栈为止
  while (!stack.isEmpty() && popIndex < popped.length && stack.peek() == popped[popIndex]){
      stack.pop();
      popIndex++;
  }
}
// 如果此时栈为空，则表示合法。
return stack.isEmpty();

    单调栈

    581. 最短无序连续子数组(Done)

  • 自己想了一个小时没做出来，后来看答案，我在正确的思路上面了，但是左右边界要分两次单调栈遍历求出来。

  • 答案：
    • 法一：排序
      • 将数组排序，然后和原数组对比
      • 如果不一样，则表明这个元素乱序。
      • 找出最左和最右乱序元素
      • 返回乱序长度 ```java int l = nums.length, r = -1; int[] sortedNums = nums.clone(); Arrays.sort(sortedNums); for (int i = 0; i < nums.length; i++){ if (nums[i] != sortedNums[i]){ l = Math.min(l, i); r = Math.max(r, i); } }

if (r == -1) return 0; return r - l + 1;


   - 法二：单调栈
      - 单调栈，正向找左边边界
      - 单调栈，反向找右边边界
<a name="n0kFN"></a>
#### [456. 132   模式](https://leetcode-cn.com/problems/132-pattern/) （Done）

- 反向遍历数组
- 维护从尾到头递增栈
- 弹出来的元素就是可以做为k的元素，因为被弹出来表示前面有比他大的元素了，就是说j 和 k 都找齐了，只剩下i了。我们维护k的最大值，一旦出现元素小于k，我们就找到了i，                                                这样子i < j < k && nums[i] < nums[k] < num[j]就出现了。
```java
public boolean find132pattern(int[] nums) {
    Stack<Integer> stack = new Stack<>();
    int k = Integer.MIN_VALUE;

    for (int i = nums.length - 1; i >= 0; i--){
        if (nums[i] < k)
            return true;
        while (!stack.isEmpty() && stack.peek() < nums[i]){
            k = Math.max(k, stack.pop());
        }
        stack.push(nums[i]);
    }
    return false;
}

402. 移掉 K 位数字 （Done）