写在前面:
索引对查询的速度有着至关重要的影响,理解索引也是进行数据库性能调优的起点。考虑如下情况,假设数据库中一个表有10^6条记录,DBMS的页面大小为4K,并存储100条记录。如果没有索引,查询将对整个表进行扫描,最坏的情况下,如果所有数据页都不在内存,需要读取10^4个页面,如果这10^4个页面在磁盘上随机分布,需要进行10^4次I/O,假设磁盘每次I/O时间为10ms(忽略数据传输时间),则总共需要100s(但实际上要好很多很多)。如果对之建立B-Tree索引,则只需要进行log100(10^6)=3次页面读取,最坏情况下耗时30ms。这就是索引带来的效果,很多时候,当你的应用程序进行SQL查询速度很慢时,应该想想是否可以建索引。
什么是索引:
- 是一种特殊的文件,文件里包含这对数据表里所有数据的引用指针。索引往往是存储在磁盘上的文件中的(可能存储在单独的索引文件中,也可能和数据一起存储在数据文件中)。
- 通俗的说,就是一本书的目录。当我们想要查询书中的一些知识,可以快速提供 该知识的所在位置。
- 是一种数据结构,以协助快速查询,更新数据库表中的数据。
索引的优缺点:
优点:
方便查询,大大加快数据检索的速度,提高性能。
缺点:
对表中的数据进行增删改的时候,索引需要维护,会降低执行效率。
空间方面,索引需要占用物理空间
索引类型:
- 主键索引
- 索引列中的值必须是唯一的,不允许有空值。
- 普通索引
- 唯一索引
- 索引列中的值必须是唯一的,但是允许为空值。
- 全文索引
- 空间索引
平衡二叉树
平衡二叉树 采用的是二分法思想,在做为二叉树的前提下,最主要的是左子树和右子树的层级最多相差 1。
因为这样,我i们可以通过左选择和右旋转,来保持二叉树的平衡。不会出现一棵树的高,一棵树低的情况。
使用平衡二叉查找树查询的性能接近于二分查找法,时间复杂度是 O(log2n)。查询id=6,只需要两次IO。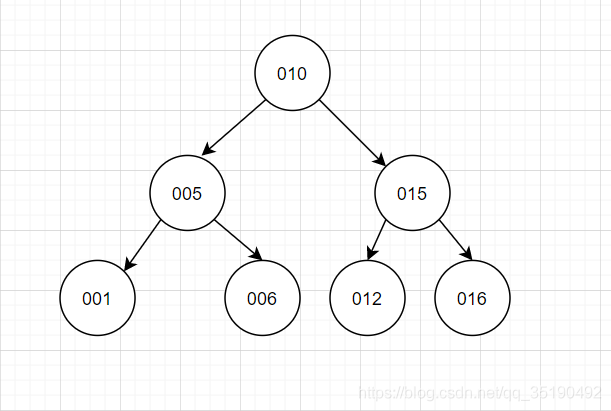
就这个特点来看,可能各位会觉得这就很好,可以达到二叉树的理想的情况了。然而依然存在一些问题:
- 时间复杂度和树高相关。树有多高就需要检索多少次,每个节点的读取,都对应一次磁盘 IO 操作。树的高度就等于每次查询数据时磁盘 IO 操作的次数。磁盘每次寻道时间为10ms,在表数据量大时,查询性能就会很差。(1百万的数据量,log2n约等于20次磁盘IO,时间20*10=0.2s)
- 平衡二叉树不支持范围查询快速查找,范围查询时需要从根节点多次遍历,查询效率不高。
BTree
在平衡二叉树中 ,假如 key 为8 个字节,然后每个指针4个字节,这样一个节点(8+2*4)16个字节。但是!!在MySQL的存储引擎是InnoDB,每次IO 会默认的读取一页(默认一页为16k)的数据量。这样,空间利用率超级低:16/16k 。=>0.1% 。所以我们要改造二叉树,增加空间利用率。
想法:在二叉树的每个节点上 ,存储多个元素。增加空间利用率。这就是B树。
B树的性质
- B树的节点中存储着多个元素,每个内节点有多个分叉。
- 节点中的元素包含键值和数据,节点中的键值从大到小排列。也就是说,在所有的节点都储存数据。
- 父节点当中的元素不会出现在子节点中。
- 所有的叶子结点都位于同一层,叶节点具有相同的深度,叶节点之间没有指针连接。
B树可优化的地方
看到这里一定觉得B树就很理想了,但是前辈们会告诉你依然存在可以优化的地方:
B树不支持范围查询的快速查找,你想想这么一个情况如果我们想要查找10和35之间的数据,查找到15之后,需要回到根节点重新遍历查找,需要从根节点进行多次遍历,查询效率有待提高。
如果data存储的是行记录,行的大小随着列数的增多,所占空间会变大。这时,一个页中可存储的数据量就会变少,树相应就会变高,磁盘IO次数就会变大。
解决方法:B+ 树
B+ 树
B+树和B树最主要的区别在于非叶子节点是否存储数据的问题.
- B树:非叶子节点和叶子节点都会存储数据。
- B+ 树: 只有叶子节点上,才能存储数据。而非叶子节点上,只存储key。叶子节点之间使用双向指针连接,最底层的叶子节点形成了一个双向有序链表。
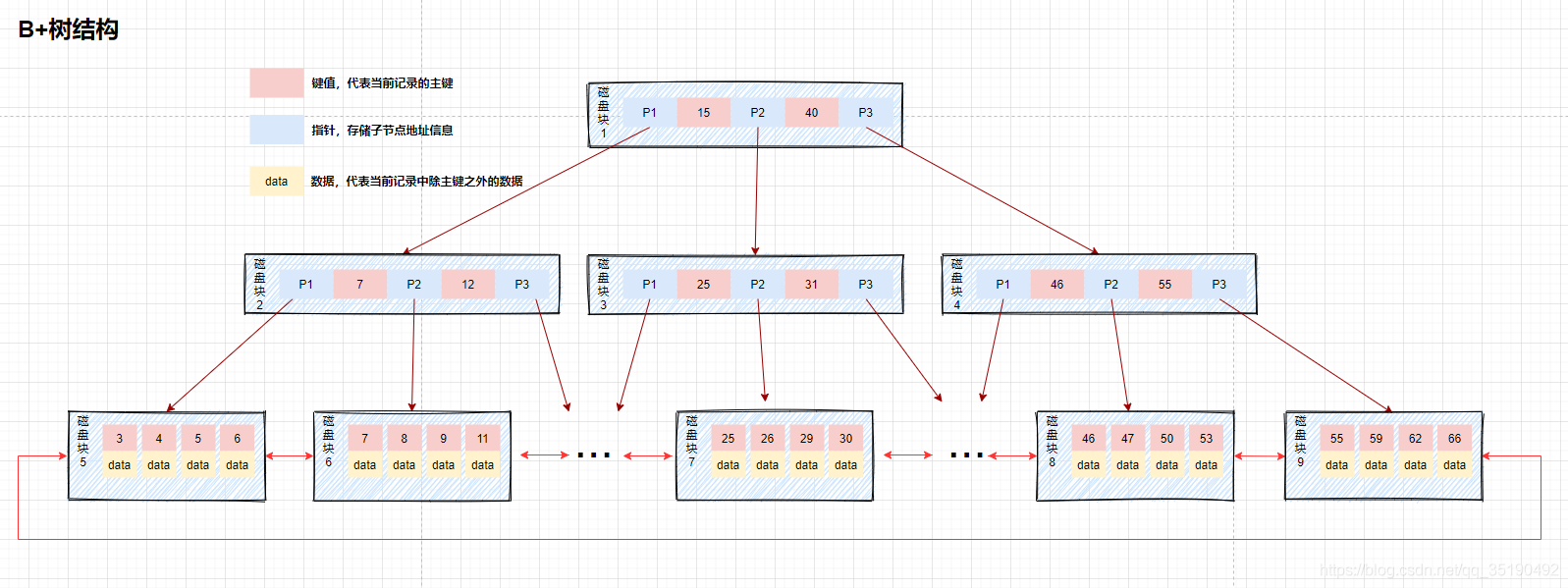
BTree 和B+Tree 的区别:
- 在B树中,可以将键和值都放在内部节点和叶子节点中;但是在B+树中,内部节点只能放键,没有值,叶子节点同时放键 和 值。
- B+树的叶子节点有一条链相连,而B树的叶子节点各自独立。
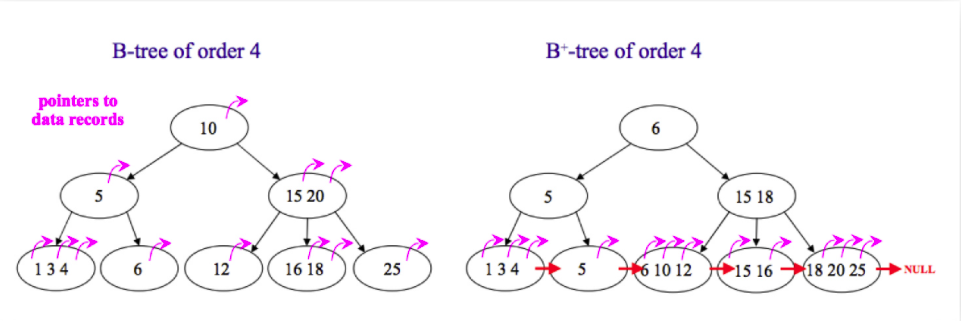
数据库为什么使用B+树:
- B+树适合随机检索和顺序检索。
- B+树的空间利用率较高,可以减少I/O次数,磁盘都的读写代价更低。
- B+树的查询效率更加稳定。

