完成日期：2021.07.11

Algorithm：70.爬楼梯

这首题算是动态规划中最经典，也是最简单的一道题了，一般题目的名称叫：小青蛙跳台阶。

这道题给我的最初印象是：递归，而且递归的代码也非常好写：

  1. def climbStairs(n: int) -> int:
  2.     if n == 1:
  3.         return 1
  4.     if n == 2:
  5.         return 2
  7.     return climbStairs(n-1) + climbStairs(n-2)

但这个的时间复杂度非常高，是，直接提交的话，力扣平台会直接按超时处理。为啥耗时这么长呢？
我们以10阶为例，要计算10阶，就要计算9阶和8阶，而要计算9阶，则需要计算8阶和7阶，以此类推的话，就会如下所示：
图中红色部分都是重复计算的部分，虽然每个部分的计算都只是加法，但无奈这是指数级的增加，很容易出现爆炸级增长的情况。
考虑到这里，其实最简单的思路就是把计算结果保留下来，每到一步只拿上次计算的结果加上即可。看着好像没有减少多少，但其实通过这样的优化后，上面的二叉树直接被剪枝成了一条链表！
具体的代码如下：

  1. memo = {}
  3. def getv(n):
  4.     if n in memo:
  5.         v = memo[n]
  6.     else:
  7.         v = climbStairs(n)
  8.         memo[n] = v
  9.     return v
  11. def climbStairs(n: int) -> int:
  12.     if n == 1:
  13.         return 1
  14.     if n == 2:
  15.         return 2
  17.     return getv(n-1) + getv(n-2)

另一种思路是动态规划，从思想上来看，动态规划是递归的逆向。

  • 递归是自顶向下，从最大的问题往下思考：10阶的问题可以看做9阶和8阶解法的和。
  • 动规是自底向上，从最小的问题往上思考：1阶有1种，2阶有2种，3阶则是1阶+2阶，……，10阶是8阶+9阶。

就本题而言，动规的解法如下：

  1. def climbStairs(n: int) -> int:
  2.     s1 = 1
  3.     s2 = 2
  4.     sn = 0
  5.     for i in range(3, n):
  6.         sn = s1 + s2
  7.         s1 = s2
  8.         s2 = sn
  9.     return sn

这种解法在题解里也有叫“滚动数组”的，这其实只是一种比较形象的叫法，其根本还是动态规划。
网上也搜到一些讲动规入门的，这篇我觉得讲的还是蛮清楚的。

不过说实话，动规还是蛮复杂的，主要是不好想那几个关键问题：

  • 拆分子问题
  • 最优子结构
  • 边界

后面要多刷几道该类型的题，锻炼思路了。

Review：无

Tips：无

Share：傅里叶变换

https://zhuanlan.zhihu.com/p/19763358

这篇里对于傅里叶变换和傅里叶级数算是讲的比较好的，主要是包含很多动图，把这两个概念讲的很清楚了。
特别是这张图，把很多概念都说明白了。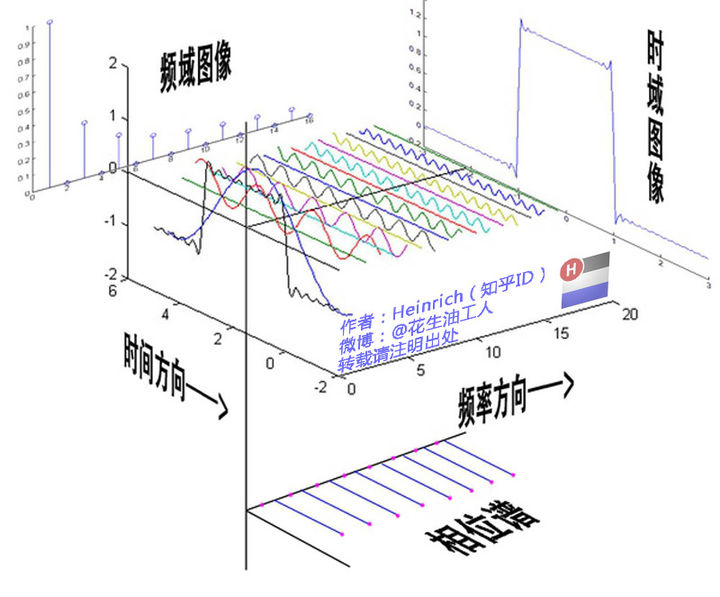
image.png
上图里：

  • 在时域中，x轴是时间，y轴是振幅
  • 在频域中，x轴是频率，y轴是振幅