1.数据结构

1.1数组

1.2链表

1.2.1 面试

（1）如何实现链表的反转？
答：使用头节点插入法。
1) 创建一个带头节点的链表
2) 定义一个循环链表变量p，p的初始值为待反转的链表
3) 遍历待反转的链表，遍历条件为 (p !=null)
a. 定义一个临时链表变量tempList保存p->next的值（因为p->next值会改变），用于下一次循环。
b. 把p当前指向的首节点和resultList链表的头节点之后的节点拼接起来。
c. 把b.步骤中拼接的节点 再拼接到resultList头节点后。
d. p重新赋值为3.1步骤中保存的tempList的值。
4) 返回resultList->next.即反转后的链表。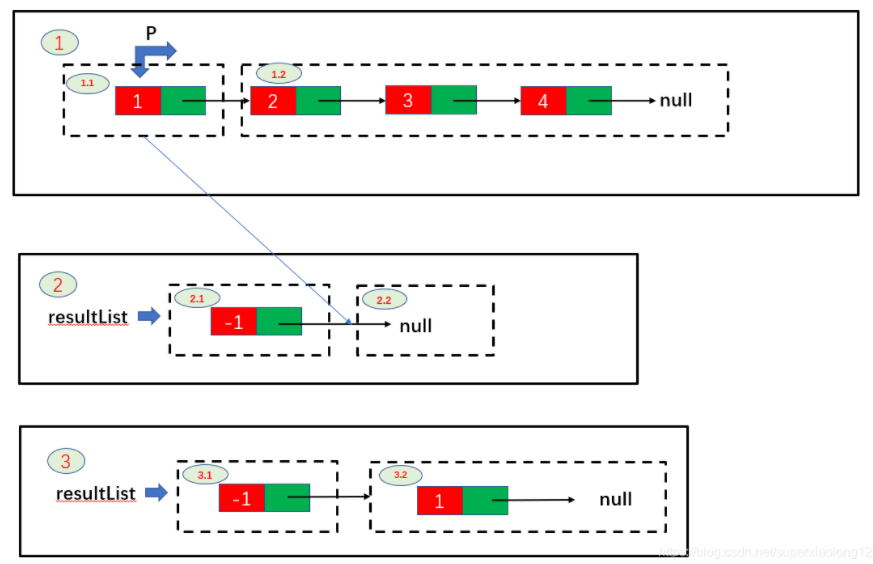
5--数据结构基础重难点 - 图1

1.3

2.基本排序算法

2.1 简介

常见的内部排序算法有：冒泡排序、选择排序、插入排序、希尔排序、快速排序、归并排序等。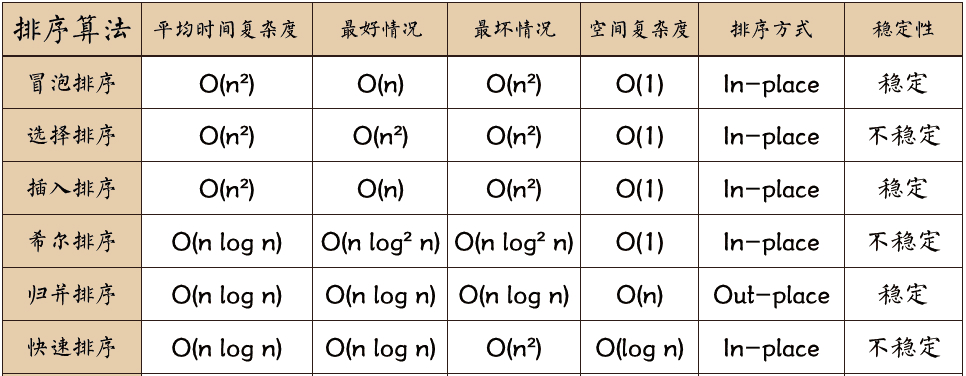
5--数据结构基础重难点 - 图2

2.2 代码实现

2.2.1 冒泡排序

5--数据结构基础重难点 - 图3
中心思想：越大的元素会经由交换慢慢“浮”到数列的顶端。
一共进行数组的大小 - 1 次大的循环
每一趟排序的次数逐渐减少
算法描述：
1. 是通过每一次遍历获取最大/最小值
2. 将最大值/最小值放在尾部/头部
3. 然后除开最大值/最小值，剩下的数据进行遍历获取最大/最小值
例子：5，3，2，4，8
3，2，4，5，8
2，3，4，5，8
2，3，4，5，8
代码：

  1. //基础冒泡
  2. public static void main(String[] args) {
  3.     int arr[] = {8, 5, 3, 2, 4};
  4.     for (int i = 0; i < arr.length-1; i++) {
  5.         //外层循环，遍历次数
  6.         for (int j = 0; j < arr.length - i - 1; j++) {
  7.             //内层循环，升序（如果前一个值比后一个值大，则交换）
  8.             //内层循环一次，获取一个最大值
  9.             if (arr[j] > arr[j + 1]) {
  10.                 int temp = arr[j + 1];
  11.                 arr[j + 1] = arr[j];
  12.                 arr[j] = temp;
  13.             }
  14.         }
  15.     }
  16.     System.out.println(Arrays.toString(arr));
  17. }
  18. //优化冒泡——加标志位
  19. public static void main(String[] args) {
  20.     int arr[] = {8, 5, 3, 2, 4};
  21.     int temp = 0;
  22.     boolean flag = false;
  23.     for (int i = 0; i < arr.length-1; i++) {
  24.         //外层循环，遍历次数
  25.         for (int j = 0; j < arr.length - i - 1; j++) {
  26.             //升序（如果前一个值比后一个值大，则交换）
  27.             if (arr[j] > arr[j + 1]) {
  28.                 flag = true;
  29.                 temp = arr[j + 1];
  30.                 arr[j + 1] = arr[j];
  31.                 arr[j] = temp;
  32.             }
  33.             if (!flag){
  34.                 break; //在一趟排序中，一次交换都没有发生过
  35.             }else {
  36.                 flag = false; //重置flag，进行下次判断
  37.             }
  38.         }
  39.     }
  40.     System.out.println(Arrays.toString(arr));
  41. }

2.2.2 选择排序

2.2.3 插入排序

2.2.4 希尔排序

2.2.5 归并排序

算法描述：
1) 归并排序是采用分治法的一个非常典型的应用。归并排序的思想就是先递归分解数组，再合并数组。
2) 将数组分解最小之后，然后合并两个有序数组
3) 基本思路是比较两个数组的最前面的数，谁小就先取谁，取了后相应的指针就往后移一位。
4) 然后再比较，直至一个数组为空，最后把另一个数组的剩余部分复制过来即可。

代码：

  1. public static void main(String[] args) {
  2.     int[] array = {2,1,4,3,5,1};
  3.     System.out.println(Arrays.toString(guibing(array)));
  4. }
  5. //归并排序  —— 一分为二，递归
  6. private static int[] guibing(int[] array) {
  7.     if (array.length <2)  return array;
  8.     int mid = array.length/2;
  9.     int[] left = Arrays.copyOfRange(array, 0, mid);
  10.     int[] right = Arrays.copyOfRange(array, mid, array.length);
  11.     return paixu(guibing(left), guibing(right));
  12. }
  13. //将两段排序好的数组合成一个排序好的数组
  14. private static int[] paixu(int[] left, int[] right) {
  15.     int[] result = new int[left.length+right.length];
  16.     for (int index = 0, i = 0, j = 0; index < result.length; index++) {
  17.         //表示左边的数字已经完全填进去了，到达左边数组末尾了，然后直接把右边的数组copy进来就好了，因为已经排序了
  18.         if (i>=left.length)
  19.             result[index] = right[j++];
  20.             //表示右边的数字已经完全填进去了，到达右边数组的末尾了，然后直接把左边的数组copy进来就好了
  21.         else if (j>=right.length)
  22.             result[index] = left[i++];
  23.             //如果左边的数大于右边的数，则把右边的数填进去，指针向后移
  24.         else if (left[i]>right[j])
  25.             result[index] = right[j++];
  26.             //如果右边的数大于左边的数，则把左边的数填进去，指针向后移
  27.         else
  28.             result[index] = left[i++];
  29.     }
  30.     return result;
  31. }

2.2.6 快速排序

算法描述：
1) 首先确定列表第一个数据为中间值，第一个值看成空缺（低指针空缺）。
2) 然后在剩下的队列中，看成有左右两个指针（高低）。
3) 开始高指针向左移动，如果遇到小于中间值的数据，则将这个数据赋值到低指针空缺，并且将高指针的数据看成空缺值（高指针空缺）。然后先向右移动一下低指针，并且切换低指针移动。
4) 当低指针移动到大于中间值的时候，赋值到高指针空缺的地方。然后先高指针向左移动，并且切换高指针移动。重复2)、3)操作。
5) 直到高指针和低指针相等时退出，并且将中间值赋值给对应相等指针位置。
6) 然后将中间值的左右两边看成行的列表，进行快速排序操作。

代码：

  1. //快排
  2. public static void main(String[] args) {
  3.     int arr[] = {7, 5, 3, 2, 4, 1, 8, 9, 6};
  4.     //快速排序
  5.     int low = 0;
  6.     int high = arr.length - 1;
  7.     quickSort(arr, low, high);
  8.     System.out.println(Arrays.toString(arr));
  9. }
  10. public static void quickSort(int[] arr, int low, int high) {
  11.     //如果指针在同一位置(只有一个数据时)，退出
  12.     if (high - low < 1) {
  13.         return;
  14.     }
  15.     //标记，从高指针开始，还是低指针（默认高指针）
  16.     boolean flag = true;
  17.     //记录指针的其实位置
  18.     int start = low;
  19.     int end = high;
  20.     //默认中间值为低指针的第一个值
  21.     int midValue = arr[low];
  22.     while (true) {
  23.         //高指针移动
  24.         if (flag) {
  25.             //如果列表右方的数据大于中间值，则向左移动
  26.             if (arr[high] > midValue) {
  27.                 high--;
  28.             } else if (arr[high] < midValue) {
  29.                //如果小于，则覆盖最开始的低指针值，并且移动低指针，标志位改成从低指针开始移动
  30.                 arr[low] = arr[high];
  31.                 low++;
  32.                 flag = false;
  33.             }
  34.         } else {
  35.             //如果低指针数据小于中间值，则低指针向右移动
  36.             if (arr[low] < midValue) {
  37.                 low++;
  38.             } else if (arr[low] > midValue) {
  39.      //如果低指针的值大于中间值，则覆盖高指针停留时的数据，并向左移动高指针。切换为高指针移动
  40.                 arr[high] = arr[low];
  41.                 high--;
  42.                 flag = true;
  43.             }
  44.         }
  45.         //当两个指针的位置相同时，则找到了中间值的位置，并退出循环
  46.         if (low == high) {
  47.             arr[low] = midValue;
  48.             break;
  49.         }
  50.     }
  51.     //然后出现有，中间值左边的小于中间值。右边的大于中间值。
  52.     //然后在对左右两边的列表在进行快速排序
  53.     quickSort(arr, start, low -1);
  54.     quickSort(arr, low + 1, end);
  55. }
  62. // 左程云解法：
  63. public static void main(String[] args) {
  64.     int[] arr = new int[]{6, 2, 3, 4, 5, 6};
  65.     quickSort(arr);
  66.     System.out.println(Arrays.toString(arr));
  67. }
  69. private static void quickSort(int[] arr) {
  70.     if (arr == null || arr.length < 2) {
  71.         return;
  72.     }
  73.     quickSort(arr, 0, arr.length - 1);
  74. }
  76. private static void quickSort(int[] arr, int l, int r) {
  77.     if (l < r) {
  78.         swap(arr, l + (int) (Math.random() * (r - l + 1)), r);
  79.         int[] p = partition(arr, l, r);  // 存储中间值的左右边界
  80.         quickSort(arr, l, p[0] - 1);
  81.         quickSort(arr, p[1] + 1, r);
  82.     }
  83. }
  85. // 左边界  中间 右边界
  86. private static int[] partition(int[] arr, int l, int r) {
  87.     int less = l - 1;  // <区右边界
  88.     int more = r;// >区左边界
  89.     while (l < more) {
  90.         if (arr[l] < arr[r]) {
  91.             swap(arr, ++less, l++);
  92.         } else if (arr[l] > arr[r]) {
  93.             swap(arr, --more, l);
  94.         } else {
  95.             l++;
  96.         }
  97.     }
  98.     swap(arr, more, r);
  99.     return new int[]{less + 1, more};
  100. }
  102. public static void swap(int[] arr, int a, int b) {
  103.     //        arr[a] = arr[a] ^ arr[b];
  104.     //        arr[b] = arr[a] ^ arr[b];
  105.     //        arr[a] = arr[a] ^ arr[b];
  106.     int temp;
  107.     temp = arr[a];
  108.     arr[a] = arr[b];
  109.     arr[b] = temp;
  110. }


https://www.cnblogs.com/ll409546297/p/10956960.html