题目

我们有一个由平面上的点组成的列表 points。需要从中找出 K 个距离原点 (0, 0) 最近的点。平面上两点之间的距离是欧几里德距离。

示例

  1. (转自leetcode)
  2. 输入：points = [[1,3],[-2,2]], K = 1
  3. 输出：[[-2,2]]
  4. 解释： 
  5. (1, 3) 和原点之间的距离为 sqrt(10)，
  6. (-2, 2) 和原点之间的距离为 sqrt(8)，
  7. 由于 sqrt(8) < sqrt(10)，(-2, 2) 离原点更近。
  8. 我们只需要距离原点最近的 K = 1 个点，所以答案就是 [[-2,2]]
  10. 来源：力扣（LeetCode）
  11. 链接：https://leetcode-cn.com/problems/k-closest-points-to-origin
  12. 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

提示

  • 初中数学中的直角斜边的公式(a平方 + b平方 = c平方)
  • js内置一个API,(Math.hypot(a, b) = c).方法返回所有参数的平方和的平方根

    所以

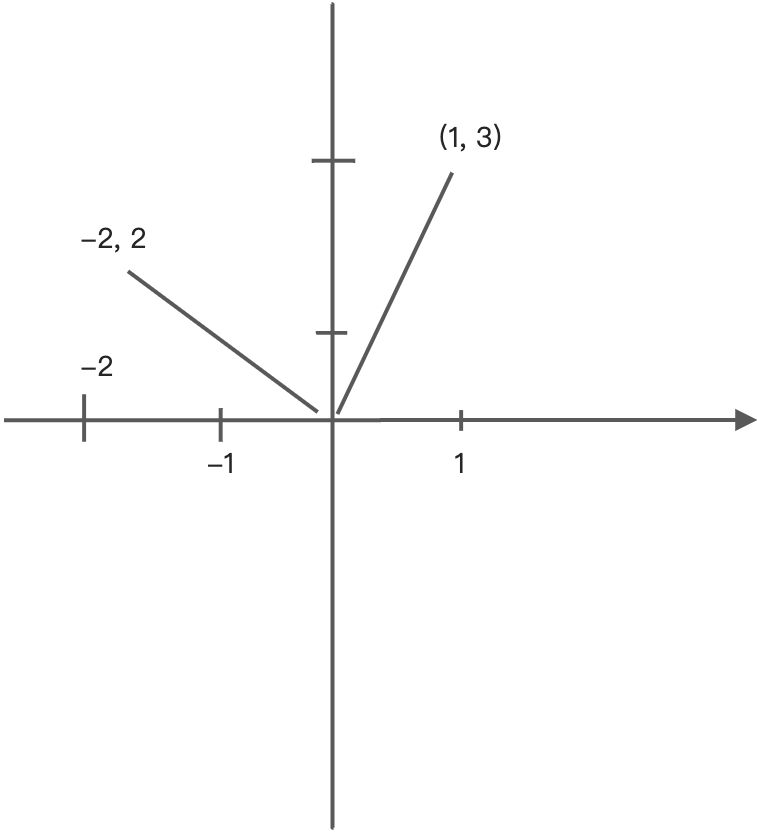
    最接近原点的 K 个点(leetcode) - 图1
    求的就是上图中的两条斜线 ```javascript 斜线 (-2, 2)到原点设为c1 斜线 (1, 3)到原点设为c2

c1 = Math.sqrt(Math.pow(-2, 2) + Math.pow(-2, 2), 2); c2 = Math.sqrt(Math.pow(1, 2) + Math.pow(3, 2), 2);

// Math.hypot来表示就是, 简便了很多 c1 = Math.hypot(-2, 2); c2 = Math.hypot(1, 3);

  1. <a name="c7nTU"></a>
  2. ### 实现
  4. - 使用大顶堆来写
  5. ```javascript
  6. /**
  7.  * @param {number[][]} points
  8.  * @param {number} k
  9.  * @return {number[][]}
  10.  */
  11. var kClosest = function(points, k) {
  12.     const distanceMap = transform(points);
  13.     const heap = [];
  14.     distanceMap.forEach((item) => {
  15.         if (heap.length < k) {
  16.             push(heap, item);
  17.         } else {
  18.             if (heap[0].distance > item.distance) {
  19.                 pop(heap);
  20.                 push(heap, item);
  21.             }
  22.         }
  23.     });
  24.     return heap.map((item) => points[item.key]);
  25. };
  27. /**
  28.  * 将计算出点于原点的距离
  29.  */
  30. function transform(points) {
  31.     return points.map((point, index) => {
  32.         return {
  33.             key: index,
  34.             distance: Math.hypot(point[0], point[1]),
  35.         };
  36.     });
  37. };
  39. // 大顶堆
  40. // 将距离最远的放入堆顶
  41. // 当堆内达到指定的数量后,比较堆顶于当前推入元素大小
  43. function pop(heap) {
  44.     if (heap.length === 0) {
  45.         return;
  46.     }
  47.     const first = heap[0];
  48.     const last = heap.pop();
  50.     if (first !== last) {
  51.         heap[0] = last;
  52.         siftDown(heap, last, 0);
  53.     }
  54.     return first;
  55. }
  57. function push(heap, node) {
  58.     const len = heap.length;
  59.     heap.push(node);
  60.     siftUp(heap, node, len);
  61. }
  63. function compare(a, b) {
  64.     return a.distance - b.distance;
  65. };
  67. function siftUp(
  68.     heap,
  69.     node,
  70.     i,
  71. ) {
  72.     let index = i;
  73.     while(index > 0) {
  74.         const parentIndex = (index - 1) >>> 1;
  75.         const parent = heap[parentIndex];
  76.         if (compare(node, parent) > 0) {
  77.             heap[parentIndex] = node;
  78.             heap[index] = parent;
  79.             index = parentIndex;
  80.         } else {
  81.             return;
  82.         }
  83.     }
  84. };
  86. function siftDown(
  87.     heap,
  88.     node,
  89.     i,
  90. ) {
  91.     const length = heap.length;
  92.     const halfIndex = length >>> 1;
  93.     let parentIndex = i;
  94.     while(parentIndex < halfIndex) {
  95.         const leftIndex = (parentIndex << 1) + 1;
  96.         const left = heap[leftIndex];
  97.         const rightIndex = leftIndex + 1;
  98.         const right = heap[rightIndex];
  99.         if (compare(left, node) > 0) {
  100.             if (rightIndex < length && compare(right, left) > 0) {
  101.                 heap[rightIndex] = node;
  102.                 heap[parentIndex] = right;
  103.                 parentIndex = rightIndex;
  104.             } else {
  105.                 heap[leftIndex] = node;
  106.                 heap[parentIndex] = left;
  107.                 parentIndex = leftIndex;
  108.             }
  109.         } else if (rightIndex < length && compare(right, node) > 0) {
  110.             heap[rightIndex] = node;
  111.             heap[parentIndex] = right;
  112.             parentIndex = rightIndex;
  113.         } else {
  114.             return;
  115.         }
  116.     }
  117. };