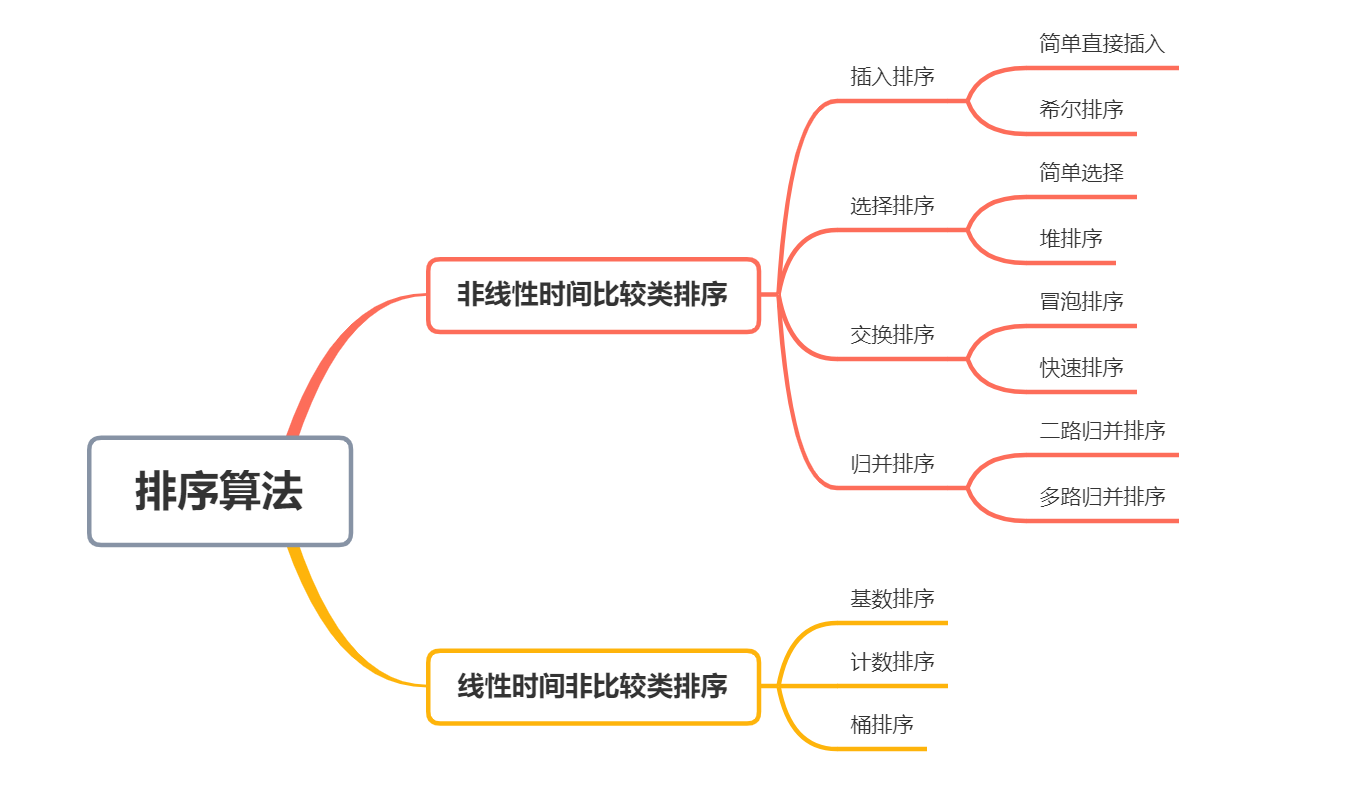
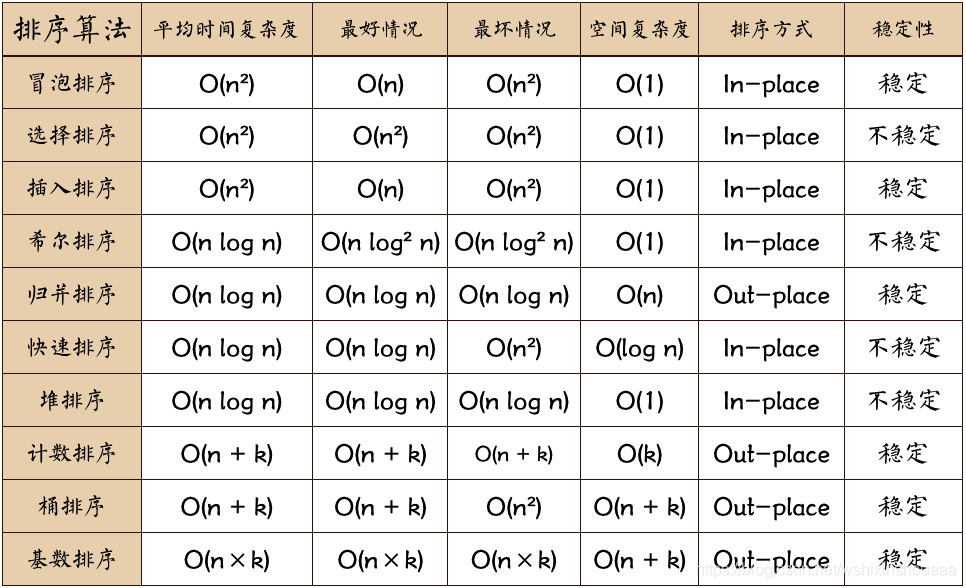
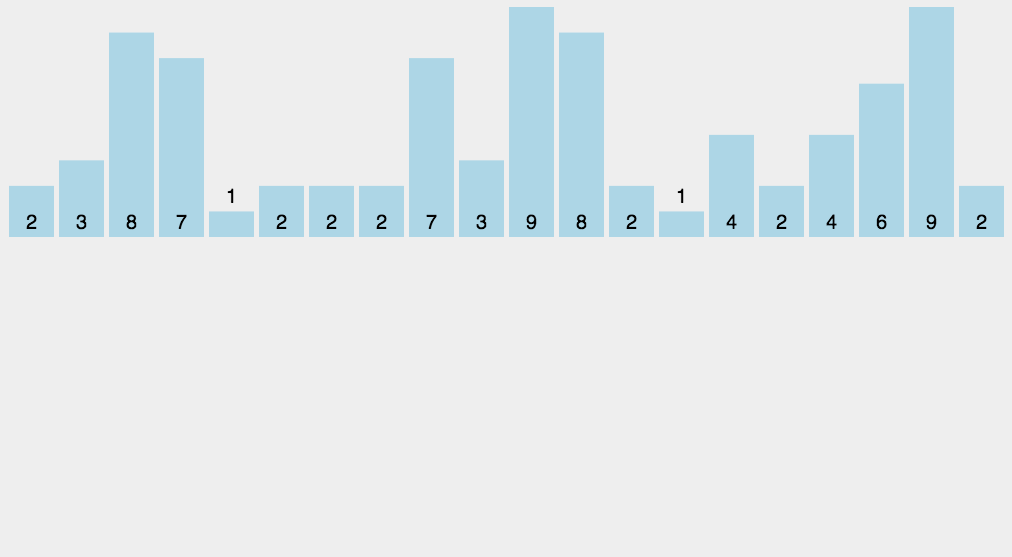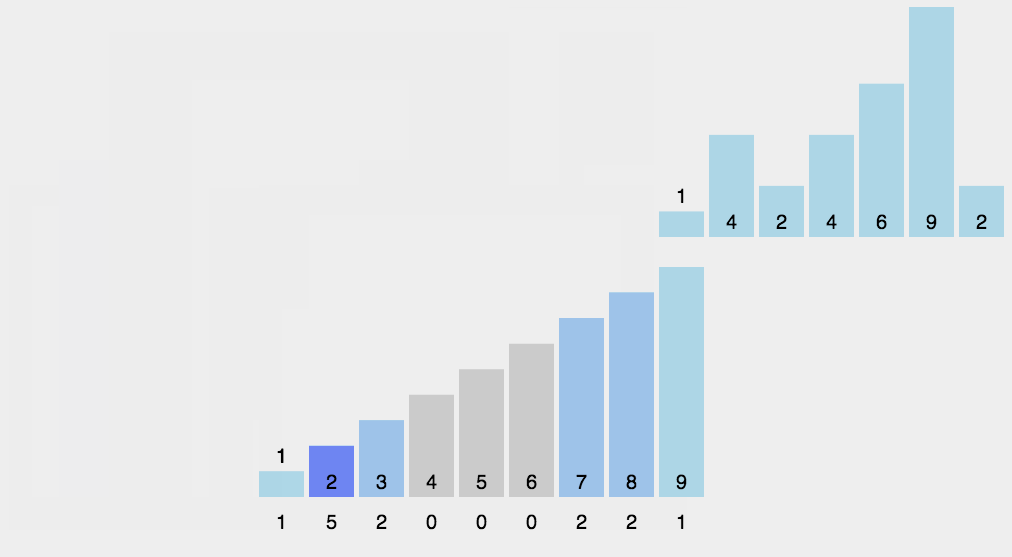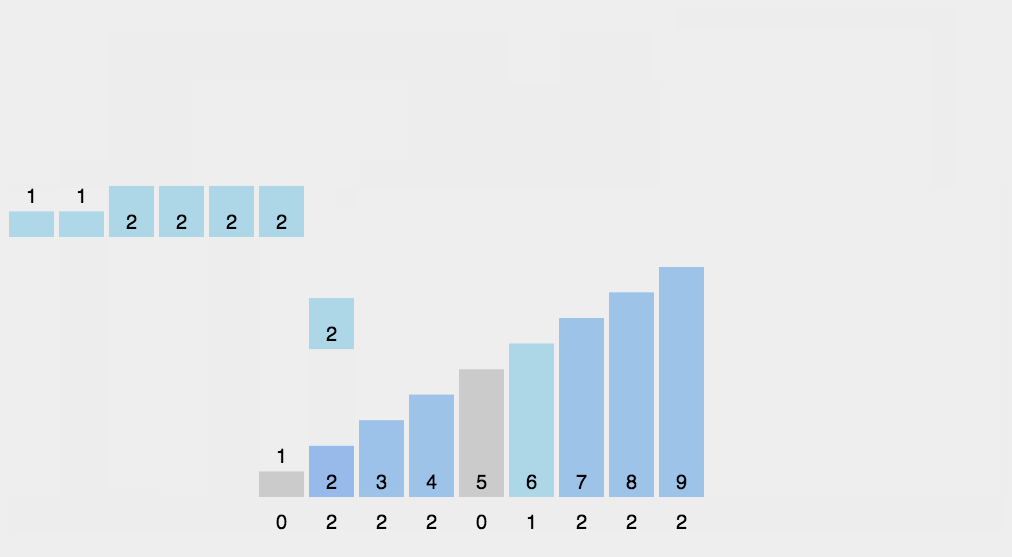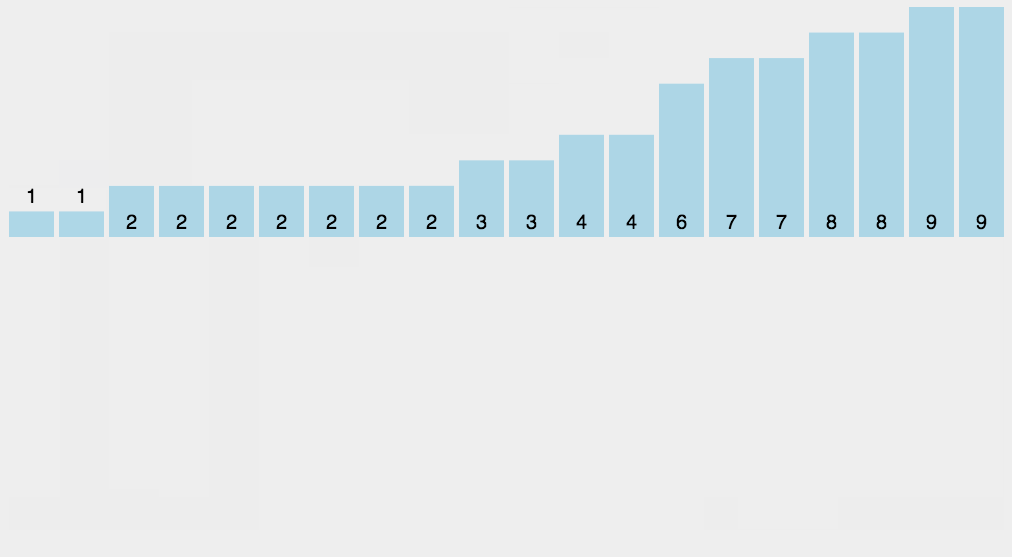基础算法--十大排序算法

结构
性质
插入排序
- 简单直接插入
- 希尔排序（递减增量排序）
选择排序
- 简单选择排序
- 快速排序
交换排序
- 冒泡排序
- 堆排序
归并排序(外排序)
- 二路归并
- 多路归并
其他排序

结构

性质

基础算法--十大排序算法 - 图2

稳定性

相同值排序状态前后相对位置不变
稳定的
- 冒泡
- 插入（有时很吊）
- 归并（递归空间O(n)）
- 桶（不基于比较的）
- 计数（非比较、局限）
- 基数（非比较、局限）
不稳定的
- 选择（垃）
- 希尔（选择）（一般很吊）
- 快速
- 堆
目前没有时间O(nlogn)空间O(1) 又稳定的排序

重要的：
选择（最垃）、插入、冒泡、归并（递归、稳定、空间高）、快速（最快、不稳、空间中等）、桶。

牛逼的：
快排（快，空间O(nlogn)，不稳定）
归并（稳定性，时间O(nlog)）

插入排序

简单直接插入
简介
- 从第一个元素开始，认为该元素是已经排序的
- 去下一元素，与之前排序过的部分比较
- 比前面小，插入并将已排序部分大的后移一位。
- 大，将该元素移到下一位值。
- 遍历直至结束。
- 联想：牌。
性能
- 时间平均O(n2)。
- 空间O(1)
演示

基础算法--十大排序算法 - 图3

代码 ```java import java.util.Arrays;

/**

@author Skiray
@Program:shuti
@date 2021/7/19 8:38

插入排序—简单插入排序 */ public class InsertSort { // 通过全交换排序 public static void main(String[] args) {

 int[] arr = {8, 1, 4, 9, 3, 5, 2, 7, 0, 6};
 System.out.println(Arrays.toString(arr));
 insertSort(arr);
 System.out.println(Arrays.toString(arr));

} private static void insertSort(int[] a){

 for (int i = 0; i < a.length - 1 ; i++) {
     int data = a[i+1]; //要调整的值，一次循环中，data不变，结束时找到合适位置放入。
     int index = i;
     while (index >= 0 && a[index] >data){
         a[index + 1] = a[index]; //后移，产生重复值。data保存被覆盖值。
         index--; //游标
     }
     a[index + 1] = data;  //data放到指定位置。
 }

} } ```

希尔排序（递减增量排序）

性能
- 时间：O(nlogn)
- 空间：O(1)
思想
- 按照步长进行分组，将每组元素利用直接插入排序；
- 每次将步长折半，循环；
- 当步长为1利用直接插入完成排序。
描述
- 选择一个增量序列t1,t2…,tk，其中ti > tj，tk = 1;
- 按增量序列个数k，堆序列进行k躺排序
- 每趟排序，根据对应的增量ti，将待排序序列分割成若干长度为m的子序列，分别堆各子表进行直接插入排序。仅增量因子为1时，整个序列作为一个表来处理，表长度即为整个序列的长度。
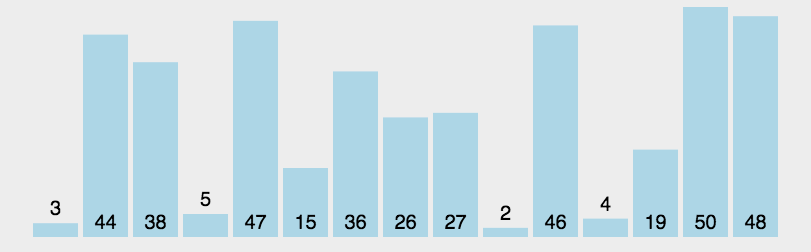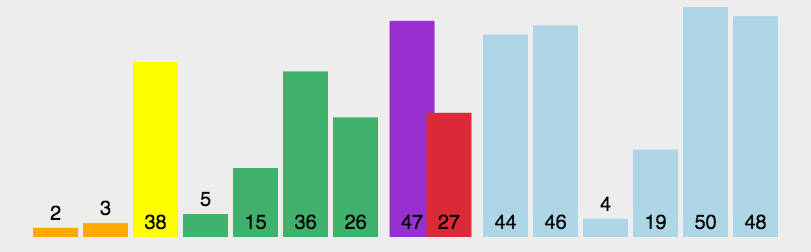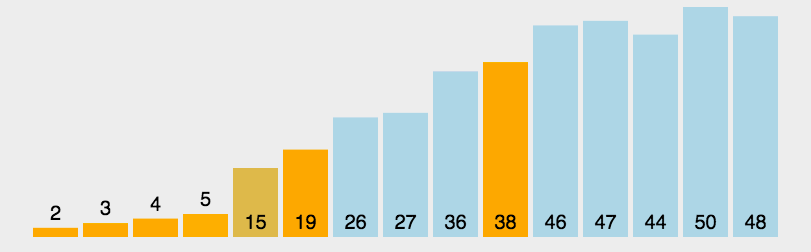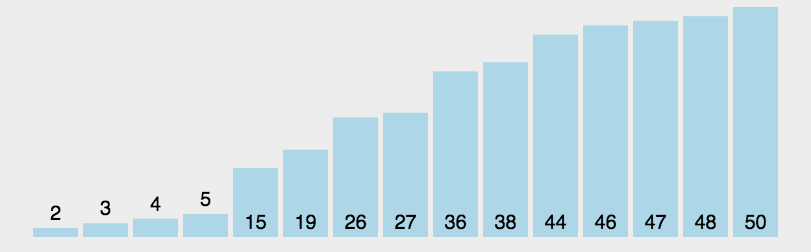
演示

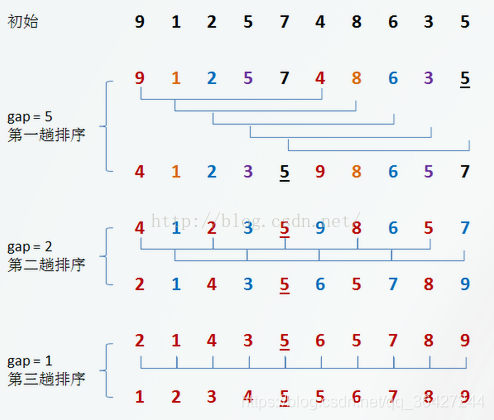
基础算法--十大排序算法 - 图4

代码 ```java import java.util.Arrays;

/**

@author Skiray
@Program:shuti
@date 2021/7/19 8:50

插入排序—希尔排序 */ public class ShellSort { public static void main(String[] args) {

 int[] arr = {8, 1, 4, 9, 3, 5, 2, 7, 0, 6};
 System.out.println(Arrays.toString(arr));
 shellSort(arr);

} private static void shellSort(int[] array){

 int gap = array.length >> 1;  //分为 length/gap 组
 while (gap > 0){
     for (int i = gap; i < array.length ; i++) {
         int index = i-gap;
         int temp = array[i];
         while (index >= 0 && array[index] > temp){
             swap(array,index,index + gap);
             index -= gap;
         }

// array[index + gap] = temp;

     }
     gap >>= 1;
     System.out.println(Arrays.toString(array));
 }

} private static void swap(int[] array, int i,int index){

 int temp = array[i];
 array[i] = array[index];
 array[index] = temp;

} } ```

选择排序

简单选择排序

描述
- 从未排序的初始数组中寻找最小元素放置首位。
- 从剩余元素中继续寻找最小元素，放到已排序序列的尾部。
- 遍历数组，直至结束。
性能
- 时间O(n2);
- 空间O(1)
演示

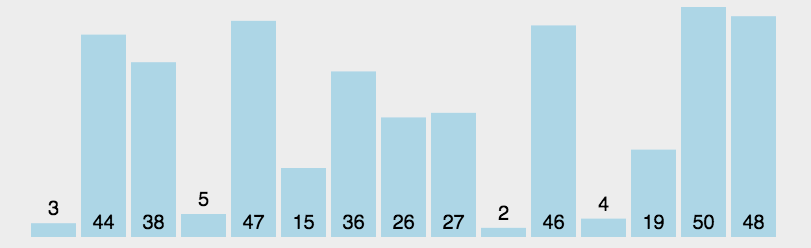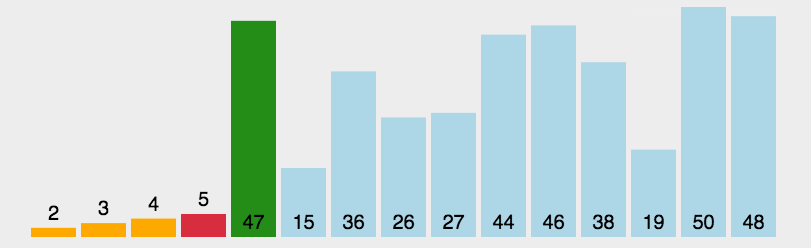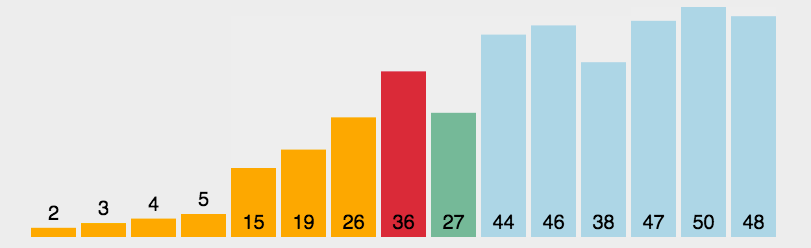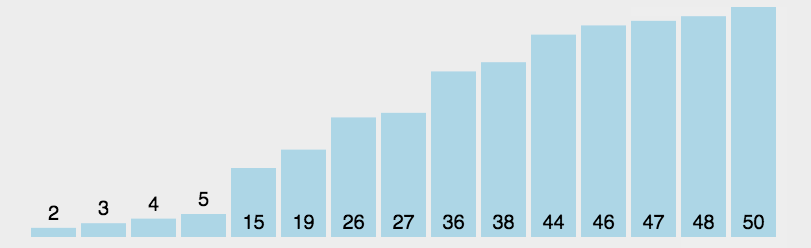
基础算法--十大排序算法 - 图5

代码 ```java import java.util.Arrays;

/**

@author Skiray
@Program:shuti
@date 2021/7/19 9:04

选择排序—简单选择 */ public class SelectSort { public static void main(String[] args) {

 int[] arr = {8, 1, 4, 9, 3, 5, 2, 7, 0, 6};
 System.out.println(Arrays.toString(arr));
 selectSort(arr);
 System.out.println(Arrays.toString(arr));

} private static void selectSort(int[] array){

 for (int i = 0; i < array.length; i++) {
     int index = i;
     for (int j = i; j < array.length; j++) {//未排序部分
         if (array[j] < array[index]){
             index = j; //未排序中最小的位置索引
         }
     }
     swap(array,index,i); //将挑选的最小元素与已经排序末尾交换。
 }

} private static void swap(int[] array,int index,int i){

 int temp = array[index];
 array[index] = array[i];
 array[i] = temp;

} } ```

快速排序

思想
- 挖坑填数 + 分治法
- 使用分治法策略来吧一个串行（list）分为两个字串行（list sub）
- 是一种分而治之思想再排序算法上的典型应用。本质上，快排是冒泡基础上的递归分治法。
性能
- 时间O(nlogn);
描述
- 从数列中挑出一个元素，称为基准。
- 重新排序数列，所有比基准值小的元素摆放在基准前面，所有比基准值大的元素摆在基准后面（相同可任意）。在这个分区结束后，该基准就处于数列的中建位置。这个称为分区（pacrition）操作。
- 递归地(recursively)把小于基准值元素的子数列和大于基准元素的子数列排序。
演示
代码 ```java import java.util.Arrays;

/**

@author Skiray
@Program:shuti
@date 2021/7/19 11:00

选择排序—快速排序 */ public class QuickSort { public static void main(String[] args) {

 int[] array = {8, 1, 4, 9, 3, 5, 2, 7, 0, 6};
 System.out.println(Arrays.toString(array));
 sort(array,0, array.length - 1);
 System.out.println(Arrays.toString(array));

} public static int selectPivot(int[] array,int left,int right){

 int middle = (left + right) / 2;
 if (array[middle] > array[right])
     swap(array,middle,left);
 if (array[left] > array[right])
     swap(array,left,left);
 if (array[middle] > array[left])
     swap(array,left,middle);
 return array[left];

} public static void sort(int[] array,int left,int right){

 if (left >= right) return;
 int index = partition(array,left,right);
 sort(array, left, index - 1 );
 sort(array, index + 1, right);

} public static int partition(int[] array,int left, int right){

 int pivot = selectPivot(array, left, right);
 while (left < right){
     while (left < right && array[right] >= pivot){
         right--;
     }
     if (left < right){
         array[left++] = array[right];
     }
     while (left < right && array[left] < pivot){
         left++;
     }
     if (left < right){
         array[right--] = array[left];
     }
 }
 array[right] = pivot;
 return right;

} public static void swap(int[] array,int left,int right){

 int value = array[left];
 array[left] = array[right];
 array[right] = value;

} } ```

交换排序

冒泡排序

描述
- 一次比较相邻的两个元素，若前者比后者大则交换，这样数组的最后一位是最大值。
- 在除了最后一位的未排序数组上继续重复以上步骤，每一步都能找到一个最大值放在后面。
- 遍历数组，直至结束。
性能
- 时间最好（已排序）O(n2)，平均O(n2)。
演示
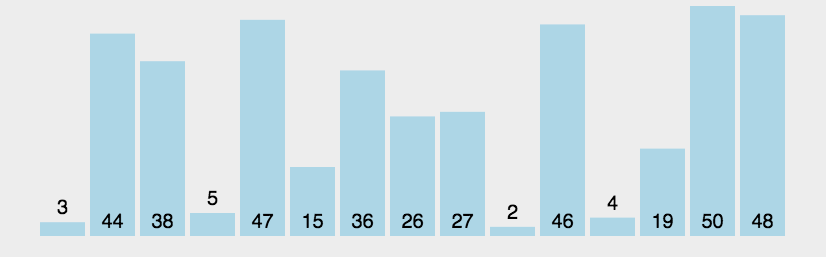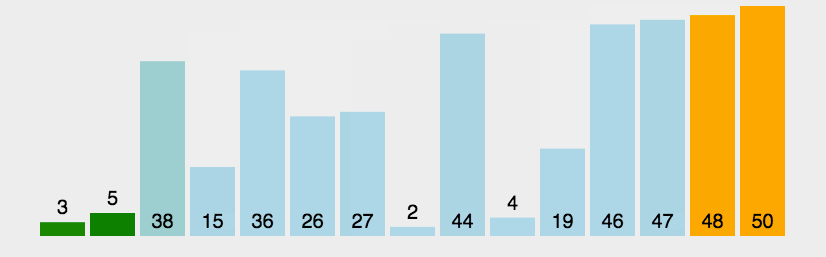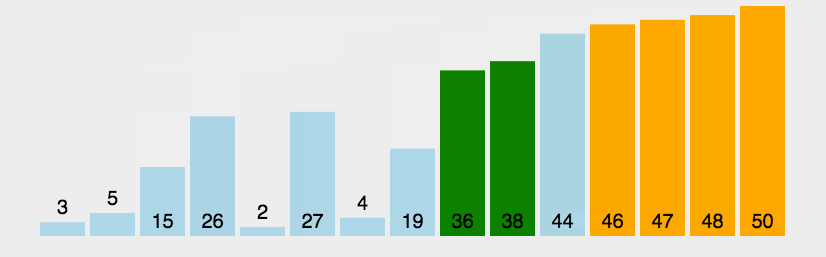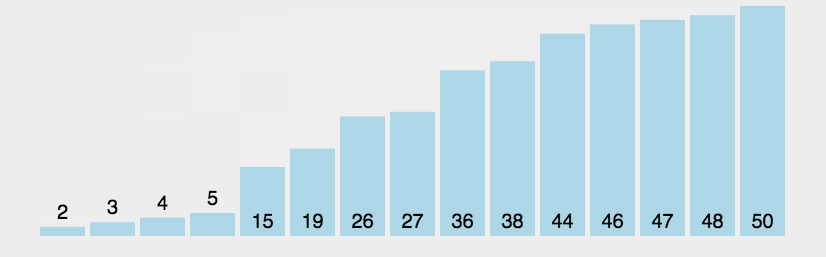
代码 ```java import java.util.Arrays;

/**

@author : Skiray
@Program :shuti
@date : 2021/7/19 10:33

交换排序—冒泡排序 */ public class BubbleSort { public static void main(String[] args) {

 int[] nums = { 6, 3, 8, 2, 9, 1 };
 System.out.println(Arrays.toString(nums));
 bubbleSort(nums);
 System.out.println(Arrays.toString(nums));

} private static void bubbleSort(int[] nums){

 for (int i = 0; i < nums.length - 1 ; i++) {
     for (int j = 0; j < nums.length -1 - i; j++) {
         if (nums[j] > nums[j + 1]){
             swap(nums,j,j + 1);
         }
         System.out.println(Arrays.toString(nums));
     }
 }

} private static void swap(int[] nums,int j, int i){

 int temp = nums[j];
 nums[j] = nums[i];
 nums[i] = temp;

} } ```

堆排序

思想
- 已知堆的定义
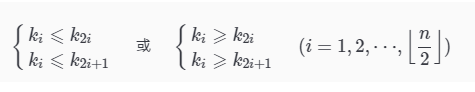
- 把此序列对应的二维数组看成一个完全二叉树，那么堆的含义就是：完全二叉树中任一个非叶子节点的值均不大于（或不小于）其左，右孩子节点的值。
- 由以上可知大顶堆的堆顶的关键字肯定是所有关键字中最大的，小顶堆的堆顶的关键字是所有关键字中最小的。
- 因此我们可使用大顶堆进行升序排序，使用小顶堆进行降序排序。
以大顶堆为例，堆排序的过程就是将排序的序列构造成一个堆，选出堆中最大的移走，再把剩余的元素调整成堆，找出最大的再移走，重复直至有序。
描述
- 先将初始序列K[1…n]K[1…n]建成一个大顶堆，那么此时第一个元素K1K1最大，此堆为初始的无序区。
- 再将关键字最大的记录K1K1(即堆顶，第一个元素)和无序区的最后一个记录KnKn交换，由此得到新的无序区K[1…n-1]K[1…n-1]和有序去K[n]K[n]，且满足K[1…n−1].keys⩽K[n].keyK[1…n−1].keys⩽K[n].key
- 交换K1K1和KnKn后，堆顶可能违反堆性质，因此需将K[1…n-1]K[1…n-1]调整为堆，然后重复步骤2，直至无序区只有一个元素时停止。
性能
- 时间O(nlogn);

基础算法--十大排序算法 - 图9

代码 ```java import java.util.Arrays;

/**

@author Skiray
@Program:shuti
@date 2021/7/19 9:20
交换排序—堆排序 */ public class HeapSort { public static void main(String[] args) {
```
 int[] array = { 15, 13, 12, 5, 20, 1, 8, 9 };
 System.out.println(Arrays.toString(array));
 creatHeap(array, array.length - 1);
 System.out.println(Arrays.toString(array));
```
// deleteHeap(array, array.length - 1); // System.out.println(Arrays.toString(array)); // deleteHeap(array, array.length - 2); // System.out.println(Arrays.toString(array)); // insertHeap(array, 3,array.length - 2); // System.out.println(Arrays.toString(array)); } // 建堆 public static void creatHeap(int[] arr,int n){ // 数组从0开始
```
 for (int i = (n-1) >> 1; i >= 0 ; i--) {
     percolateDown(arr,i,n);
 }
```
} // 插入 private static void insertHeap(int[] array,int data,int n){
```
 array[n] = data;
 percolatrUp(array,n);
```
} // 删除栈顶元素 public static void deleteHeap(int[] arr,int n) {
```
 arr[0] = arr[n];
 arr[n] = -1;
 percolateDown(arr,0,n-1);
```
} // 上浮 private static void percolatrUp(int[] array,int n){
```
 int data = array[n];
 int father = (n-1)>>1;
 while (data < array[father] && father >= 0){
     array[n] = array[father];
     array[father] = data;
     n = father;
```
// father = (n-1) >> 1;
```
     father = (n-1) / 2; //负数不用轻易使用位运算
 }
 array[father] = data;
```
} // 下滤 private static void percolateDown(int[] arr,int i, int n){
```
 int father = arr[i];
 int child = 2 * i + 1;
```
// 遍历整个该节点的子树
```
 while (child <= n){
```
// 定位左右节点小的那一个
```
     if (child + 1 <= n && arr[child + 1] < arr[child]){
         child +=1;
     }
```
// 若根节点比子节点小，说明已经是一个小堆
```
     if (father < arr[child]){
         break;
     }
```
// 互换跟节点和子节点
```
     arr[i] = arr[child];
     arr[child] = father;
```
// 重新定位根节点和子节点
```
     i = child;
     child = i * 2 + 1;
 }
```
} } ```
归并排序(外排序)

思想
- 将两个（或以上）有序表合并成一个新的有序表，即把待排序序列分为若干子序列，每个序列是有序的，然后再把有序序列合并为整体有序序列。
描述
- 将长序列从中间分成两个子序列。
- 堆两个子序依次继续执行重复分裂，直至不能再分。
- 归并返回两两排好序的子序列。
实现
- 自上而下的递归
  - 将序列每相邻数字进行归并操作，形成floor(n/2)个序列，排序后每个序列包含两个元素
  - 将上述序列再次归并，形成floor(n/4)个序列，每个序列包含四个元素
  - 重复2步骤，直至完成。
- 自下而上的迭代
  - 申请空间，是其大小为两个已经排序序列之和，该空间用来存放合并后的序列
  - 设定两个指针，最初位置分别为两个已经排序序列的起始位置。
  - 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一个位置
  - 重复3步骤直至某指针到达序列末尾
  - 将另一序列剩下的所有元素直接赋值到合并序列尾部。
性能
- 时间：O(nlogn).
- 空间：O(n)
演示
- 二路归并
代码 ```java import java.util.Arrays;

/**

@author Skiray
@Program:shuti
@date 2021/7/19 14:11

归并排序—二路归并 */ public class mergeSort { public static void main(String[] args) {

 int[] array = {8, 9, 1, 7, 2, 3, 5, 4, 6, 0};
 int[] arr = MergeSort(array);
 System.out.println(Arrays.toString(arr));

} private static int[] MergeSort(int[] array){

 if (array.length < 2){
     return array;
 }
 int middle = array.length >> 1;
 int[] leftArray = Arrays.copyOfRange(array,0,middle);
 int[] rightArray = Arrays.copyOfRange(array,middle,array.length);
 return merge(MergeSort(leftArray),MergeSort(rightArray));

} private static int[] merge(int[] leftArray, int[] rightArray) {

 int[] result = new int[leftArray.length + rightArray.length];
 for (int index = 0, i = 0, j = 0; index < result.length; index++) {
     if (i >= leftArray.length){
         result[index] = rightArray[j++];
     }else if (j >= rightArray.length){
         result[index] = leftArray[i++];
     }else if (leftArray[i] > rightArray[j]){
         result[index] = rightArray[j++];
     }else {
         result[index] = leftArray[i++];
     }
 }
 return result;

} } ```

多路归并

其他排序

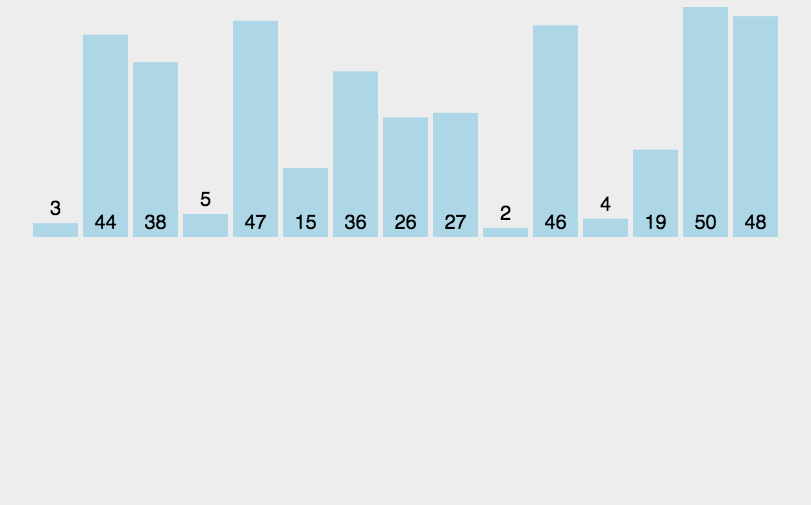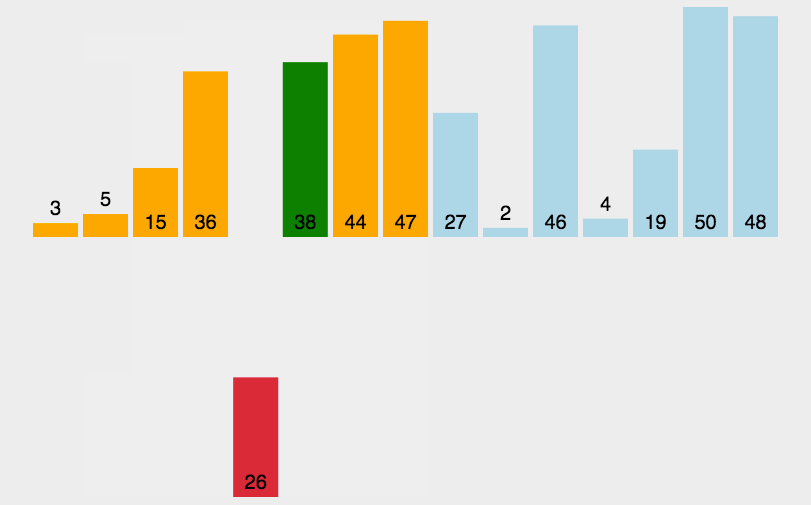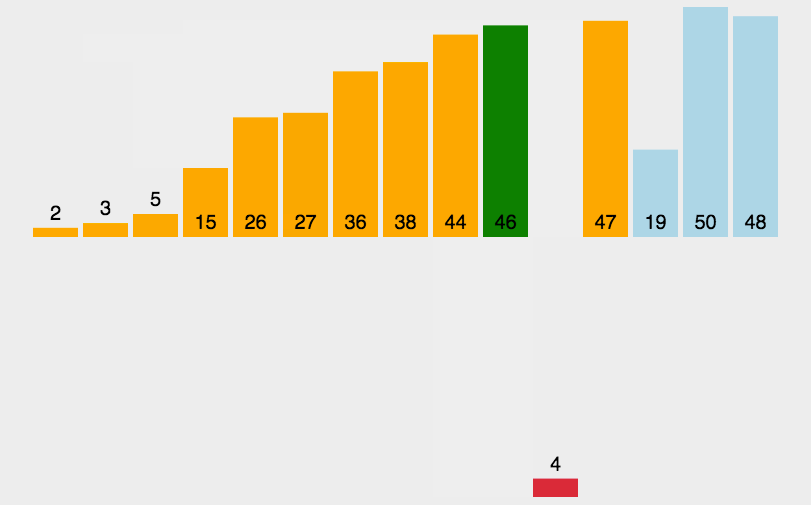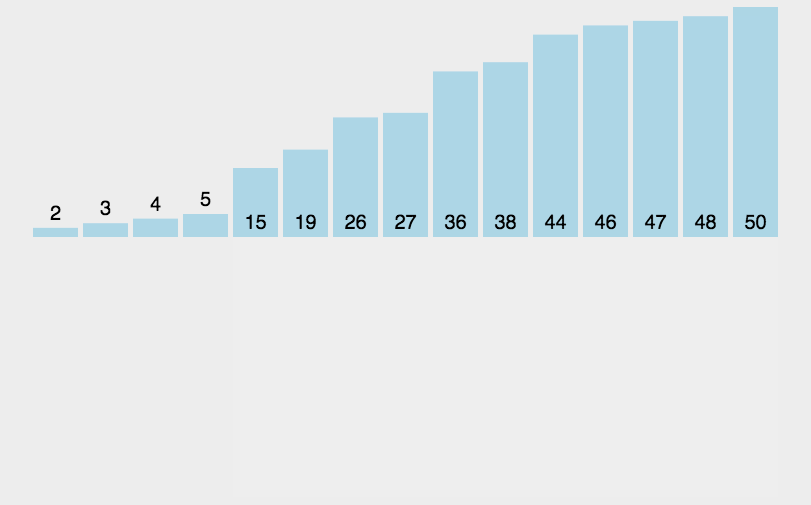
基数排序

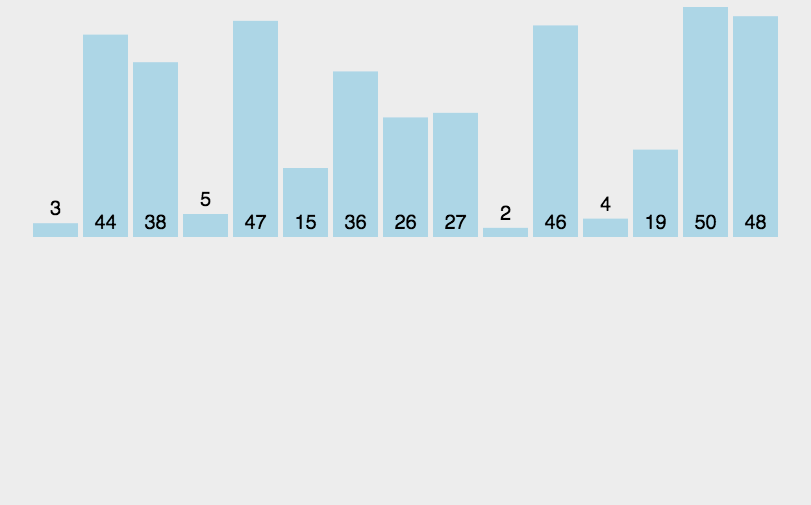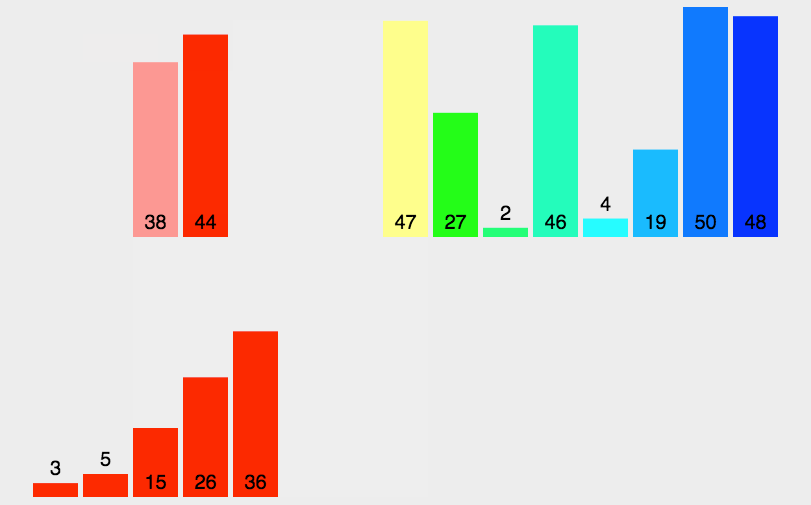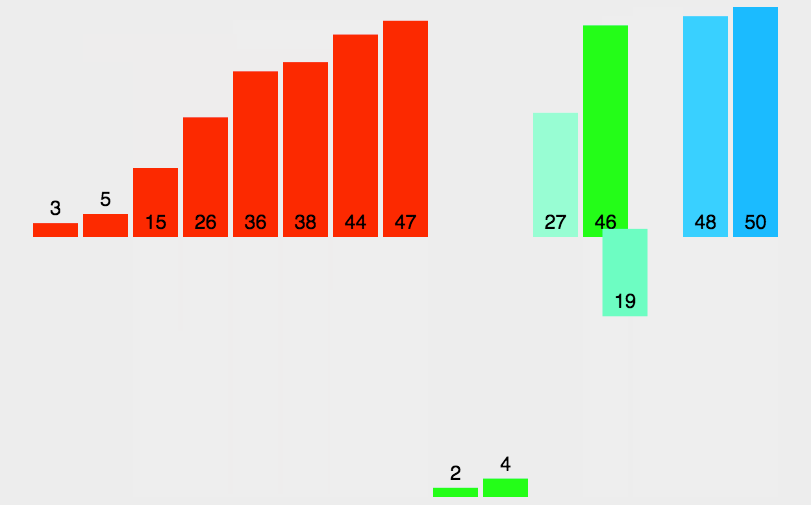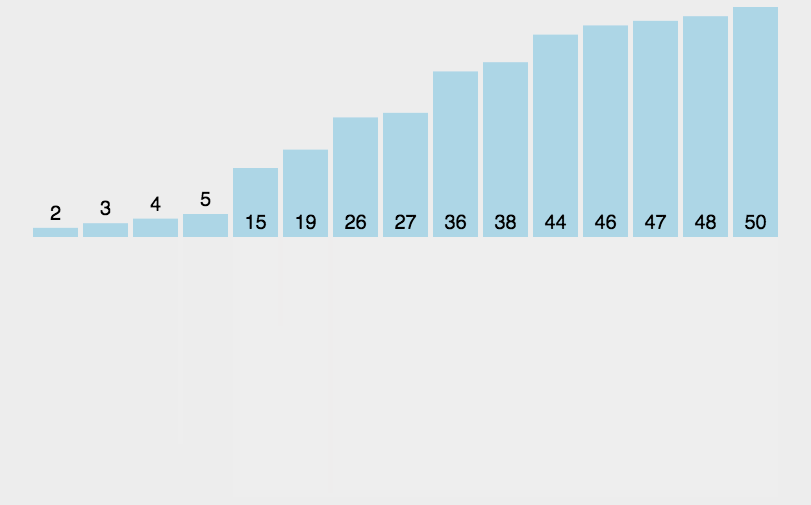
描述
- 找到数组中最大的数，确定最多一共有几位数。
- 按照每个数字的最后一位，放入辅助数组中；同时设置一个计数数组，统计以数字i结尾的数字个数。
- 将辅助数组中的元素重新放入原数组中，然后按照下一位继续重复以上动作。
性能
- 时间O(n*k).
演示
代码 ```java import java.util.Arrays;

/**

@author Skiray
@Program:shuti
@date 2021/7/19 14:21

其他排序—基数排序 */ //待debug public class RadixSort { public static void main(String[] args) {

 int[] array = {3, 44, 38, 4, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 32};
 int[] arr = radixSort(array);
 System.out.println(Arrays.toString(arr));

} private static int[] radixSort(int[] array) {

 if (array == null || array.length < 2){
     return array;
 }

// 根据最大值找到最大位数

 int max = 0;
 for (int i = 0; i < array.length; i++) {
     max = Math.max(max,array[i]);
 }
 int maxDigit = 0;
 while (max != 0){
     max /= 10;
     maxDigit++;
 }

// 第一维: 0~9

 int[][] radix = new int[10][array.length];

// 该位为 i 的元素个数

 int[] count = new int[10];
 int m = 1;
 int n = 1;
 while (m <= maxDigit){
     for (int i = 0; i < array.length; i++) {
         int lsd = (array[i] / n) % 10;
         radix[lsd][count[lsd]] = array[i];
         count[lsd]++;
     }
     for (int i = 0, k = 0; i < 10; i++) {
         if (count[i] != 0){
             for (int j = 0; j < count[i]; j++) {
                 array[k++] = radix[i][j];
             }
         }
         count[i] = 0;
     }
     m *= 10;
     m++;
 }
 return array;

} } ```

计数排序

描述
- 找到数组中最小值和最大值，辅助数组的大小为两者之差。设置最小2，最大9，则辅助数组大小为7。
- 统计数组中每个元素出现的次数，减去最小值，存入辅助数组中。比如2，存放在辅助数组的第0位，7放在辅助数组的第5位。
- 最后反向填充数组。遍历原数组，依次将辅助数组不为0的元素下标加最小值，放回原数组对应位置。
性能
- 时间O(n+k).
演示
代码
```java import java.util.Arrays;

/**

@author Skiray
@Program:shuti
@date 2021/7/19 14:35

其他排序—计数排序 */ public class CountSort { public static void main(String[] args) {

 int[] array = {8, 9, 4, 7, 2, 3, 5, 4, 6, 8};
 int[] arr = countSort(array);
 System.out.println(Arrays.toString(arr));

} private static int[] countSort(int[] array) {

 if (array.length == 0) return array;
 int min = array[0], max = array[0];
 for (int i = 0; i < array.length; i++) {
     if (min > array[i])
         min = array[i];
     if (max < array[i])
         max = array[i];
 }
 int[] count = new int[max - min + 1];
 for (int i = 0; i < array.length; i++) {
     count[array[i] - min]++;
 }
 int i = 0;
 int index = 0;
 while (index < array.length){
     if (count[0] != 0){
         array[index] = i + min;
         count[i]--;
         index++;
     } else {i++;}
 }
 return array;

} } ```

结构

性质

稳定性

重要的：

牛逼的：

插入排序

简单直接插入

希尔排序（递减增量排序）

选择排序

简单选择排序

快速排序

交换排序

冒泡排序

堆排序

归并排序(外排序)

二路归并

多路归并

其他排序

基数排序

计数排序

桶排序