1.强化学习的概念

强化学习是机器学习的一个领域，它是关于采取适当的行动，以在特定情况下最大化奖励。强化学习与监督学习的不同之处在于，在监督学习中，训练数据具有答案，因此模型用正确答案本身训练，而在强化学习中，没有答案，代理人(agent)决定如何做执行给定的任务。 在没有训练数据集的情况下，必然要从其经验中学习。一个强化学习由以下几个部分组成。
（1）代理人agent：代理人就是行动者，例如象棋中的棋子，在机器学习中，算法就是agent
（2）动作action：action是代理人可以做出的所有可能行动的集合
（3）奖励（Reward）：奖励是我们衡量代理人行为成败的反馈
（4）贴现因子(discount factor)：是一个金融学名词，也称为折现系数，在金融学中，discount factor和年份以及汇率有关，在强化学习中，discount factor一般会用GAMMA来表示，称之为奖励的衰减值
（5）环境environment：代理人活动的范围
（6）状态state：是代理人当下具体的情况
（7）策略policy：代理人根据当前状态确定下一个操作的策略，策略通常用π来表示
（8）价值value：带有折扣的预期长期收益，而不是短期奖励
（9）Q_value：Q_value类似于value，但它需要一个额外的参数：当前动作a。 Qπ（s，a）指的是当前状态s的长期回报，在政策π下采取行动

2.强化学习的分类

(1)model-free和model-based

所有的强化学习都可以分为两大类，第一类是不理解环境（model-free），另外一类时理解环境（model-based）。model-free的方法有很多，Q Learning， Sarsa，Policy Gradients；model_based的方法和model-free一样，也是Q Learning， Sarsa，Policy Gradients，但对比model-free它多了一个想象力，在model-free中只能按部就班一步一步等待真实世界的反馈，再根据反馈采取下一步的方法，而在model-based中，可以通过想象来预判发生的所有情况，然后根据想象的情况来选择最好的那一种。


(2)policy-based和value-based

另外一种分类方法就是基于概率（policy-based）和基于价值（value-based）。基于价值能通过感官分析所处的环境，直接输出下一步采取各种行动的概率，然后根据概率采取行动，所有行动都有可能被选中，只是概率不同，基于概率有policy gradients。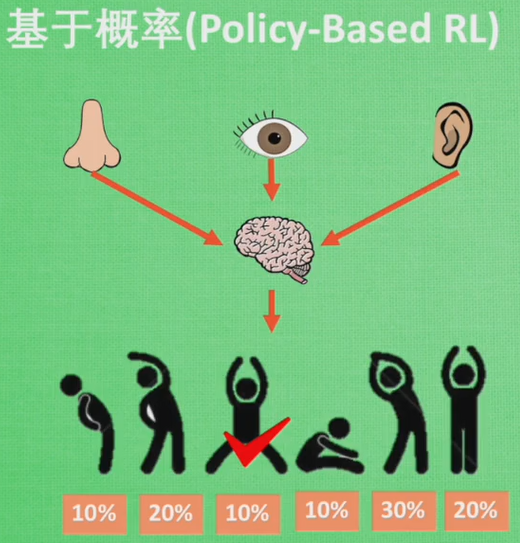
image.png
基于价值则是输出所有动作的价值，会根据最高价值来选择动作，相比基于概率，基于价值的选择更加铁定，毫不留情就选价值最高的，基于价值有Q learning 和 Sarsa。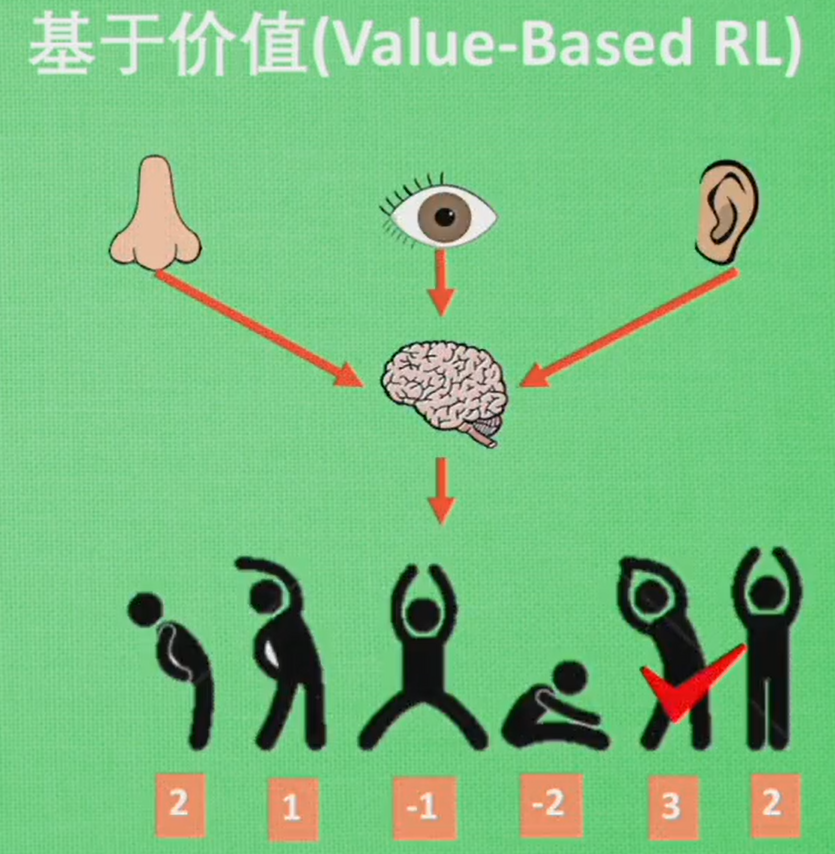
强化学习 - 图2

3.简单的Q learning 游戏代码

  1. # -*- coding: utf-8 -*-
  2. """
  3. @author: Haojie Shu
  4. @time: 2019/05/21
  5. @description: 简单的小游戏了解强化学习中的q_learning
  6. """
  8. import numpy as np
  9. import pandas as pd
  10. import time
  12. np.random.seed(2)  # 伪随机数,让随机数固定下来
  14. N_STATES = 6  # 由于起始位置和终止位置的距离为6,因此状态数为6
  15. ACTIONS = ['left', 'right']  # 走左边或者走右边
  16. EPSILON = 0.9  # 90%选择最优动作,10%选择随机动作
  17. ALPHA = 0.1  # 学习效率
  18. GAMMA = 0.9  # 奖励的衰减值
  19. MAX_EPISODES = 13  # 只玩13个回合
  20. FRESH_TIME = 0.3  # 走一步花的时间
  23. def build_q_table(n_states, actions):
  24.     """
  25.     建立q_table,并且用全0初始化它,最开始是一个全0的DataFrame
  26.     """
  27.     table = pd.DataFrame(
  28.         np.zeros((n_states, len(actions))),
  29.         columns=actions,
  30.     )
  31.     """
  32.         left  right
  33.     0   0.0    0.0
  34.     1   0.0    0.0
  35.     2   0.0    0.0
  36.     3   0.0    0.0
  37.     4   0.0    0.0
  38.     5   0.0    0.0
  39.     """
  40.     return table
  43. def choose_action(state, q_table):  # 选择动作
  45.     state_actions = q_table.iloc[state, :]  # q_table的某一行
  46.     # np.random.uniform:创建[low,high]的随机数,low默认值为0,high默认值为1,这样就可以保证10%的情况下会走这个if,随机选择左右
  47.     # 当DataFrame的某一行全部为0也会走这个if,这个if会随机选择左或者右
  48.     if (np.random.uniform() > EPSILON) or ((state_actions == 0).all()):
  49.         action_name = np.random.choice(ACTIONS)
  50.     else:
  51.         action_name = state_actions.idxmax()  # 选择q_table里面left或者right比较大的索引
  52.     return action_name
  55. def get_env_feedback(s, a):  # 环境对行为的反映
  56.     if a == 'right':  # 向右移动
  57.         if s == N_STATES - 2:   # 向右移动,并且如果s=4, 就会终止;因为再向右移动就是T了
  58.             s_ = 'terminal'
  59.             r = 1
  60.         else:
  61.             s_ = s + 1
  62.             r = 0
  63.     else:   # 向左移动
  64.         r = 0
  65.         if s == 0:
  66.             s_ = s  # reach the wall
  67.         else:
  68.             s_ = s - 1
  69.     return s_, r
  72. def update_env(s, episode, step_counter):  # 这个是为了展示用
  73.     env_list = ['-']*(N_STATES-1) + ['T']
  74.     if s == 'terminal':
  75.         interaction = 'Episode %s: total_steps = %s' % (episode+1, step_counter)
  76.         print('{}'.format(interaction))
  77.         time.sleep(2)
  78.     else:
  79.         env_list[s] = 'o'
  80.         interaction = ''.join(env_list)
  81.         print('{}'.format(interaction))
  82.         time.sleep(FRESH_TIME)
  85. def rl():
  86.     q_table = build_q_table(N_STATES, ACTIONS)  # 初始化q_table
  87.     for episode in range(MAX_EPISODES):  # 从第一个回合玩到最后一个回合
  88.         step_counter = 0  # 计步器
  89.         s = 0  # 初始时,将探索者放到最左边
  90.         is_terminated = False  # 是否终止
  91.         update_env(s, episode, step_counter)
  92.         while not is_terminated:  # 游戏没有终止就始终执行while循环
  93.             a = choose_action(s, q_table)  # 选择动作, 第一次由于全0,随机选择一个
  94.             print a  # 由于很多时候a都是随机的，最好打印一下动作a到底是左还是右
  95.             s_, r = get_env_feedback(s, a)  # 从动作中获取反馈
  96.             q_predict = q_table.loc[s, a]  # 估计值
  97.             if s_ != 'terminal':  # 没有终止
  98.                 q_target = r + GAMMA * q_table.iloc[s_, :].max()   #
  99.             else:
  100.                 q_target = r  # 下个回合终止
  101.                 is_terminated = True  # 断开while循环
  103.             q_table.loc[s, a] += ALPHA * (q_target - q_predict)  # 更新q_table
  104.             print q_table  # 每次看一下q_table到底是长什么样的
  105.             s = s_
  106.             update_env(s, episode, step_counter+1)
  107.             step_counter += 1
  108.     return q_table
  111. if __name__ == "__main__":
  112.     q_tables = rl()
  113.     print(q_tables)

游戏的重要过程说明如下：

第一个游戏回合episode=0
初始化q_tables
left right
0 0.0 0.0
1 0.0 0.0
2 0.0 0.0
3 0.0 0.0
4 0.0 0.0
5 0.0 0.0

（1）第一步：观察者在起始位置s=0，此时输出
o——T
游戏没有终止
a=right
s =1, r=0
q_predict =0
由于s !=terminal
qtarget = r+ 0.9 * q_table. iloc [s, :].max=0+0.90=0
更新q_table
q_table[0, right] = q_table[0, right] + ALPHA (q_target-q_predict) = 0+0.1*0 = 0
此时的q_table:
left right
0 0.0 0.0
1 0.0 0.0
2 0.0 0.0
3 0.0 0.0
4 0.0 0.0
5 0.0 0.0

s=s_=1
此时s=1,episode=1,stepcounter+1=1，此时输出
-o—-T
并且step_counter=1

（2）第二步，此时没有跳出while语句，此时s=1，此时由于仍然是全0，继续随机选一个a = right
s = s+1=2, r=0
q_predict = 0
q_target = 0 +0.9*0=0
更新q_table，此时的q_table
left right
0 0.0 0.0
1 0.0 0.0
2 0.0 0.0
3 0.0 0.0
4 0.0 0.0
5 0.0 0.0
此时s = s =2，此时输出
—o—T
step_counter=2

(3)第三步，此时由于qtable仍然是全0，随机选择 a= left
此时 r= 0，s=s-1 =1
q_predict = 0
q_target = 0+0.9*0
更新q_table，此时的q_table
left right
0 0.0 0.0
1 0.0 0.0
2 0.0 0.0
3 0.0 0.0
4 0.0 0.0
5 0.0 0.0

s =s_ =1，此时输出
-o—-T

……

（38）第38步，s=4，随机选择的a=right
此时s_=terminal，r=1
q_predict = q_tables. iloc [4, right]=0
此时q_target =1，is_terminated = True
q_tables[4, right] = 0+ 0.1*1=0.1
此时的q_tables
left right
0 0.0 0.0
1 0.0 0.0
2 0.0 0.0
3 0.0 0.0
4 0.0 0.1
5 0.0 0.0

此时s=s_=terminal，此时完成一个游戏回合

第二个游戏回合epidosde=1
（1）s=0，先输出o——T，此时qtables的第一行由于全0，因此仍然是执行随机选择action，此次的随机结果为left
此时r=0，s由于等于0，撞墙了，此时是s=s=0
qpredict =0，q_target=0
此时q_tables不改变，s也不改变
（2）再次来一遍，此时的action为right，
s=s+1=1，r=0
此时qpredict=0，q_target = r=0
此时的q_tables仍然不改变
s=s=1
（3）此时的action为left，
s = s-1 =0，r=0
此时q_predict=0，q_target = r=0
此时的q_tables仍然不改变
s=s=0
…
（21）第21步，s=3，此时的a为right
此时的s_=s+1，r=0
此时的q_predict=0，q_target =0+0.1*0.9=0.09
此时的q_tables为
left right
0 0.0 0.0
1 0.0 0.0
2 0.0 0.0
3 0.0 0.009
4 0.0 0.1
5 0.0 0.0

（22）第22步，s=4，随机选取的a为right
此时s_=terminal，r=1，此时的q_predict =q_table. iloc[4, right]=0.1
q_target=1, is_terminated=True
q_table[4,right]=0.1+0.1*（1-0.1）=0.19
此时的q_table
left right
0 0.0 0.0
1 0.0 0.0
2 0.0 0.0
3 0.0 0.009
4 0.0 0.19
5 0.0 0.0

此时完成第二个游戏回合

第三个游戏回合epidosde=2
（1）…
（2）…

…

（7）第7步，此时s=2，a=right
此时s_=s+1=3，r=0
此时q_predict=0，q_target=0+0.9*0.009=0.0081
此时的q_table为
left right
0 0.0 0.0
1 0.0 0.0
2 0.0 0.00081
3 0.0 0.009
4 0.0 0.19
5 0.0 0.0

（8）第8步，此时s=3
此时的actionname 不再100%是随机的了，随机的概率降到了10%！！！
此时的action_name会选择left或者right中，数字大的那个索引，即right
此时s=s+1=4，r=0
此时q_predict = 0.009，q_target = 0.9（0.19-0）= 0.171
q_table.loc [3, right] = 0.009+0.1(0.171- 0.009) = 0.017829=0.0252
此时的q_table
left right
0 0.0 0.0
1 0.0 0.0
2 0.0 0.00081
3 0.0 0.009
4 0.0 0.252
5 0.0 0.0

（9）第9步，结束这一局的游戏…