说明

排序(Sorting) 是计算机程序设计中的一种重要操作，它的功能是将一个数据元素（或记录）的任意序列，重新排列成一个关键字有序的序列。

概念

1. 比较排序
   在排序的最终结果里，元素之间的次序依赖于它们之间的比较。每个数都必须和其他数进行比较，才能确定自己的位置。

2. 非比较排序
   非比较排序是通过确定每个元素之前，应该有多少个元素来排序。

3. 稳定排序
   通俗地讲就是能保证排序前2个相等的数其在序列的前后位置顺序和排序后它们两个的前后位置顺序相同。如果a原本在b前面，而a=b，排序之后a仍然在b的前面；

4. 非稳定排序
   如果a原本在b的前面，而a=b，排序之后a可能会出现在b的后面。

5. 原地排序
   原地排序就是指在排序过程中不申请多余的存储空间，只利用原来存储待排数据的存储空间进行比较和交换的数据排序。

6. 非原地排序
   需要利用额外的数组来辅助排序。

7. 内排序
   所有排序操作都在内存中完成。

8. 外排序
   由于数据太大，因此把数据放在磁盘中，而排序通过磁盘和内存的数据传输才能进行。

• 比较排序

在冒泡排序之类的排序中，问题规模为n，又因为需要比较 n 次，所以平均时间复杂度为 O(n²) 。在归并排序、快速排序之类的排序中，问题规模通过分治法消减为 logN 次，所以时间复杂度平均 O(nlogn) 。

比较排序的优势是，适用于各种规模的数据，也不在乎数据的分布，都能进行排序。可以说，比较排序适用于一切需要排序的情况。

• 非比较排序

针对数组 arr，计算 arr[i] 之前有多少个元素，则唯一确定了 arr[i] 在排序后数组中的位置。 非比较排序只要确定每个元素之前的已有的元素个数即可，所有一次遍历即可解决。时间复杂度 O(n)。

非比较排序时间复杂度底，但由于非比较排序需要占用空间来确定唯一位置。所以对数据规模和数据分布有一定的要求。

分类

非线性时间比较类排序

通过比较来决定元素间的相对次序，由于其时间复杂度不能突破O(nlogn)，因此称为非线性时间比较类排序。

线性时间非比较类排序

不通过比较来决定元素间的相对次序，它可以突破基于比较排序的时间下界，以线性时间运行，因此称为线性时间非比较类排序。

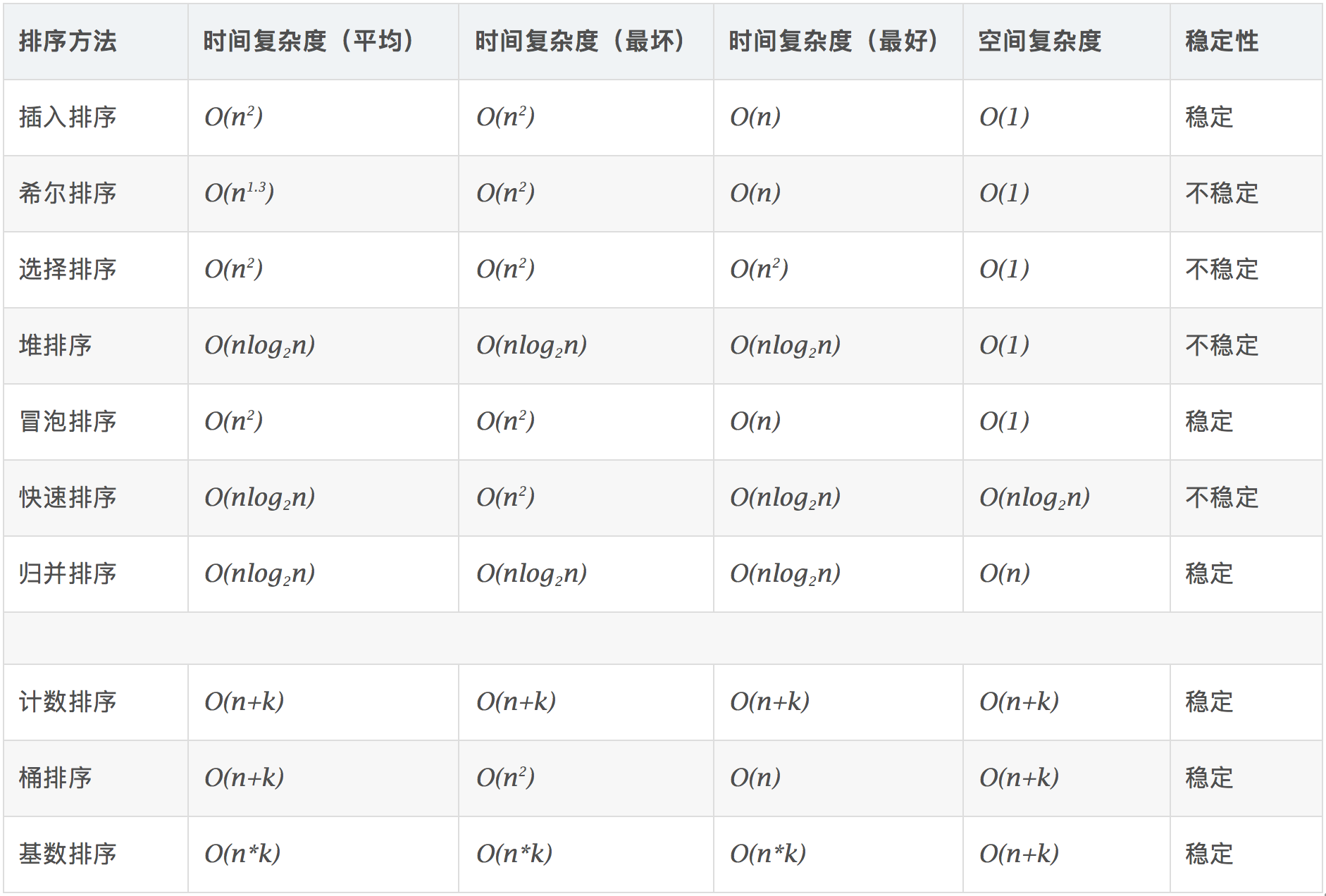
算法复杂度