1447:最简分数

题目地址：最简分数

解题思路

因为要求值要在(0,1)之内，所以分子要比分母小，根据示例，罗列了一下，当

n = 6

应该输出：

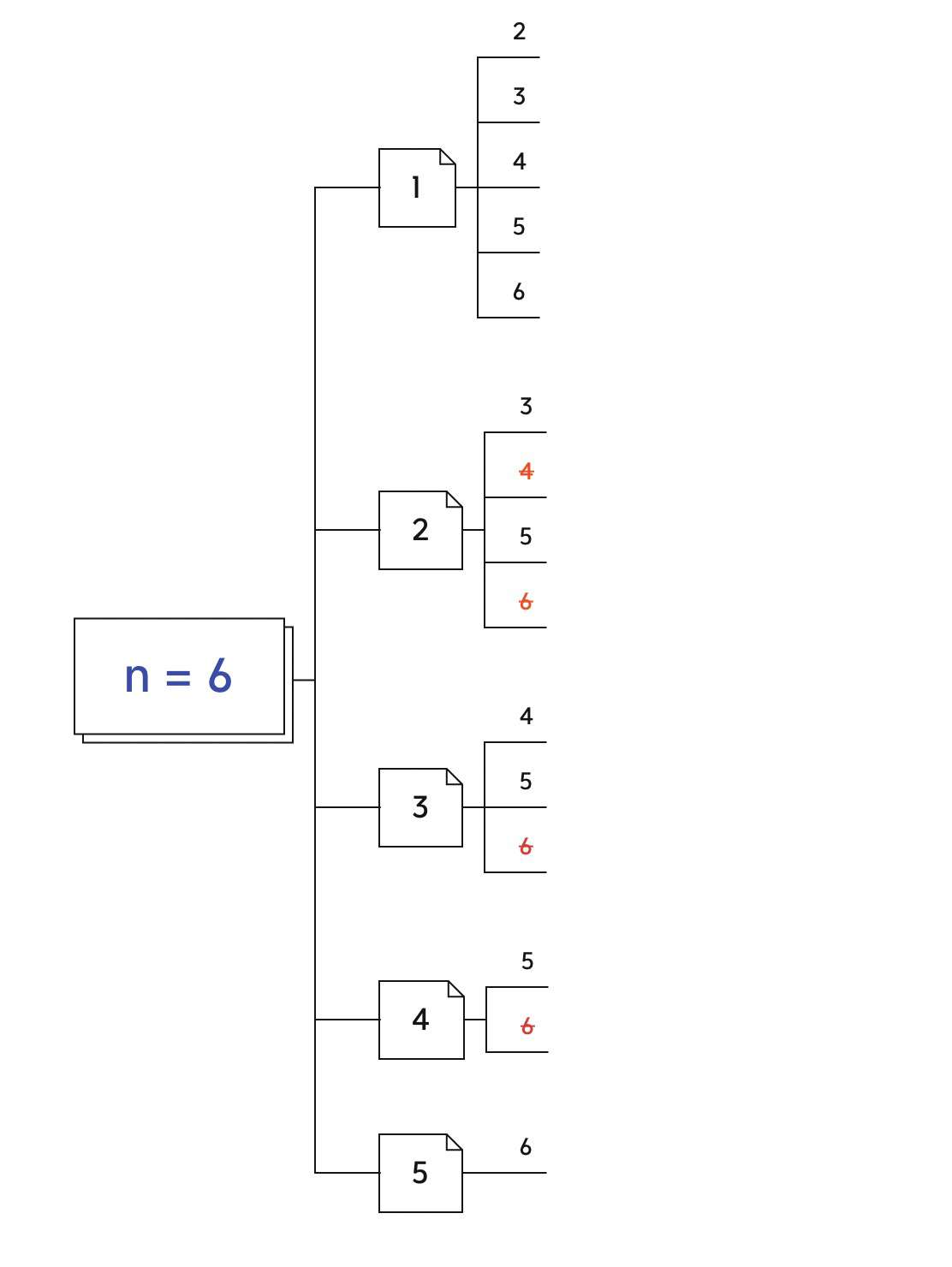
因为要求分子和分母是最简分数，也就是🈯️：分子和分母的最大公约数是1，所以第一版本代码

代码

/**
 * @param {number} n
 * @return {string[]}
 */
 var simplifiedFractions = function(n) {
     const result = [];
     if(n>1){
         for(let i = 1;i<n;i++){
             for(let j = i+1;j<=n;j++){
                let flag = false;
                 if(i !== 1){
                    let c = i;
                    while(c>1){
                        if(j % c == 0 && i % c == 0){
                            flag = true;
                            break;
                        }
                        c--;
                    }
                 }
                 if(!flag || i === 1){
                    result.push(`${i}/${j}`);
                 }
             }
         }
     }
     return result;
};
const key = 8;
console.log(simplifiedFractions(key));

官方题解

官方题解，在求取两个数的最大公约数时，可以用辗转相除（欧几里得算法）

var simplifiedFractions = function(n) {
    const ans = [];
    for (let denominator = 2; denominator <= n; ++denominator) {
        for (let numerator = 1; numerator < denominator; ++numerator) {
            if (gcd(numerator, denominator) == 1) {
                ans.push(numerator + "/" + denominator);
            }
        }
    }
    return ans;
};
const gcd = (a, b) => {
    if (b === 0) {
        return a;
    }
    return gcd(b, a % b);
}

证明如下：

假设a>b, a可以表示成a = kb + r（a，b，k，r皆为正整数，且r而r = a - kb，两边同时除以d，r/d=a/d-kb/d=m，由等式右边可知m为整数， 因此d|r 因此d也是b,a mod b的公约数
假设d是b,a mod b的公约数, 则d|b,d|(a-k*b),k是一个整数。进而d|a.因此d也是a,b的公约数 因此(a,b)和(b,a mod b)的公约数是一样的，其最大公约数也必然相等，得证

扩展

计算3个数的最大公约数

/***
*方法一：找到三个数中的最小的数，作为循环遍历的边界值
**/
const min = (a,b,c)=>{
    return Math.min(c,Math.min(a,b));
}
const gcdm = (a,b,c)=>{
    const n = min(a,b,c)
    if(n === 1) return n;
    let result = 1;
    for(let i = 2;i<=n;i++){
        if(a%i===0 && b%i === 0 && c%i === 0){
           result = i;  
        }
    }
    return result;
}
console.log(gcdm(9,6,12));
/***
*方法二：求出两个的最大公约数，再与第三个相求
**/
const gcd = (a, b) => {
    if (b === 0) {
        return a;
    }
    return gcd(b, a % b);
}
console.log(gcd(gcd(9,6),12));

类似习题：

找出数组中的最大公约数

总结

用辗转相除（欧几里得算法）计算两个数的最大公约数