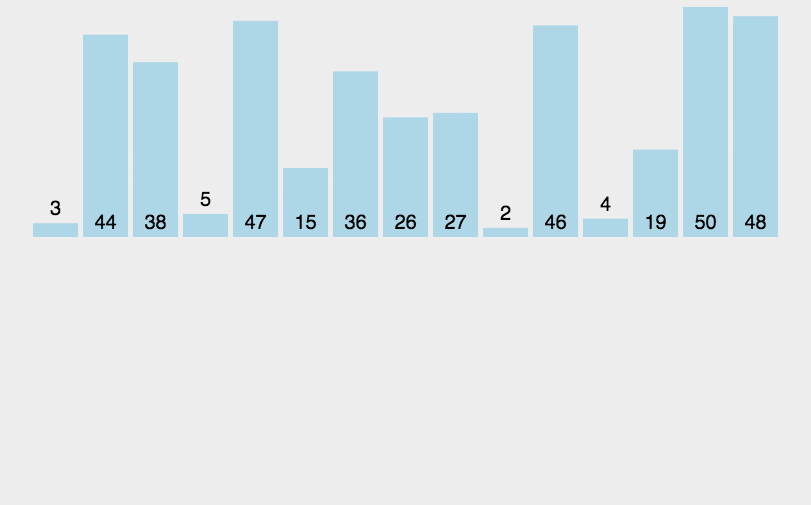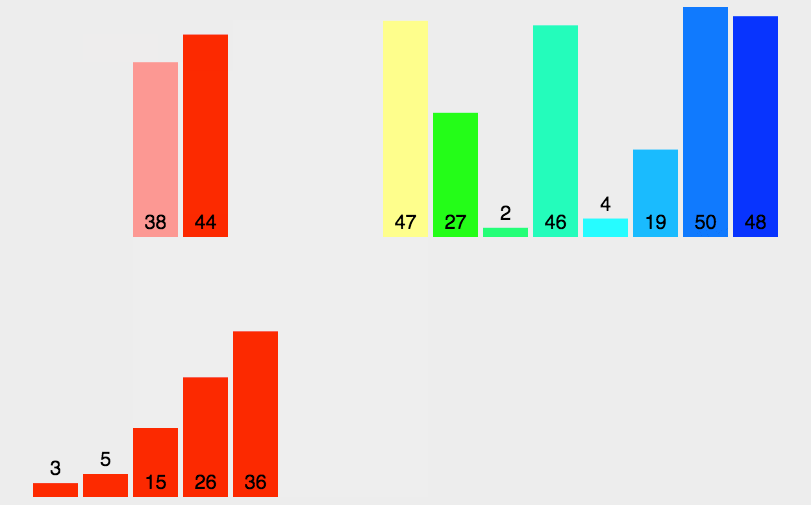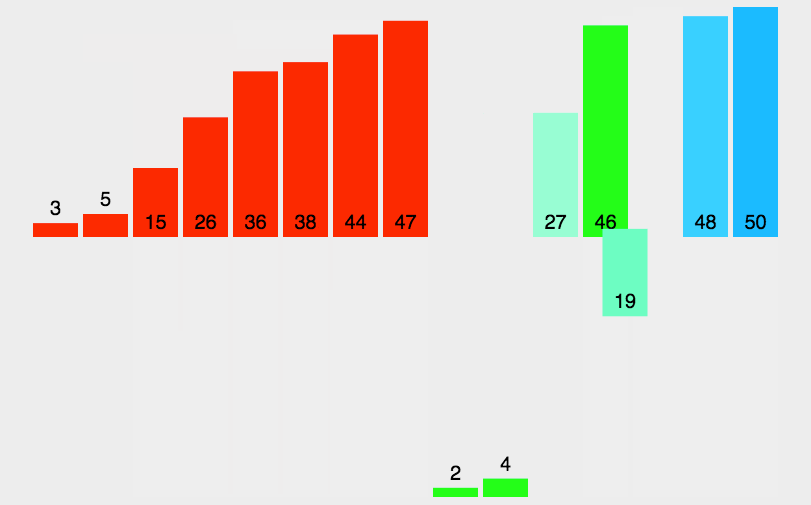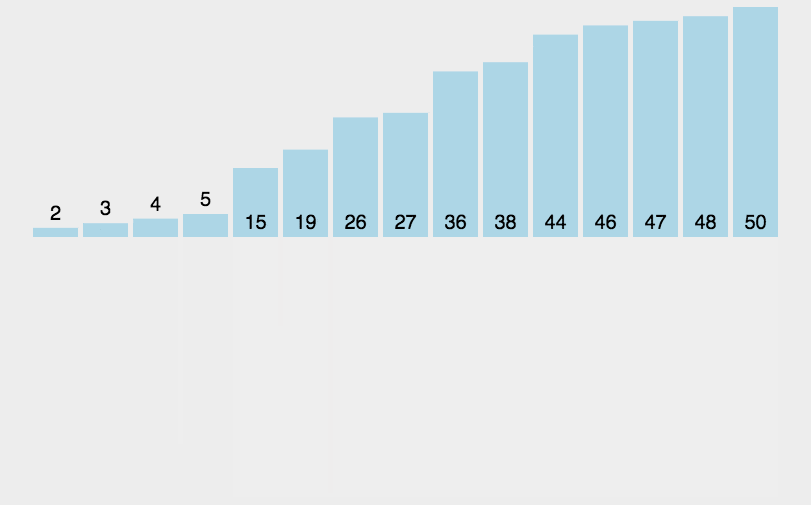
归并排序（Merge sort）

  • 平均时间复杂度：O(nlogn)
  • 最好情况：O(nlogn)
  • 最坏情况：O(nlogn)
  • 空间复杂度：O(n)
  • 排序方式：外部

  • 稳定性：稳定

    C++代码实现

    1. void Merge(vector<int> &arr, int lhs, int mid, int rhs) {
    2.   //优化一 
    3.   if(arr[mid-1]<=arr[mid]) return;
    4.   vector<int> tempArr={};
    5.   int l_pos = lhs;
    6.   int r_pos = mid;
    7.   while(l_pos<mid&&r_pos<rhs){
    8.       if(arr[l_pos] < arr[r_pos])
    9.           tempArr.push_back(arr[l_pos++]);
    10.       else
    11.           tempArr.push_back(arr[r_pos++]);
    12.   }
    14.   while(l_pos<mid){
    15.       tempArr.push_back(arr[l_pos++]);
    16.   }
    17.   while(r_pos<rhs){
    18.       tempArr.push_back(arr[r_pos++]);
    19.   }
    21.   for(const auto& val:tempArr){
    22.       arr[lhs++] = val;
    23.   }
    24. }
    25. void mergeSort(vector<int>& arr, int lhs, int rhs) {
    26.   if(lhs+1 >= rhs) return;
    27.   int mid = lhs+((rhs - lhs)>>1);
    28.   mergeSort(arr, lhs, mid); 
    29.   mergeSort(arr, mid, rhs);
    30.   Merge(arr, lhs, mid, rhs);  
    31. }

1. 算法步骤

  1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；
  2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置；
  3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；
  4. 重复步骤 3 直到某一指针达到序列尾；
  5. 将另一序列剩下的所有元素直接复制到合并序列尾。

    优化步骤

    ① 辅助数组作为参数传入，减少创建时间
    ② 对于较小规模的字序列排序，使用插入排序
    ③ 判断合并序列是否已经有序，如果arr[mid-1] <= arr[mid]，则有序跳过merge函数

2. 动图演示

mergeSort.gif