RefList：
https://blog.csdn.net/b285795298/article/details/81977271
https://blog.csdn.net/u012679707/article/details/80501358
周志华《机器学习》第六章

原理

线性分类任务：

给定训练样本集 D = {(X1 , Y1) ， (X2 ， Y2) , . . . , (Xm, Ym)} , Yi ∈{-1 ，+1}，分类学习最基本的想法就是基于训练集 D 在样本空间中找到一个划分超平面、将不同类别的样本分开但能将训练样本分开的划分超平面可能有很多，如图所示，我们应该努力去找到哪一个昵?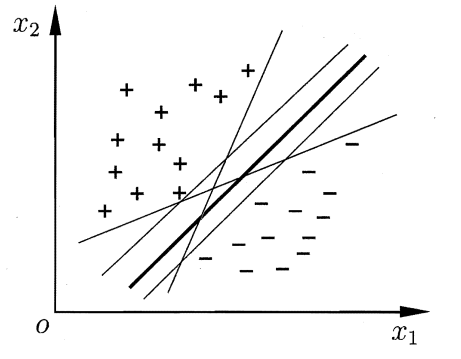
image.png
（存在多个划分）
我们直观感受是中间那根较粗的线是比较合适的划分，因为它对于两边的样本点的扰动并不“敏感”（比如左边的+的某个点稍微移动一下，这个划分仍然是一个合格的划分而不至于产生错误）

当然这是一个平面的划分任务，我们需要做的是在一个超平面上去找到这样的划分。
超平面的方程表示：
f(x)=wT·x+b=0
当f(x) 等于0的时候，x便是位于超平面上的点，而f(x)大于0的点对应 y=1 的数据点，f(x)小于0的点对应y=-1的点。某一个点与超平面的距离公式：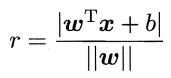
image.png
假设超平面(w,b)能将训练样本正确分类,即对于(xi,yi)∈D,若yi=+1,则有wT·xi+b>0;若yi=-1,则有wT·xi+b<0.令
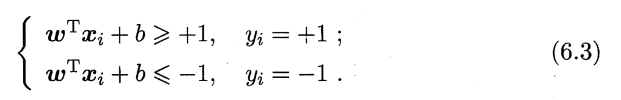
image.png
上式就是我们一个约束条件。

在这个条件下我们需要的是获得一个划分：对于这个划分的最近的点与它的距离要相对地远。这些最近的样本点叫做支持向量，两个异类支持向量到超平面的距离之和为：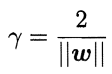
image.png
它就是“间隔”，附图解：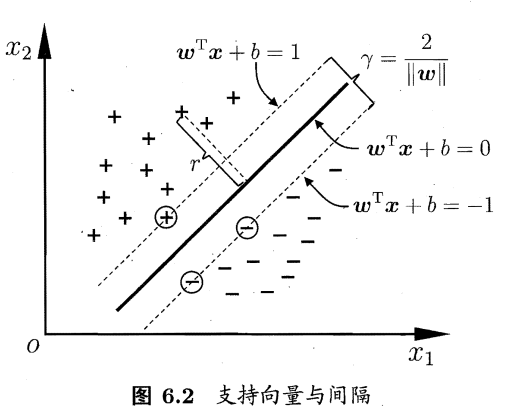
image.png
那么我们重申一下我们需要获得的东西：具有“最大间隔”的分类超平面
欲找到具有”最大间隔” (maximum margin) 的划分超平面，也就是要找到能满足式(6.3)中约束的参数w和b，使得间隔最大，即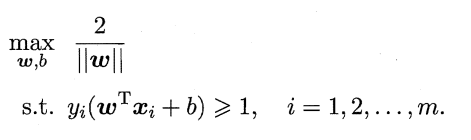
image.png
为了最大化间隔，仅需最小化||w||。于是，上式可重写为：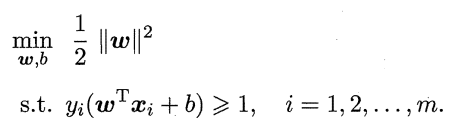
image.png
上式就是SVM的标准型。

对偶问题、SMO算法：

上面的问题中的 1/2||w||是凸函数，同时约束不等式是仿射函数，因此这是一个凸二次规划问题，根据凸优化理论，我们可以借助拉格朗日函数将我们的约束问题转化为无约束的问题来求解，我们的优化函数可以表达为：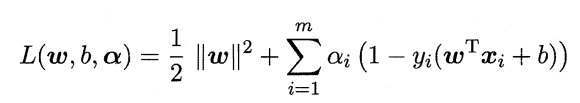
image.png

拉格朗日乘子αi >= 0
经过求偏导得出它的对偶问题：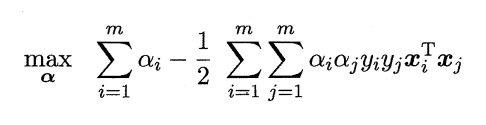
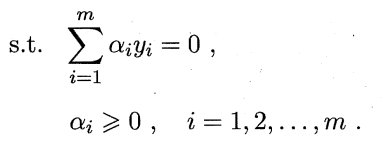
image.png
image.png
解出α后求出w与b即可得到模型：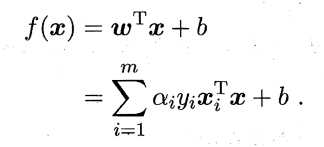
image.png (6.12)
KKT条件要求：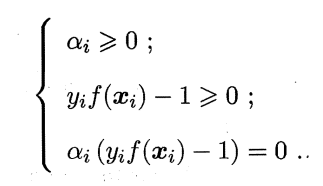
image.png
于是对任意训练样本(Xi，Yi) ， 总有：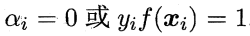
image.png
若αi = 0 ，则该样本将不会在式 (6.12) 的求和中出现，也就不会对 f(x) 有任何影响;若αi > 0, 则必有执f(Xi) = 1 ，所对应的样本点位于最大间隔边界上，是一个支持向量。
这显示出支持向量机的一个重要性质：训练完成后，大部分的训练样本都不需保留，最终模型仅与支持向量有关。

SMO：周志华《机器学习》P125

核函数：

我们希望训练样本是线性可分的，即存在一个划分超平面能将训练样本正确分类。然而在现实任务中，原始样本空间内，也许并不存在一个能正确划分两类样本的超平面。例如下图 6.3 中的” 异或 “ 问题就不是线性可分的。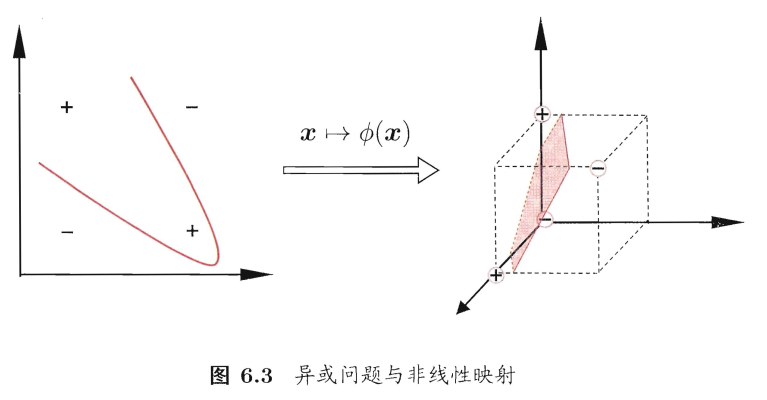
image.png
对于原空间中的非线性可分问题，可将样本从原始空间映射到一个更高维的特征空间，使得样本在这个特征空间内线性可分。例如在图6.3中，若将原始的二维空间映射到一个合适的三维空间 ，就能找到一个合适的划分超平面。幸运的是，如果原始空间是有限维，即属性数有限，那么一定存在一个高维特征空间使样本可分。令 g(x) 表示将 x 映射后的特征向量，于是， 在特征空间中划分超平面所对应的模型可表示为
f(x) = ω · g(x) + b
解决映射后的样本空间的问题需要计算一个复杂的式子：
image.png
这个函数就是核函数。此技巧也叫做核技巧。

常用的核函数有：线性核函数，多项式核函数，径向基核函数，Sigmoid核函数和复合核函数，傅立叶级数核，B样条核函数和张量积核函数。（核函数还需要满足对应核矩阵半正定的条件，过于理论不赘述）
事实上，对于一个半正定核矩阵，总能找到一个与之对应的映射Ф。换言之，任何一个核函数都隐式地定义了一个称为”再生核希尔伯特空间”的特征空间。
通过前面的讨论可知，我们希望样本在特征空间内线性可分，因此特征空间的好坏对支持向量机的性能至关重要。需注意的是，在不知道特征映射的形式时，我们并不知道什么样的核函数是合适的，而核函数也仅是隐式地定义了这个特征空间。于是，”核函数选择”成为支持向量机的最大变数。若核函数选择不合适，则意味着将样本映射到了一个不合适的特征空间，很可能导致性能不佳。
image.png
（这是一些经验）
image.png

软间隔：

在前面的讨论中，我们一直假定训练样本在样本空间或特征空间中是线性可分的，即存在一个超平面能将不同类的样本完全划分开。然而，在现实任务中往往很难确定合适的核函数使得训练样本在特征空间中线性可分。

退一步说，即使恰好找到了某个核函数使训练集在特征空间中线性可分，也很难断定这个貌似线性可分的结果不是由于过拟合所造成的。
那么如何缓解该问题呢？

缓解该问题的一个办法是：允许支持向量机在一些样本上出错。为此，引入”软间隔”的概念，如图 6.4所示：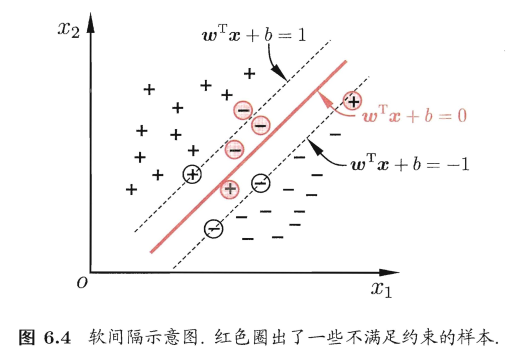
image.png

支持向量回归（SVR）：

image.png

优点：

第一个亮点：最大化间隔，最大化间隔能使得分类更加精确，且该最大间隔超平面是存在且唯一的。
第二个亮点：w，b 参数只与满足 y(wx + b) - 1 = 0 的样本有关，而这些样本点就是离最大间隔超平面最近的点，我们将这些点称之为支持向量。因此很多时候支持向量在小样本集分类时也能表现的很好，也正是因为这个原因。（另外需注意：α 向量的个数是和训练集数量相等的，对与大的训练集，会导致所需要的参数数量增多，因此SVM在处理大的训练集时会比其他常见的机器学习算法要慢）
第三个亮点：在不需要将样本映射到高维空间，而利用核函数解决非线性分类问题 。
**

实践：