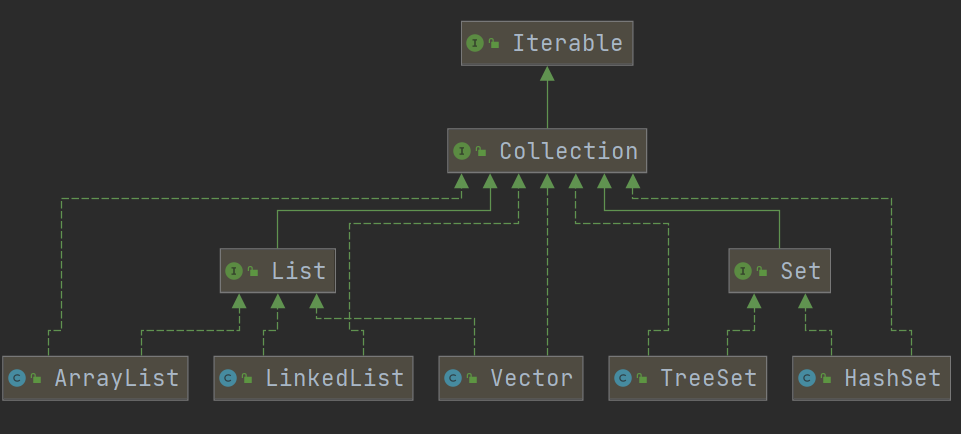
1.集合框架

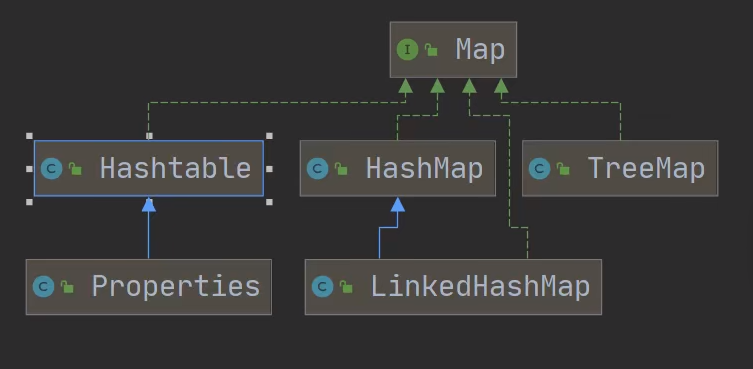
image.png

Map

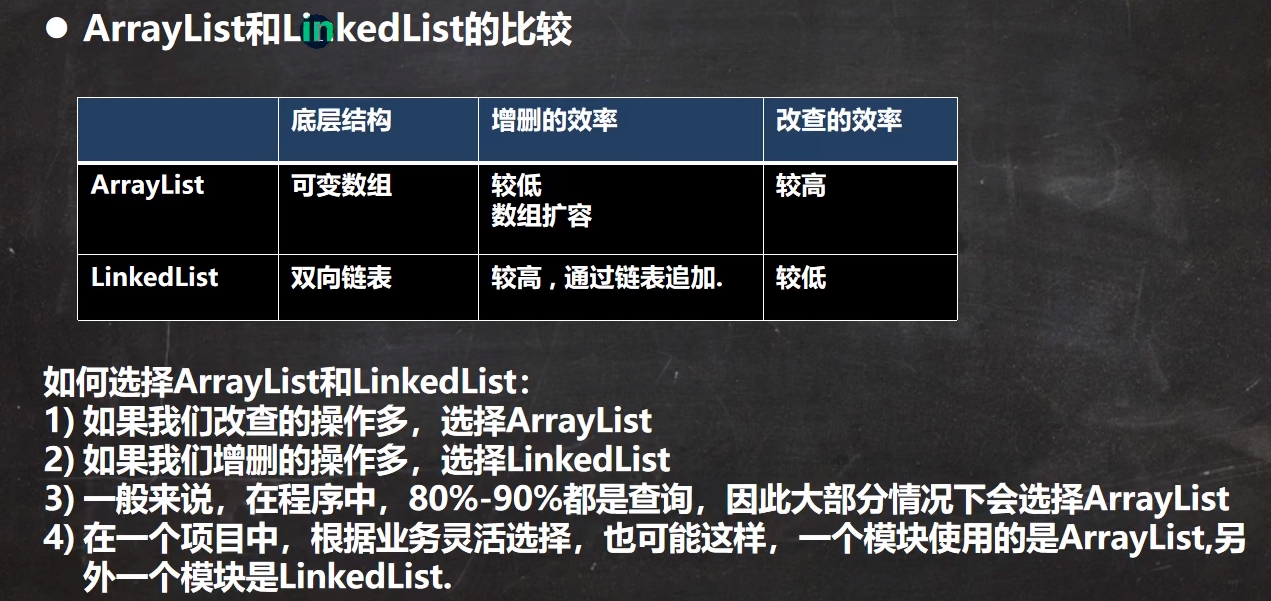
image.png

1.ArrayList

image.png

  1. 1.ArrayList的底层是一个Object的数组
  2.   第一次初始化是一个长度为0的空数组
  3.   transient Object[] elementData 不被序列化
  4.   private int size 每次存入一一个元素，size就会+1
  6. 2.默认的初始容量是0
  7.     第一次添加元素后容量为10
  8.     private void grow(int minCapacity) {
  9.         // overflow-conscious code
  10.         int oldCapacity = elementData.length;
  11.         int newCapacity = oldCapacity + (oldCapacity >> 1);
  12.         if (newCapacity - minCapacity < 0)
  13.             newCapacity = minCapacity;
  14.         if (newCapacity - MAX_ARRAY_SIZE > 0)
  15.             newCapacity = hugeCapacity(minCapacity);
  16.         // minCapacity is usually close to size, so this is a win:
  17.         elementData = Arrays.copyOf(elementData, newCapacity);  --//此处为第一次扩容
  18.     }
  19.   private static final int DEFAULT_CAPACITY = 10
  21. 3.拥有自动扩容机制，当元素大于当前容量时，会自动扩容，以保证list能够存放添加进去的元素。
  22.   每次扩容都是原来的(1.5)倍
  23.     int newCapacity = oldCapacity + (oldCapacity >> 1);
  25. 由于底层是一个数组，因而get和set方法都较为简单
  26. ·size() 方法可以获取list的容量
  27. ·set() 方法直接对指定位置进行赋值，且赋值前会进行角标越界检查
  28. ·get() 方法通过角标获得值，由于List是一个Object数组，故而获取后进行转换
  29. ·add() 方法可以添加一个元素

image.png

2.LinkedList

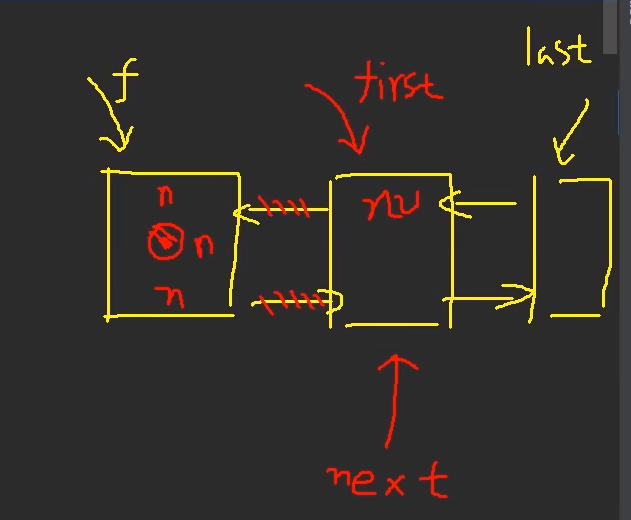
  1. 1.LinkedList是一个双向链表
  3.     transient Node<E> first;
  5.     transient Node<E> last;
  7.     private static class Node<E> {
  8.         E item;
  9.         Node<E> next;
  10.         Node<E> prev;
  12.         节点
  13.         Node(Node<E> prev, E element, Node<E> next) {
  14.             this.item = element;
  15.             this.next = next;
  16.             this.prev = prev;
  17.         }
  18.     }
  19.  ····添加
  20.  void linkLast(E e) {
  21.         final Node<E> l = last;
  22.         final Node<E> newNode = new Node<>(l, e, null);
  23.         last = newNode;
  24.         if (l == null)
  25.             first = newNode;
  26.         else
  27.             l.next = newNode;
  28.         size++;
  29.         modCount++;
  30.     }
  31. ····删除第一个
  32.  private E unlinkFirst(Node<E> f) {
  33.         // assert f == first && f != null;
  34.         final E element = f.item;
  35.         final Node<E> next = f.next;
  36.         f.item = null;
  37.         f.next = null; // help GC
  38.         first = next;
  39.         if (next == null)
  40.             last = null;
  41.         else
  42.             next.prev = null;
  43.         size--;
  44.         modCount++;
  45.         return element;
  46.     }
  47. 2.
  48. 初始为0
  49. transient int size = 0;
  50.      transient Node<E> first;
  51.      transient Node<E> last;

删除

image.png

3.HashMap

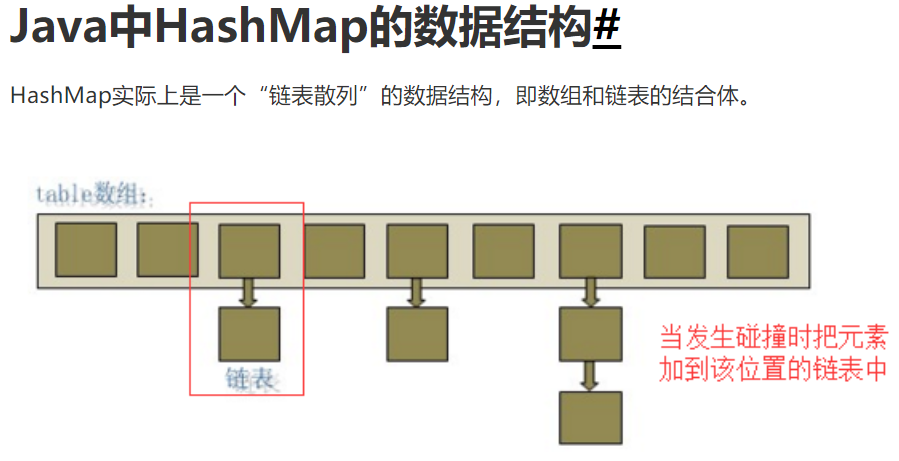
image.png
image.png

  1. 1.HashMap的默认容量为16
  2.     底层维护了一个transient Node<K,V>[] table; node数组
  3.     采用的数组+链表
  4.     每次扩容都是原来的(2)倍
  5. 2.加载因子为0.75，当元素大于等于容量的0.75倍时，就会进行扩容，是为了既要减少元素的碰撞，又充分利用空间
  6.     提高空间利用率和减少查询成本的折中，主要是泊松分布，0.75的话碰撞最小
  7. 3.如果key相同，后者的value就会覆盖掉前者的value，等价于替换
  8. 4.key-value中，key放在一个set集合，value放在一个collection集合
  9.     set不可重复，collection可重复
  10.     但是实际上key-value是存放在Node<hash,key,value,Node<K,V> next>中的key,value中
  11.     set和collection只是创建了一个引用指向了他们两个
  12.     主要是为了方便遍历key和value，还会创建一个EntrySet集合，这个集合存放的类型是Entry
  13.     而一个Entry对象就有有k，v EntrySet<Entry<key,value>> 即transient Set<Map.Entry<K,V>> entrySet
  14.     而Entry就是一个Node节点
  16. 详见HashSet

4.HashSet

  1. 1.HashSet底层是HashMap
  2. public HashSet() {
  3.         map = new HashMap<>();
  4.     }
  5. 2.元素不重复，可以存放空
  6. 3.数据无序，存放顺序和取出顺序可能不同，因为获得hash值后，在确定元素的索引
  7. 4.扩容
  8.     2倍扩容
  9. 5.为何相同元素添加不进去？
  10.     set.add("java")
  11.             1.执行add
  12.         private static final Object PRESENT = new Object()
  13.             PRESENT占位符
  14.             因为hashSet存放的并不是键值对，所以，map的value处都默认添加一个PRESENT占位符
  15.         public boolean add(E e) { e "java"
  16.                 return map.put(e, PRESENT)==null;
  17.             }
  18.             2.put方法
  19.         public V put(K key, V value) { key = "java"  value = PRESENT key是变化的，value不变，因为底层用的hashmap属于键值对，而这里相当于只添加键
  20.                                                                         故而值value为固定值
  21.                 return putVal(hash(key), key, value, false, true);
  22.             }
  23.                 2.1·hash（）方法
  24.                         先调用hashcode方法算出hash值h，再亦或其hash值并且无符号右移16位
  25.                         此处为字符串的hashCode方法
  26.                     public int hashCode() {
  27.                 int h = hash;
  28.                 if (h == 0 && value.length > 0) {
  29.                     char val[] = value;
  31.                     for (int i = 0; i < value.length; i++) {
  32.                         h = 31 * h + val[i];
  33.                     }
  34.                     hash = h;
  35.                 }
  36.                 return h;
  37.             }
  39.             return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16)
  40.                 因此，putVal()方法中的int hash并不是hashCode计算出的值
  41.                 这样主要是为了减少数据的碰撞
  42.             3.putVal()方法
  44.         final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
  45.                            boolean evict) {
  46.                 Node<K,V>[] tab; Node<K,V> p; int n, i;   --辅助变量
  47.                 if ((tab = table) == null || (n = tab.length) == 0)
  48.                             --如果当前table是null，或者大小为0，进行第一次扩容
  49.                             --table就是map的一个属性，是一个数组，用来存放节点
  50.                     n = (tab = resize()).length;
  51.                             --resize()后 tab和n就变成了16                                
  52.                 if ((p = tab[i = (n - 1) & hash]) == null)
  53.                           1.--根据传入的key，计算key的hash值，确认这个key该存放到table的那个索引
  54.                             --并且把这个位置的对象，赋给辅助变量p
  55.                           2.--判断这个p是不是空                                                   "java" PRESENT                
  56.                             --如果为空：表示还没有存放数据，就创建一个Node->tab[i] = newNode(hash, key, value, null)真正存放数据的节点
  57.                             --不为空：
  58.                     tab[i] = newNode(hash, key, value, null);
  59.                 else {
  60.                     Node<K,V> e; K k;
  61.                     if (p.hash == hash &&    --1..如果当前索引位置链表的第一个元素的hash==和准备添加的key的hash之一样，到2
  62.                                             --2.若满足以下两个条件之一
  63.                                                 --(1)准备加入的key和p指向的Node节点的Key是同一个对象
  64.                                                 --(2)不是用一个对象，但是内容相同
  65.                                             --不能加入
  66.                         ((k = p.key) == key || (key != null && key.equals(k))))
  67.                         e = p;
  68.                                 --判断p是不是一颗红黑树
  69.                     else if (p instanceof TreeNode)
  70.                         e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
  71.                     else {
  72.                                 --如果索引3是一个链表，有多个值，那么待添加的元素就和他们依次比较内容，如果不同就添加在最后一个的后面
  73.                                 --添加后判断节点数量是否为8，如果为8， 使用treeifyBin(tab, hash)把链表转为红黑树
  74.                                 --红黑树化时：如果数组长度<64不会进行树化，而是继续reSize，扩容后，再转化为红黑树
  75.                         for (int binCount = 0; ; ++binCount) {
  76.                             if ((e = p.next) == null) {
  77.                                 p.next = newNode(hash, key, value, null);
  78.                                 if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
  79.                                     treeifyBin(tab, hash);
  80.                                 break;
  81.                             }
  82.                                 --如果值一样，退出循环，比较下一个
  83.                             if (e.hash == hash &&
  84.                                 ((k = e.key) == key || (key != null && key.equals(k))))
  85.                                 break;
  86.                             p = e;
  87.                         }
  88.                     }
  89.                     if (e != null) { // existing mapping for key
  90.                         V oldValue = e.value;
  91.                         if (!onlyIfAbsent || oldValue == null)
  92.                             e.value = value;
  93.                         afterNodeAccess(e);
  94.                         return oldValue;
  95.                                 --返回空代表成功了
  96.                     }
  97.                 }
  98.                 ++modCount;
  99.                 if (++size > threshold)
  100.                             --首次扩容时的临界值threshold=12
  101.                             --如果++size后大于当前临界值，就进行resize()进行扩容
  102.                     resize();
  103.                 afterNodeInsertion(evict);
  104.                 return null;
  105.             }
  107.             4.reSize()方法
  108.             final Node<K,V>[] resize() {
  109.                     第一次时，table为空
  110.                 Node<K,V>[] oldTab = table;
  111.                 int oldCap = (oldTab == null) ? 0 : oldTab.length;
  112.                 int oldThr = threshold;
  113.                     --threshold是下一次更变大小的值，或者0
  114.                 int newCap, newThr = 0; --辅助变量
  116.                     oldCap首次为0，不进入该方法
  117.                 if (oldCap > 0) {
  118.                     if (oldCap >= MAXIMUM_CAPACITY) {
  119.                         threshold = Integer.MAX_VALUE;
  120.                         return oldTab;
  121.                     }
  122.                     else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
  123.                              oldCap >= DEFAULT_INITIAL_CAPACITY)
  124.                         newThr = oldThr << 1; // double threshold
  125.                 }
  126.                 else if (oldThr > 0) --需要更变大小的值
  127.                     newCap = oldThr;
  128.                 else {               --初始值为0
  129.                     newCap = DEFAULT_INITIAL_CAPACITY;
  130.                             --首次容量->DEFAULT_INITIAL_CAPACITY，为1<<<4 即初始容量为16     
  132.                     newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY); --他是扩容需要的临界值
  133.                             --DEFAULT_INITIAL_CAPACITY 加载因子，为0.75
  134.                             --临界值->newThr = 16*0.75        
  135.                 }
  136.                 if (newThr == 0) {
  137.                     float ft = (float)newCap * loadFactor;
  138.                     newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
  139.                               (int)ft : Integer.MAX_VALUE);
  140.                 }
  141.                 threshold = newThr;
  142.                 @SuppressWarnings({"rawtypes","unchecked"})
  143.                     Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
  144.                             --(Node<K,V>[])new Node[newCap] 创建一个长度为16的数组，并转成Node，并且把Node赋给newTab节点
  145.                 table = newTab;
  146.                             --把newTab赋值给table，此时table就有16个容量
  147.                 if (oldTab != null) {
  148.                     for (int j = 0; j < oldCap; ++j) {
  149.                         Node<K,V> e;
  150.                         if ((e = oldTab[j]) != null) {
  151.                             oldTab[j] = null;
  152.                             if (e.next == null)
  153.                                 newTab[e.hash & (newCap - 1)] = e;
  154.                             else if (e instanceof TreeNode)
  155.                                 ((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
  156.                             else { // preserve order
  157.                                 Node<K,V> loHead = null, loTail = null;
  158.                                 Node<K,V> hiHead = null, hiTail = null;
  159.                                 Node<K,V> next;
  160.                                 do {
  161.                                     next = e.next;
  162.                                     if ((e.hash & oldCap) == 0) {
  163.                                         if (loTail == null)
  164.                                             loHead = e;
  165.                                         else
  166.                                             loTail.next = e;
  167.                                         loTail = e;
  168.                                     }
  169.                                     else {
  170.                                         if (hiTail == null)
  171.                                             hiHead = e;
  172.                                         else
  173.                                             hiTail.next = e;
  174.                                         hiTail = e;
  175.                                     }
  176.                                 } while ((e = next) != null);
  177.                                 if (loTail != null) {
  178.                                     loTail.next = null;
  179.                                     newTab[j] = loHead;
  180.                                 }
  181.                                 if (hiTail != null) {
  182.                                     hiTail.next = null;
  183.                                     newTab[j + oldCap] = hiHead;
  184.                                 }
  185.                             }
  186.                         }
  187.                     }
  188.                 }
  189.                 return newTab;
  190.             }

首次添加元素Java，计算出hash值后，放在索引为3的位置

image.png

5.LinkedHashSet

链表的物理结构不一定和链表的逻辑结构一样，不同于顺序表

6.数据结构-简单二叉树的实现

  1. package datatest;
  3. /**
  4.  * @author 舞遍邓城一条街
  5.  */
  6. public class MyTreeTest {
  7.     public static void main(String[] args) {
  8.         TestTree testTree = new TestTree();
  9.         testTree.setRoot(new TestNode(22,"小宝"));
  10.         testTree.insert(new TestNode(18,"哈哈"));
  11.         testTree.insert(new TestNode(50,"小宝大大"));
  12.         testTree.insert(new TestNode(15,"小宝大大"));
  13.         testTree.insert(new TestNode(19,"小宝大大"));
  14.         testTree.delete(18);
  15.         testTree.preList();
  16.         System.out.println();
  17.         System.out.println(testTree.getNode(50));
  18.     }
  19. }
  20. @SuppressWarnings("all")
  21. class TestTree{
  22.     private TestNode root;
  24.     // 查找节点
  25.     public TestNode getNode(int id){
  26.         TestNode node = this.root;
  27.         while (node.getId()!=id){
  28.             if (node.getId()==id) {
  29.                 return node;
  30.             }
  31.             if (id>node.getId()) {
  32.                 node = node.getRight();
  33.             } else {
  34.                 node = node.getLeft();
  35.             }
  36.             if (node==null) {
  37.                 break;
  38.             }
  39.         }
  40.         return node;
  41.     }
  43.     // 插入节点
  44.     public void insert(TestNode node){
  45.         if (this.root==null){
  46.             root = node;
  47.         }else {
  48.             TestNode cur = this.root;
  49.             TestNode parent;
  50.             while (true){
  51.                 parent = cur;
  52.                 if (node.getId() < parent.getId()){  // 是否去左子树
  53.                     cur = cur.getLeft();
  54.                     if (cur == null){
  55.                         parent.left = node;
  56.                         return;
  57.                     }
  58.                 }else{ // 是否去右子树
  59.                     cur = cur.getRight();
  60.                     if (cur == null){
  61.                         parent.right = node;
  62.                         return;
  63.                     }
  64.                 }
  65.             }
  66.         }
  67.     }
  69.     // 查找最值
  70.     public TestNode getMin(){
  71.          TestNode last = null;
  72.          TestNode cur = this.root;
  73.          while (cur!=null){
  74.              last = cur;
  75.              cur = cur.left;
  76.          }
  77.         return last;
  78.     }
  79.     public TestNode getMax(){
  80.         TestNode last = null;
  81.         TestNode cur = this.root;
  82.         while (cur!=null){
  83.             last = cur;
  84.             cur = cur.getRight();
  85.         }
  86.         return last;
  87.     }
  89.     // 删除节点
  90.     public boolean delete(int id){
  91.         TestNode current = root;
  92.         TestNode parent = root; // 记录要删除节点的父节点
  93.         boolean isLeft = true;  // 判断这个节点在父节点的左边还是右边
  94.         while (current.getId()!=id){
  95.             parent = current;
  96.             if (id < current.getId()){
  97.                 isLeft = true;
  98.                 current = current.getLeft();
  99.             }else{
  100.                 isLeft = false;
  101.                 current = current.getRight();
  102.             }
  103.             if (current == null) {
  104.                 return false;  // 没有找到节点
  105.             }
  106.         }
  107.         // 找到了该节点
  108.         if (current.getLeft()==null && current.getRight()==null){
  109.             if (current == root){  // 如果是根节点
  110.                 root = null;
  111.             }else if (isLeft){ // 如果是左节点
  112.                 parent.left = null;
  113.             }else {  // 如果是右节点
  114.                 parent.right = null;
  115.             }
  116.             // 该节点没有右子节点，就让他的左子节点代当前节点
  117.         }else if (current.getRight()==null){
  118.             if (current == root){
  119.                 root = current.getLeft();
  120.             }else if (isLeft){
  121.                 parent.left = current.getLeft();
  122.             }else {
  123.                 parent.right = current.getLeft();
  124.             }
  125.             // 该节点没有左子节点，就让他的右子节点代当前节点
  126.         }else if (current.getLeft() == null) {
  127.             if (current == root) {
  128.                 root = current.getRight();
  129.             }else if (isLeft){
  130.                 parent.left = current.getRight();
  131.             }else {
  132.                 parent.right = current.getRight();
  133.             }
  134.             // 该节点有两个节点，就需要判断再决定让那个节点代替他
  135.         } else {
  136.             // 先查找该节点的后继节点
  137.             TestNode success = getSuccess(current);
  138.             if (current == root) {
  139.                 root = success;
  140.             } else if (isLeft) {
  141.                 parent.left = success;
  142.             }else {
  143.                 parent.right = success;
  144.             }
  145.             // 让该后继节点的左子树指向原来节点的左子树
  146.             success.left = current.getLeft();
  147.         }
  148.         return true;
  149.     }
  150.     // 找要删除节点的后继节点
  151.     private TestNode getSuccess(TestNode delnode){
  152.         TestNode successParent = delnode;
  153.         TestNode success = delnode;
  154.         // 去右子树查找后继节点
  155.         TestNode current = delnode.getRight();
  156.         while (current!=null){
  157.             // 记录当前节点的父节点
  158.             successParent = success;
  159.             // 记录当前节点
  160.             success = current;
  161.             current = current.getLeft();
  162.         }
  163.         if (success != delnode.getRight()){
  164.             successParent.left = success.getRight();
  165.             successParent.right = success.getRight();
  166.         }
  167.         return success;
  168.     }
  171.     // 遍历树
  172.     public void preList(){
  173.         if (this.root!=null){
  174.             this.root.preList();
  175.         }else {
  176.             System.out.println("树为空");
  177.         }
  178.     }
  179.     public void midList(){
  180.         if (this.root!=null){
  181.             this.root.midList();
  182.         }else {
  183.             System.out.println("树为空");
  184.         }
  185.     }
  186.     public void postList(){
  187.         if (this.root!=null){
  188.             this.root.postList();
  189.         }else {
  190.             System.out.println("树为空");
  191.         }
  192.     }
  195.     public TestTree() {
  196.     }
  197.     public TestNode getRoot() {
  198.         return root;
  199.     }
  200.     public void setRoot(TestNode root) {
  201.         this.root = root;
  202.     }
  203. }
  204. @SuppressWarnings("all")
  205. class TestNode{
  206.     public int id;
  207.     public String name;
  208.     public TestNode left;
  209.     public TestNode right;
  211.     // 前序遍历
  212.     public void preList(){
  213.         System.out.println(this);
  214.         if (this.left!=null) {
  215.             this.left.preList();
  216.         }
  217.         if (this.right!=null) {
  218.             this.right.preList();
  219.         }
  220.     }
  221.     // 中序遍历
  222.     public void midList(){
  223.         if (this.left!=null) {
  224.             this.left.midList();
  225.         }
  226.         System.out.println(this);
  227.         if (this.right!=null) {
  228.             this.right.midList();
  229.         }
  230.     }
  231.     // 后序遍历
  232.     public void postList(){
  233.         if (this.left!=null) {
  234.             this.left.postList();
  235.         }
  236.         if (this.right!=null) {
  237.             this.right.postList();
  238.         }
  239.         System.out.println(this);
  240.     }
  242.     @Override
  243.     public String toString() {
  244.         return "TestNode{" +
  245.                 "id=" + id +
  246.                 ", name='" + name + '\'' +
  247.                 '}';
  248.     }
  249.     public TestNode() {}
  250.     public TestNode(int id, String name) {
  251.         this.id = id;
  252.         this.name = name;
  253.     }
  254.     public int getId() {
  255.         return id;
  256.     }
  257.     public void setId(int id) {
  258.         this.id = id;
  259.     }
  260.     public String getName() {
  261.         return name;
  262.     }
  263.     public void setName(String name) {
  264.         this.name = name;
  265.     }
  266.     public TestNode getLeft() {
  267.         return left;
  268.     }
  269.     public TestNode getRight() {
  270.         return right;
  271.     }
  272. }