什么是二进制？

在了解二进制前我们要了解“**进制**”这个概念。进制是进位计数制的一个概念，**“N进制”即代表遇到(N)就向前进一位。**我们日常中使用的数字通常是**十进制数，即逢十进一**。通过这个概念以此类推，我们便能得到二进制、三进制……直到N进制。所以说不同进制之间的区别便是一位数上的最大值不同，是对同一个数字的不同表示方式，并且进制并不只有**二，八，十，十六**四种，只是这四种比较常用而已。<br />    而二进制便是现代计算机中普遍应用的一种进制，原因便是二进制每一位上只有两个数：0或1，这使得二进制数在物理层面上更容易表达以及运算，也为电路中的逻辑运算提供了便利。

进制的转换

初中的时候我们便学习过二进制与十进制的互换。<br />    十进制转换为二进制的方法称为除2取余法，即每次将整数部分除以2，余数为该位权上的数，而商继续除以2，余数又为上一个位权上的数，这个步骤一直持续下去，直到商为0为止，最后读数时候，从最后一个余数读起，一直到最前面的一个余数。<br />如图所示，十进制的500转换为二进制后就变为了`111110100(2)`。十进制转换为其他进制将除数2换成其他进制的值即可。<br />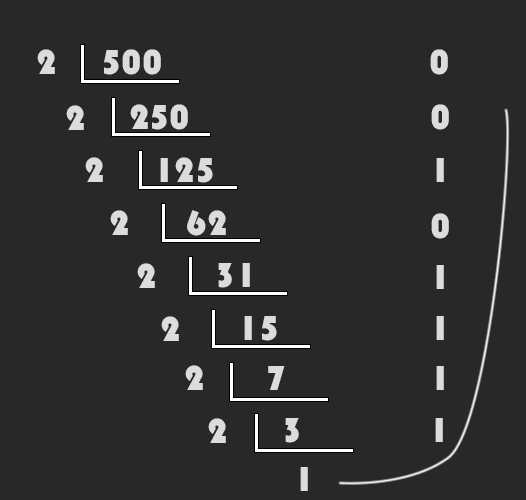![image.png](https://cdn.nlark.com/yuque/0/2021/png/21803058/1631858480990-c23b005f-da8f-4373-80a2-653564725fa1.png#clientId=u03af2802-e4b9-4&from=paste&id=ua175ce0b&margin=%5Bobject%20Object%5D&name=image.png&originHeight=500&originWidth=526&originalType=url&ratio=1&size=39736&status=done&style=none&taskId=u754236b1-741f-4671-a065-fcc743efc46)<br />

不同进制在代码中的表示方法

表示方法

二进制：0b*****    （例如：0b11001001 -> 201(10)）</li>
八进制：0******    （例如：0757 -> 495(10)）</li>
十进制：*******    （例如：551）</li>
十六进制：0x***    （例如：0xaf58 -> 44888(10)）</li>
十六进制：0X***    （例如：0xaf58 -> 44888(10)）</li>
//读者请注意，标准的C语言并不支持上面的二进制写法，
//只是有些编译器自己进行了扩展，才支持二进制数字。
//换句话说，并不是所有的编译器都支持二进制数字，
//只有一部分编译器支持，并且跟编译器的版本有关系。

在C语言中，我们支持进制输入和输出

八进制：%o输入必须为有效八进制数
十进制：%d
十六进制：%x输入必须为有效十六进制数
八进制：%o, %#o(推荐) 77, 077
十进制：%d, %ld
十六进制：%x, %X, %#x, %#X（推荐） 6f, 6F, 0x6f, 0X6F

下面来详细说说(注意：以下内容仅做扩展阅读)

C语言中常用的整数有 short、int 和 long 三种类型，通过 printf 函数，可以将它们以八进制、十进制和十六进制的形式输出。十进制已经很熟悉了，这里重点讲解如何以八进制和十六进制的形式输出，下表列出了不同类型的整数、以不同进制的形式输出时对应的格式控制符：

	short	int	long
八进制	%ho	%o	%lo
十进制	%hd	%d	%ld
十六进制	%hx 或者 %hX	%x 或者 %X	%lx 或者 %lX

十六进制数字的表示用到了英文字母，有大小写之分，要在格式控制符中体现出来：

%hx、%x 和 %lx 中的x小写，表明以小写字母的形式输出十六进制数；
%hX、%X 和 %lX 中的X大写，表明以大写字母的形式输出十六进制数。

八进制数字和十进制数字不区分大小写，所以格式控制符都用小写形式。如果你比较叛逆，想使用大写形式，那么行为是未定义的，请你慎重：

有些编译器支持大写形式，只不过行为和小写形式一样；
有些编译器不支持大写形式，可能会报错，也可能会导致奇怪的输出。

注意，虽然部分编译器支持二进制数字的表示，但是却不能使用 printf 函数输出二进制，这一点比较遗憾。当然，通过转换函数可以将其它进制数字转换成二进制数字，并以字符串的形式存储，然后在 printf 函数中使用%s输出即可。考虑到读者的基础可能还不够，这里就先不讲这种方法了。
那么请看以下示例：

#include <stdio.h>
int main()
{
    short a = 0b1010110;  //二进制数字
    int b = 02713;  //八进制数字
    long c = 0X1DAB83;  //十六进制数字
    printf("a=%ho, b=%o, c=%lo\n", a, b, c);  //以八进制形似输出
    printf("a=%hd, b=%d, c=%ld\n", a, b, c);  //以十进制形式输出
    printf("a=%hx, b=%x, c=%lx\n", a, b, c);  //以十六进制形式输出（字母小写）
    printf("a=%hX, b=%X, c=%lX\n", a, b, c);  //以十六进制形式输出（字母大写）
    return 0;
}
//以下为运行结果：
a=126, b=2713, c=7325603
a=86,  b=1483, c=1944451
a=56,  b=5cb,  c=1dab83
a=56,  b=5CB,  c=1DAB83

输出时加上前缀

请读者注意观察上面的例子，会发现有一点不完美，如果只看输出结果：

对于八进制数字，它没法和十进制、十六进制区分，因为八进制、十进制和十六进制都包含 0~7 这几个数字。
对于十进制数字，它没法和十六进制区分，因为十六进制也包含 0~9 这几个数字。如果十进制数字中还不包含 8 和 9，那么也不能和八进制区分了。
对于十六进制数字，如果没有包含 a~f 或者 A~F，那么就无法和十进制区分，如果还不包含 8 和 9，那么也不能和八进制区分了。
区分不同进制数字的一个简单办法就是，在输出时带上特定的前缀。在格式控制符中加上#即可输出前缀，例如 %#x、%#o、%#lX、%#ho 等，请看下面的代码：
```
#include <stdio.h>
int main()
{
  short a = 0b1010110;  //二进制数字
  int b = 02713;  //八进制数字
  long c = 0X1DAB83;  //十六进制数字
  printf("a=%#ho, b=%#o, c=%#lo\n", a, b, c);  //以八进制形似输出
  printf("a=%hd, b=%d, c=%ld\n", a, b, c);  //以十进制形式输出
  printf("a=%#hx, b=%#x, c=%#lx\n", a, b, c);  //以十六进制形式输出（字母小写）
  printf("a=%#hX, b=%#X, c=%#lX\n", a, b, c);  //以十六进制形式输出（字母大写）
  return 0;
}
//以下为运行结果：
a=0126, b=02713, c=07325603
a=86,   b=1483,  c=1944451
a=0x56, b=0x5cb, c=0x1dab83
a=0X56, b=0X5CB, c=0X1DAB83
```
注意：十进制数字没有前缀，所以不用加#。如果你加上了，那么它的行为是未定义的，有的编译器支持十进制加#，只不过输出结果和没有加#一样，有的编译器不支持加#，可能会报错，也可能会导致奇怪的输出；但是，大部分编译器都能正常输出，不至于当成一种错误。
数字运算
所有进制的运算依然符合小学所学的十进制运算方法，直接套用即可。
（但是请注意，逢几进几）
请看下面示例：二进制举例 ```c 数字： 111101 数字： × 110

运算： 000000 运算： 111101

运算： 111101

求解： 101101110

<a name="QGICZ"></a>
# 数字的二进制表示
<a name="pACNP"></a>
## 表示规则
    每一个二进制数被称为一位，这个数字有几个二进制数就占用几位。同时二进制数的最左端为最高位，最右端为最低位，即从右往左数，第一个数下标最小（0）。<br />二进制中正负数是怎么区分的呢？重点就在最高位上，当最高位为0时表示这是一个正数，当最高位为1时表示这是一个负数。当然也有例外，就是`unsigned ?`型的数据，这种数据不把最高位当作正负号的判定，而是将其也用来存储数字，这样做将数据的表示范围扩大了2倍，但同时也丧失了表示负数的能力。
<a name="lRU3p"></a>
## 原码
    顾名思义，原码就是数字原本的码值，任何数的原码就是其本身。
<a name="RRBMQ"></a>
## 反码
    反码比原码复杂一点，正数的反码是它本身，而负数的反码则是将除最高位的数外其它所有数反转，即0变成1，1变成0。比如：`0b10111`的反码便是`0b11000`
<a name="dxtUc"></a>
## 补码
    正数依旧延续传统，其补码仍是其本身。
<a name="G7EqD"></a>
### 负数的补码
    负数的补码有很多种求法，这里列出两种：<br />1.尾数的第一个‘1’及其右边的‘0’保持不变，左边的各位按位取反，符号位不变。例如：`0b111010`变成反码就是从右往左数第一个1以及其右边的0和符号位保持不变，其它位单独求反，就变成了`0b100110`。<br />2.将负数的反码+1。例如：`0b111010`的反码是`0b100101`，加一就变成了`0b100110`。<br />为什么这里要列出两个方法呢？因为第二个方法在网上广为流传，甚至被误认为其就是补码的定义，其实这只不过是补码凑巧等于反码+1而非因为反码+1是补码。如果你有兴趣了解这方面的知识，可以阅读《计算机组成原理》，其中更为详细且严谨的方式解释补码。
<a name="GxsCT"></a>
### 反码与补码的意义
    很多人可能会疑惑：为什么要创造补码这个概念？补码存在的意义是什么？为什么不直接用原码存储负数？<br />现在假设只存在原码，很好，现在的概念非常简单，我们来做数学运算吧。
```c
0101 + 0010 + 0101 = 1100 -> (5 + 2 + 5 = 15) //没问题
0000 + 1000 = 1000 -> (0 + (-0) = -0) //也没啥问题
0011 - 0010 = 0001 -> (3 - 2 = 1) //完全正确
1001 + 1001 = 0010 -> ((-1) + (-1) = 2) //啊？
0010 + 1010 = 1100 -> (2 + (-2) = -4) //?????
0011 + 1100 = 1111 -> (3 + (-4) = -7) //wtf?

最后几个等式仿佛在逗我们玩一样，甚至我们都不能称之为等式，因为他左右根本就不相等。仔细观察我们会发现，正数运算都很正常，但是一旦牵扯到负数就会出现各式各样的问题。所以原码，虽然直观易懂，易于正值转换。但用来实现加减法的话，运算规则总归是太复杂。于是反码来了。<br />    反码解决的问题是原码相反数相加不等于0的问题，现在让我们使用反码来进行一波计算。

0101 + 0010 + 0101 = 1100 -> (5 + 2 + 5 = 15) //没问题
0000 + 1111 = 1111 -> (0 + (-0) = -0) //也没啥问题
0011 - 0010 = 0001 -> (3 - 2 = 1) //完全正确
1110 + 1110 = 1100 -> ((-1) + (-1) = -3) //啊？
0010 + 1101 = 1111 -> (2 + (-2) = -0) //可以接受
0011 + 1011 = 1110 -> (3 + (-4) = -1) //正确

可正负数的加法问题解决了，但是负数与负数的运算依然是错误的。但是实际上，两个负数相加出错其实问题不大。我们的初衷是解决正与负的加法问题，虽然现在负负相加是错误的，但是正负数的差别只有符号位不同，如果想要运算负负相加只需要把两个负数转换为其原码并把符号位变成0，当作正数相加，再把符号位变成1就可以了。
到这里，我们已经解决了数字运算的问题，但是依然存在一个小问题，就是0010 + 1101 = 1111，为什么2 + (-2) 等于-0而不是0呢？虽然+0和0都一样，但是在小的问题也是问题，让我们来尝试解决它。
解决思路很简单，把负数的反码+1，这样就不存在-0了，而数字的表达范围也从[-2^(n-1), 2^(n-1)]拓展到了[-2^(n-1)-1, 2^(n-1)]。注意：这里的解决思路是从反码与补码这个巧合的关系推出来的，不是说补码就是由反码+1推出来的。会疑惑：为什么要创造补码这个概念？补码存在的意义是什么？为什么不直接用原码存储负数？

补码的优点

补码的存在，可以将符号位和数值域统一处理，同时让计算机可以使用加法运算来解决减法问题，这样硬件层面只需要有加法器就可以了，而不需要添加减法器，简化了电路设计。

位运算

&（and,和运算,二元）

and运算通常用于二进制的取位操作，例如一个数 and 1的结果就是取二进制的最末位。这可以用来判断一个整数的奇偶，二进制的最末位为0表示该数为偶数，最末位为1表示该数为奇数（Eg：快速奇偶判断）

#include<stdio.h>
int main()
{
    int n;
    scanf("%d",&n);
    n&1?printf("odd"):printf("even");
}

其原理为“相同位的两个数字都为1，则为1(True)；若有一个不为1，则为0(False)”
举个栗子：
20：10100 20:10100
01：00001 04:00100
—————— —————-
re：00000 re:00100
10= 0 10= 4

|（or,或运算，二元）

（相同位只要一个为1即为1）
or运算通常用于二进制特定位上的无条件赋值，例如一个数or 1的结果就是把二进制最末位强行变成1。
在这里你会发现一个有意思的东西：在某些情况(其实就是不进位的情况下)下a+b 和 a|b是等价的
153:10011001
102:01100110
| =255
如果需要把二进制最末位变成0，对这个数or 1之后再减一就可以了，其实际意义就是把这个数强行变成最接近的偶数。

var a = 103;
var c = (a | 1) - 1;//注意优先级
console.log(c);

控制台输出：102
103：1100111
| 1 : 1100111
-1 : 1100110

xor，异或运算 ^（二元）

按位异或运算, 对等长二进制模式按位或二进制数的每一位执行逻辑按位异或操作，操作的结果是如果某位不同则该位为1, 否则该位为0.（相同位不同则为1，相同则为0）
00101
11100
———-
11001

xor运算的逆运算是它本身，也就是说两次异或同一个数最后结果不变，即(a xor b) xor b = a。xor运算可以用于简单的加密，比如我想对我MM说1314520，但怕别人知道，于是双方约定拿我的生日19880516作为密钥。1314520 xor 19880516 = 20665500，我就把20665500告诉MM。MM再次计算20665500 xor 19880516的值，得到1314520。

在不进位的情况下，xor,or的运行结果相同~

var a = 2;
var b = 153 ^ 102;
console.log(b);
//输出225

not，非运算 ~（一元）

not运算的定义是把内存中的0和1全部取反。
使用not运算时要格外小心，你需要注意整数类型有没有符号。如果not的对象是无符号整数（不能表示负数），那么得到的值就是它与该类型上界的差，因为无符号类型的数是用00到$FFFF依次表示的。
下面程序返回65535-100=65435:

#include<stdio.h>
int main()
{
    unsigned short a=100;
    a=~a;
    printf("%d\n",a);
    return 0;
}

~的使用技巧：
记得!=EOF吗，关于代码”if(scanf("%d",n)!=EOF)“,它可以写成”if(~scanf("%d",n))“
因为scanf如果没有输入值就是返回-1，对于-1取反，则为0，0 == false
这里注意，布尔类型和数字类型的非运算符号不一样，布尔类型是!，数字类型是~。

shr，右移运算 >>（二元）

a shr b表示二进制右移b位（去掉末b位）
举个栗子：
运行这段代码：

var b = 985;
b >>= 1;
console.log(b);

控制台会输出：492，原理如下
985：1111011001
>>1
492： 0111101100
可以看到，985的二进制想右位移1位，高位用0补齐了；
&与>>的运用
可用来取整数n的二进制数的第k位数
n>>k&1

var n = 211;
var w = n >> 4 & 1;
console.log(w);

控制台会输出：1，即是211二进制表示的第4位数
原理解析：
211： 11010011
>>4 00001101
&1 00000001
re10 ：1

shl，左移运算 <<（二元）

同理，我们的<<运算符则是向左移动，通常可以用来快速进行2的幂运算
这里直接用2的幂运算举例子

var a = 2<<4;
console.log(a);

控制台会输出：32，也就是2的4+1次幂，为什么是4+1？
原理同>>,下面具体化一下：
02：_0000_10
<<4
32：100000

无符号右移（二元）

无符号右移在C中并不存在，在C中对无符号数进行右移便是无符号右移！
（在其他支持语言中大多为>>>）
无符号右移是将二进制数所有位向右移动指定位数，与右移不同，无符号右移空位永远补0。
例如：0b10011 >>> 2 = 0b00100[11]（括号中的数是被裁掉的数）。

参考

空梦的博客
C语言中文网
CSDN

鸣谢

绝大部分内容由：
空梦：https://blog.emptydreams.xyz/binary/提供

啊哈 C 语言

二进制，位以及位运算

什么是二进制？

进制的转换

不同进制在代码中的表示方法

表示方法

在C语言中，我们支持进制输入和输出

下面来详细说说(注意：以下内容仅做扩展阅读)

输出时加上前缀

数字运算

运算： 111101

补码的优点

位运算

&（and,和运算,二元）

|（or,或运算，二元）

xor，异或运算 ^（二元）

not，非运算 ~（一元）

shr，右移运算 >>（二元）

shl，左移运算 <<（二元）

无符号右移（二元）

参考

鸣谢

二进制，位以及位运算

什么是二进制？

进制的转换

不同进制在代码中的表示方法

表示方法

在C语言中，我们支持进制输入和输出

下面来详细说说(注意：以下内容仅做扩展阅读)

输出时加上前缀

数字运算

运算： 111101

补码的优点

位运算

&（and,和 运算,二元）

|（or,或 运算，二元）

xor，异或 运算 ^（二元）

not，非 运算 ~（一元）

shr，右移 运算 >>（二元）

shl，左移 运算 <<（二元）

无符号右移（二元）

参考

鸣谢

&（and,和运算,二元）

|（or,或运算，二元）

xor，异或运算 ^（二元）

not，非运算 ~（一元）

shr，右移运算 >>（二元）

shl，左移运算 <<（二元）