树

二叉搜索树（又称二叉查找树或二叉排序树）：

  1. 若任意结点的左子树不空，则左子树上所有结点的值均不大于它的根结点的值。
  2. 若任意结点的右子树不空，则右子树上所有结点的值均不小于它的根结点的值。
  3. 任意结点的左、右子树也分别为二叉搜索树。

平衡树(Balance Tree，BT)

  1. 指的是，任意节点的子树的高度差都小于等于1。

AVL树的定义

AVL树 是最早被发明的 自平衡二叉查找树

平衡因子 : 树中某结点其左子树的高度和右子树的高度之差
AVL树中的任意一个结点, 其平衡因子的绝对值小于2
AVL树是一种特殊的二叉搜索树 (BST树), 相对于数据极端情况下, 二叉搜索树会退化成为单链表, AVL树定义了旋转操作, 在平衡因子大于等于2时, AVL树会旋转来调整树的结构, 来重新满足平衡因子小于2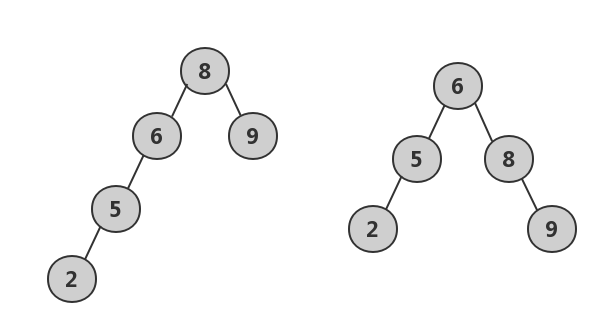
image.png
这两棵树, 右边的为AVL树
现在定义AVL树结构如下:

  1. struct AVLNode 
  2. {
  3.     AVLNode() 
  4.         : val(0), left(nullptr), right(nullptr) 
  5.     {}
  6.     AVLNode(int v)
  7.         : val(v), left(nullptr), right(nullptr)
  8.     {}
  9.     int val;    //data
  10.     // int height;  //当前结点高度
  11.     AVLNode* left;
  12.     AVLNode* right;
  13. };

AVL树不平衡的情况

AVL树大部分操作都和BST树相同, 只有在插入删除结点时, 有可能造成AVL树失去平衡, 而且只有那些在被插入/删除结点到根节点的路径上的结点有可能出现失衡, 因为只有那些结点的子树结构发生了变化
当插入新结点导致不平衡时, 我们需要找到距离新节点最近的不平衡结点为轴来转动AVL树来达到平衡

左子树的左子树插入结点 (左左)

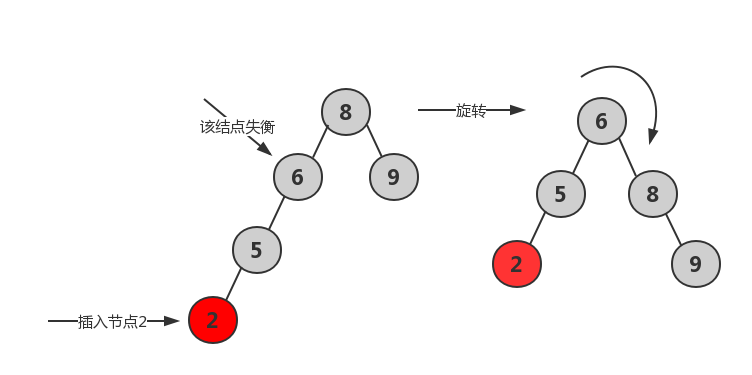
image.png
向该AVL树添加结点 1, 导致结点 6 失衡 ( 结点 2 相对于结点 6 为左子树的左子树), 那么就旋转结点 6, 使其平衡因子重新满足AVL树条件

  1. //左左情况旋转(t是失衡结点)
  2.     void LL(AVLNode** t) 
  3.     {
  4.         if (t != nullptr)
  5.         {
  6.             AVLNode* tmpPtr = (*t)->left;
  7.             (*t)->left = tmpPtr->right;    //t左子树的右子树作为t的左子树
  8.             tmpPtr->right = *t;
  9.             *t = tmpPtr;
  10.         }
  11.     }

右子树的右子树插入节点 (右右)

image.png

  1.  //右右情况旋转
  2.     void RR(AVLNode** t)
  3.     {
  4.         if (t != nullptr) 
  5.         {
  6.             AVLNode* tmpPtr = (*t)->right;
  7.             (*t)->right = tmpPtr->left;
  8.             tmpPtr->left = *t;
  9.             *t = tmpPtr;
  10.         }
  11.     }

左子树的右子树插入节点 (左右)

image.png
结点 8 的左子树的右子树位置插入结点 6, 结点 8 失衡, 这时需要先将失衡节点 8 的左子树进行”右右”情况旋转, 然后再对结点 8 进行”左左”情况旋转

  1. //左右情况旋转 (t为失衡结点,新节点位于t的左子树的右子树)
  2.     void LR(AVLNode** t) 
  3.     {
  4.         RR(&(*t)->left);
  5.         LL(t);
  6.     }

右子树的左子树插入节点 (右左)

image.png
插入结点 12 时失衡, 失衡结点 10 结点, 新结点是其右子树的右子树, 这时需要先将其右子树按”左左”情况向右旋转, 再按”右右”情况向左先旋转

  1. //右左情况旋转
  2.     void RL(AVLNode** t) 
  3.     {
  4.         LL(&(*t)->right);
  5.         RR(t);
  6.     }

删除结点

AVL树是一种特殊的二叉搜索树, 所以要考虑的情况和BST树删除结点一样, 不同的是删除一个结点有可能引起父结点失衡, 所以我们需要在每次回退的时候计算结点高度

  1. //找到左子树中最大值结点
  2. int findMaxKeyInLef(AVLNode* node) 
  3.     {
  4.         if (node == nullptr)
  5.             return 0;
  6.         else if (node->right == nullptr)
  7.             return node->val;
  8.         return findMaxKeyInLef(node->right);
  9.     }
  10.     AVLNode* delNodeFromTree(AVLNode** node, int val) 
  11.     {
  12.         if (node == nullptr) 
  13.             return nullptr;
  14.         else if (val < (*node)->val)
  15.         {
  16.             (*node)->left = delNodeFromTree(&(*node)->left, val);
  17.             //判断是否失衡,删了左子树一个结点,所以判断右子树高度是否过高
  18.             if ((getHeight((*node)->right) - getHeight((*node)->left)) > 1) 
  19.                 //右子树的左子树高度比右子树的右子树更高,相当于给右子树的右子树插入了新节点,相当于"右右"情况
  20.                 if (getHeight((*node)->right->left) > getHeight((*node)->right->right))
  21.                     RL(node);
  22.                 else 
  23.                     RR(node);
  24.             return (*node);
  25.         }
  26.         else if (val > (*node)->val)
  27.         {
  28.             (*node)->right = delNodeFromTree(&(*node)->right, val);
  29.             //判断是否失衡,删了右子树一个结点,所以判断左子树高度是否过高
  30.             if ((getHeight((*node)->left) - getHeight((*node)->right)) > 1) 
  31.                 //左子树的左子树高度比右子树的右子树更高,相当于给左子树的左子树插入了新节点,相当于"左左"情况
  32.                 if (getHeight((*node)->left->left) > getHeight((*node)->left->right))
  33.                     LL(node);
  34.                 else 
  35.                     LR(node);
  36.             return (*node);
  37.         }
  38.         else if (val == (*node)->val)
  39.         {
  40.             //如果是叶子节点
  41.             if ((*node)->left == nullptr && (*node)->right == nullptr) 
  42.             {
  43.                 delete (*node);
  44.                 (*node) = nullptr;
  45.                 return (*node);;
  46.             }
  47.             //如果左子树非空,将右子树续接到父节点
  48.             else if ((*node)->left != nullptr) 
  49.             {
  50.                 AVLNode* tmp = (*node)->left;
  51.                 delete (*node);
  52.                 return tmp;
  53.             }
  54.             //如果右子树非空,将左子树续接到父节点
  55.             else if ((*node)->right != nullptr) 
  56.             {
  57.                 AVLNode* tmp = (*node)->right;
  58.                 delete (*node);
  59.                 return tmp;
  60.             }
  61.             //左右子树皆非空
  62.             else 
  63.             {
  64.                 //寻找左子树中最大节点,即左子树中最右节点
  65.                 //(也可以寻找右子树中最小节点,即右子树中最左节点)
  66.                 int maxVal = findMaxKeyInLef((*node)->left);
  67.                 //交换这两个节点
  68.                 (*node)->val = maxVal;
  69.                 //删除那个用来交换的节点
  70.                 (*node)->left = delNodeFromTree(&(*node)->left, maxVal);
  71.                 return *node;
  72.             }
  73.         }
  74.     }

插入节点

  1.  //插入结点
  2.     void insertNode(AVLNode** t, int v) 
  3.     {   
  4.         //插入结点,使用二级指针改变父节点左右子树指针指向
  5.         if (*t == nullptr) 
  6.             *t = new AVLNode(v); 
  7.         else if (v < (*t)->val) 
  8.         {
  9.             insertNode(&((*t)->left), v);
  10.             int leftH = getHeight((*t)->left);
  11.             int rightH = getHeight((*t)->right);
  12.             //插入到左子树,肯定是左子树高度更高,判断这时平衡因子是否大于1
  13.             if ((leftH - rightH) > 1) 
  14.             {
  15.                 if (v < (*t)->left->val) 
  16.                     LL(t);
  17.                 else
  18.                     LR(t);
  19.             }
  20.         }
  21.         else if (v > (*t)->val) 
  22.         {
  23.             insertNode(&((*t)->right), v);
  24.             int leftH = getHeight((*t)->left);
  25.             int rightH = getHeight((*t)->right);
  26.             if ((rightH - leftH) > 1) 
  27.             {
  28.                 if (v > (*t)->right->val)
  29.                     RR(t);
  30.                 else 
  31.                     RL(t);
  32.             }
  33.         }
  34.         else 
  35.             return ;
  36.     }

更复杂的情况

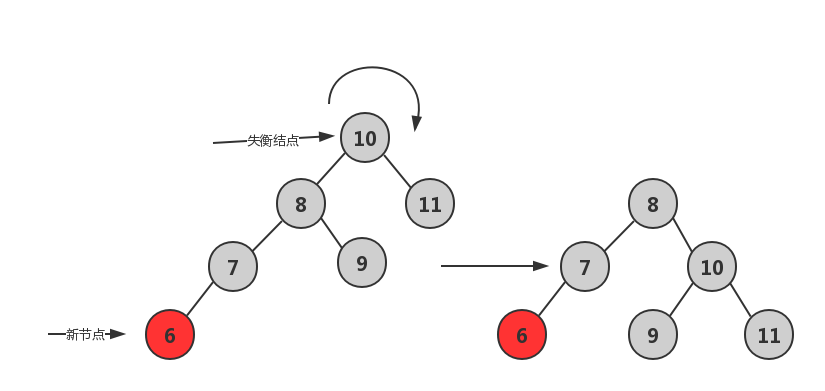
image.png
当我们插入结点 6, 结点 10 失衡, 但第一眼看上去这是”左左左” ? 难道无法处理这种情况吗?
其实这时我们上面给出的”左左”情况下旋转的代码中:

  1.   (*t)->left = tmpPtr->right;    //t左子树的右子树作为t的左子树

就发挥了作用了