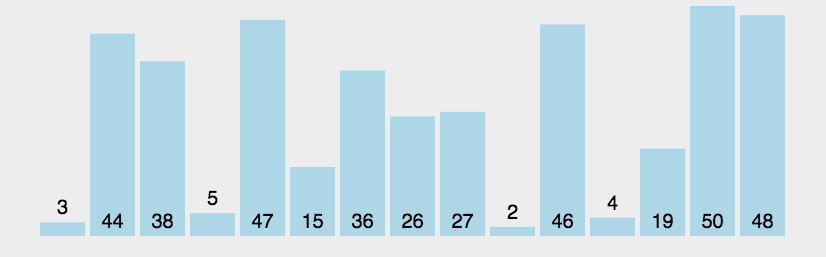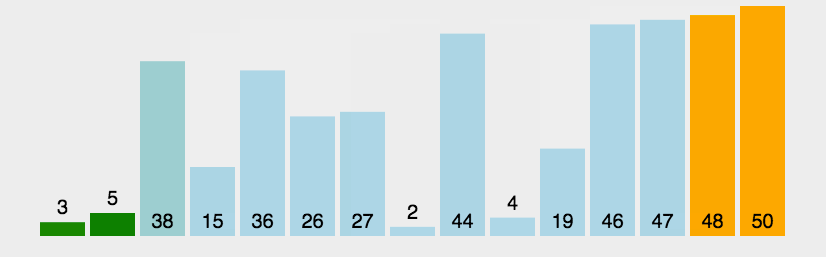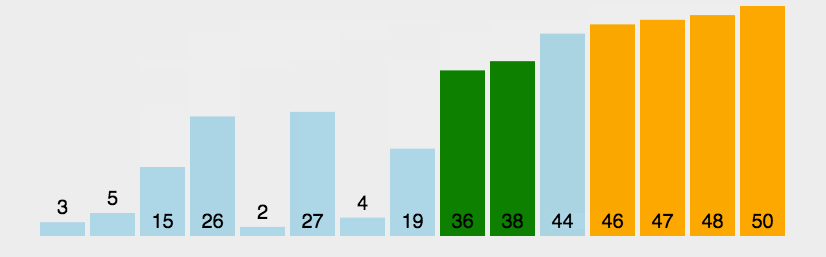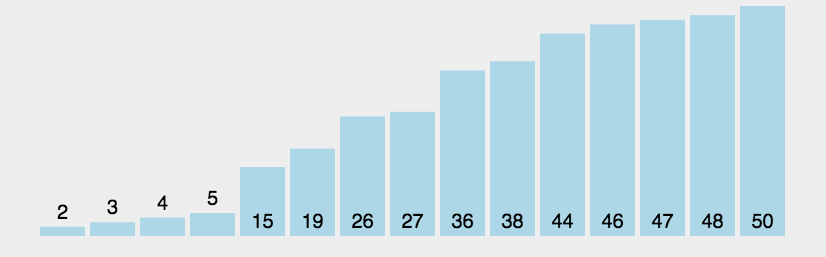| 排序算法 |
平均时间复杂度 |
最好情况 |
最坏情况 |
空间复杂度 |
排序方式 |
稳定性 |
| 冒泡算法 |
O(n2) |
O(n) |
O(n2) |
O(1) |
In-placee |
稳定 |
| 选择排序 |
O(n2) |
O(n2) |
O(n2) |
O(1) |
In-placee |
不稳定 |
| 插入排序 |
O(n2) |
O(n) |
O(n2) |
O(1) |
In-placee |
稳定 |
| 希尔排序 |
O(n log n) |
O(n log2 n) |
O(n log2 n) |
O(1) |
In-placee |
不稳定 |
| 归并排序 |
O(n log n) |
O(n log n) |
O(n log n) |
O(n) |
Out-placee |
稳定 |
| 快速排序 |
O(n log n) |
O(n log n) |
O(n2) |
O(log n) |
In-placee |
不稳定 |
| 堆排序 |
O(n log n) |
O(n log |
O(n log n) |
O(1) |
In-placee |
不稳定 |
| 计数排序 |
O(n + k) |
O(n + k) |
O(n + k) |
O(k) |
Out-placee |
稳定 |
| 桶排序 |
O(n + k) |
O(n + k) |
O(n2) |
O(n + k) |
Out-placee |
稳定 |
| 基数排序 |
O(n × k) |
O(n × k) |
O(n × k) |
O(n + k) |
Out-placee |
稳定 |
一、冒泡排序
1. 代码实现
function BubbleSort(arr) { // 缓存数组长度 const len = arr.length; // 外层循环用于控制从头到尾的比较+交换到底有多少轮 for (let i = 0; i < len - 1; i++) { // 内层循环用于完成每一轮遍历过程中的重复比较+交换 for (let j = 0; j < len - 1 - i; j++) { // 若相邻元素前面的数比后面的大 if (arr[j] > arr[j + 1]) { // 交换两者(方案1) [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]]; // 交换两者(方案2) // var temp = arr[j]; // arr[j] = arr[j+1]; // arr[j+1] = temp; } } } // 返回数组 return arr;}
2. 动画演示
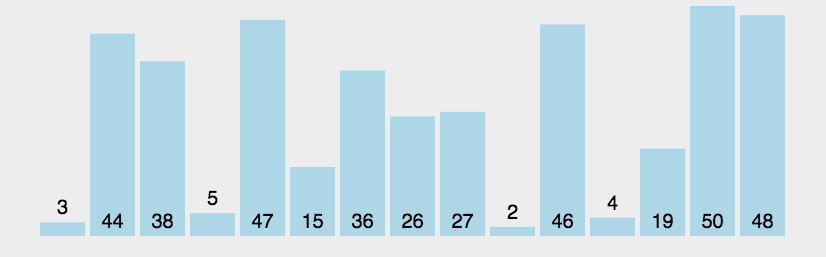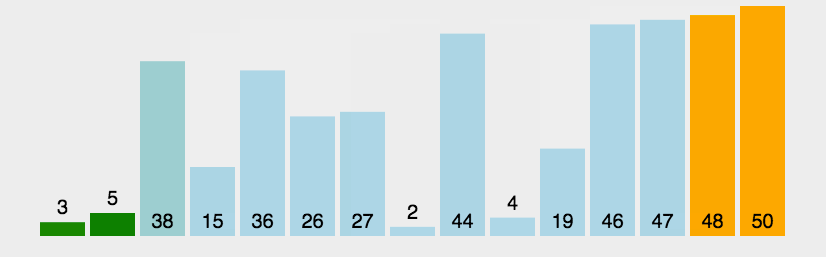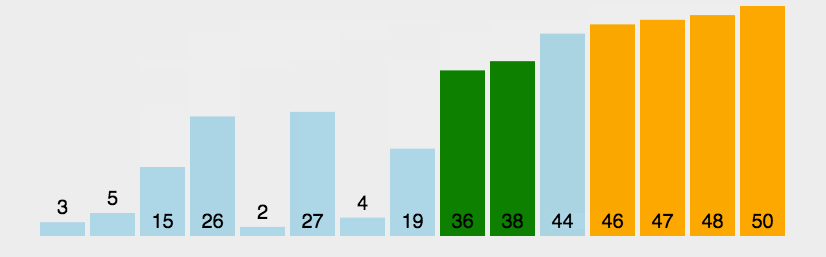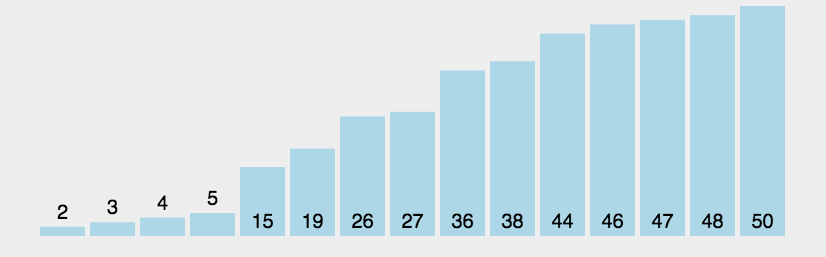
二、选择排序
function SelectionSort(){}
参考链接