图解从武侠角度探究STL排序算法的奥秘

前言

今天来看一下STL中的sort算法的底层实现和代码技巧。

众所周知STL是借助于模板化来支撑数据结构和算法的通用化，通用化对于C++使用者来说已经很惊喜了，但是如果你看看STL开发者强大的阵容就意识到STL给我们带来的惊喜绝不会止步于通用化，强悍的性能和效率是STL的更让人惊艳的地方。

STL极致表现的背后是大牛们炉火纯青的编程技艺和追求极致的工匠精神的切实体现。

笔者能力所限，只能踏着前人的肩膀来和大家一起看看STL中sort算法的背后究竟隐藏着什么，是不是有种《走进科学》的既视感，让我们开始今天的sort算法旅程吧！

内省式哲学

在了解sort算法的实现之前先来看一个概念：内省式排序，说实话笔者的语文水平确实一般，对于这个词语用在排序算法上总觉得不通透，那就研究一下吧！

内省式排序英文是Introspective Sort，其中单词introspective是内省型的意思，还是不太明白，继续搜索，看一下百度百科对这个词条的解释：

内省（Introspection ）在心理学中，它是心理学基本研究方法之一。内省法又称自我观察法。它是发生在内部的，我们自己能够意识到的主观现象。也可以说是对于自己的主观经验及其变化的观察。

正因为它的主观性，内省法自古以来就成为心理学界长期的争论。另外内省也可看作自我反省，也是儒家强调的自我思考。从这个角度说可以应用于计算机领域，如Java内省机制和cocoa内省机制。

好家伙，原来内省是个心理学名词，到这里笔者有些感觉了，内省就是自省、自我思考、根据自己的主观经验来观察变化做出调整，而不是把希望寄托于外界，而是自己的经验和能力。

通俗点说，内省算法不挑数据集，尽量针对每种数据集都能给定对应的处理方法，让排序都能有时间保证。

写到这里，让笔者脑海浮现了《倚天屠龙记》里面张无忌光明顶大战六大门派的场景，无论敌人多么强悍或者羸弱，我都按照自己的路子应对。

他强由他强，清风拂山岗；
他横由他横，明月照大江；
他自狠来他自恶，我自一口真气足。
—-《九阳真经》达摩

哲学啊，确实这样的，我们切换到排序的角度来看看内省是怎么样的过程。

笔者理解的内省式排序算法就是不依赖于外界数据的好坏多寡，而是根据自己针对每种极端场景下做出相应的判断和决策调整，从而来适应多种数据集合展现出色的性能。

内省式排序

俗话说侠者讲究刀、枪、剑、戟、斧、钺、钩、叉等诸多兵器，这也告诉我们一个道理没有哪种兵器是无敌的，只有在某些场景下的明显优势，这跟软件工程没有银弹是一样的。

回到我们的排序算法上，排序算法也可谓是百花齐放：冒泡排序、选择排序、插入排序、快速排序、堆排序、桶排序等等。

虽然一批老一辈的排序算法是O(n^2)的，优秀的算法可以到达O(nlogn)，但是即使都是nlogn的快速排序和堆排序都有各自的长短之处，插入排序在数据几乎有序的场景下性能可以到达O(n)，有时候我们应该做的不是冲突对比而是融合创新。

内省排序是由David Musser在1997年设计的排序算法。这个排序算法首先从快速排序开始，当递归深度超过一定深度（深度为排序元素数量的对数值）后转为堆排序,David Musser大牛是STL领域响当当的人物。

抛开语境一味地对比孰好孰坏其实都没有意义，内省式排序就是集大成者，为了能让排序算法达到一个综合的优异性能，内省式排序算法结合了快速排序、堆排序、插入排序，并根据当前数据集的特点来选择使用哪种排序算法，让每种算法都展示自己的长处，这种思想确实挺启发人的。

内省排序的排兵布阵

前面提到了内省式排序主要结合了快速排序、堆排序、插入排序，那么不禁要问，这三种排序是怎么排兵布阵的呢？

知己知彼百战不殆，所以先看下三种排序的优缺点吧！

快速排序

在大量数据时无论是有序还是重复，使用优化后的算法大多可以到达O(nlogn)，虽然堆排序也是O(nlogn)但是由于某些原因快速排序会更快一些，当递归过深分割严重不均匀情况出现时会退化为O(n^2)的复杂度，这时性能会打折扣，这也就是快速排序的短处了。

堆排序

堆排序是快速排序的有力竞争者，最大的特点是可以到达O(nlogn)并且复杂度很稳定，并不会像快速排序一样可能退化为O(n^2)，但是堆排序过程中涉及大量堆化调整，并且元素比较是跳着来的对Cache的局部性特征利用不好，以及一些其他的原因导致堆排序比快速排序更慢一点，但是大O复杂度仍然是一个级别的。

插入排序

插入排序的一个特点是就像我们玩纸牌，在梳理手中的牌时，如果已经比较有序了，那么只需要做非常少的调整即可，因此插入排序在数据量不大且近乎有序的情况下复杂度可以降低到O(n)，这一点值得被应用。

优缺点也大致清楚了，所以可以猜想一下内省式排序在实际中是如何调度使这三种排序算法的：

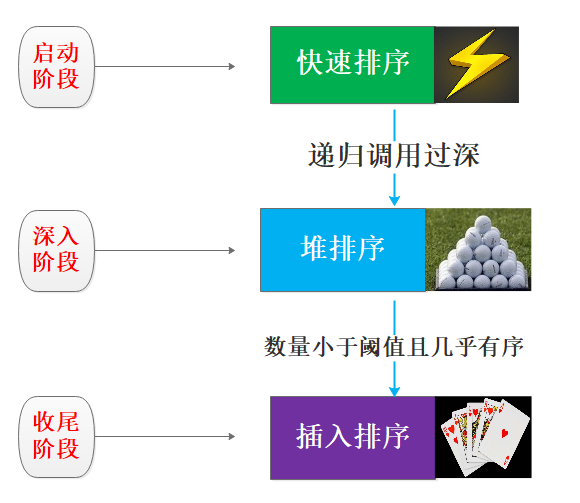
• 启动阶段 面对大量的待排序元素，首先使用快速排序进行大刀阔斧排序，复杂度可以在O(nlogn)运行
• 深入阶段 在快速排序使用递归过程中，涉及栈帧保存切换等诸多递归的操作，如果分区切割不当递归过深可能造成栈溢出程序终止，因此如果快速排序过程中退化为O(n^2)，此时会自动检测切换为堆排序，因为堆排序没有恶化情况，都可以稳定在O(nlogn)
• 收尾阶段 在经过快排和堆排的处理之后，数据分片的待排序元素数量小于某个经验设定值(可以认为是递归即将结束的前几步调用)时，数据其实已经几乎有序，此时就可以使用插入排序来提高效率，将复杂度进一步降低为O(n)。

写到这里，笔者又天马行空地想到了一个场景：

2005年春晚小品中黄宏和巩汉林出演的《装修》中黄宏作为装修工人手拿一大一小两把锤子，大锤80小锤40，大小锤头切换使用。

其实跟内省排序切换排序算法是一个道理，所以技术源于生活又高于生活，贴图一张大家一起体会一下：

用了很多篇幅来讲内省思想和内省式排序，相信大家也已经get到了，所以我们具体看下实现细节，这个才是本文的重点，我们继续往下一起分析吧！

sort算法的实现细节

本文介绍的sort算法是基于SGI STL版本的，并且主要是以侯捷老师的《STL源码剖析》一书为蓝本来进行展开的，因此使用了不带仿函数的版本，让我们来一起领略大牛们的杰作吧！图为笔者买了很久却一直压箱底的STL神书：

sort函数的应用场景

SGI STL中的sort的参数是两个随机存取迭代器RandomAccessIterator，sort的模板也是基于此种迭代器的，因此如果容器不是随机存取迭代器，那么可能无法使用通用的sort函数。

• 关联容器 map和set底层是基于RB-Tree，本身就已经自带顺序了，因此不需要使用sort算法
• 序列容器 list是双向迭代器并不是随机存取迭代器，vector和deque是随机存取迭代器适用于sort算法
• 容器适配器 stack、queue和priority-queue属于限制元素顺序的容器，因此不适用sort算法。

综上我们可以知道，sort算法可以很好的适用于vector和deque这两种容器。

sort总体概览

前面介绍了内省式排序，所以看下sort是怎么一步步来使用introsort的，上一段入口代码：

template <class RandomAccessIterator>
inline void sort(RandomAccessIterator first, RandomAccessIterator last) {
    if (first != last) {
        __introsort_loop(first, last, value_type(first), __lg(last - first) * 2);
        __final_insertion_sort(first, last);
    }
}

从代码来看sort使用了first和last两个随机存取迭代器，作为待排序序列的开始和终止，进一步调用了introsort_loop和final_insertion_sort两个函数，从字面上看前者是内省排序循环，后者是插入排序。其中注意到introsort_loop的第三个参数lg(last - first)*2，凭借我们的经验来猜(蒙)一下吧，应该递归深度的限制，不急看下代码实现：

template <class Size>
inline Size __lg(Size n){
    Size k;
    for(k = 0;n > 1;n >>= 1) ++k;
    return k;
}

这段代码的意思就是n=last-first，2^k<=n的最大整数k值。

所以整体看当假设last-first=20时，k=4,最大分割深度depth_max=4*2=8，从而我们就可以根据first和last来确定递归的最大深度了。

快速排序和堆排序的配合 __introsort_loop函数中主要封装了快速排序和堆排序，来看看这个函数的实现细节：

//sort函数的入口
template <class RandomAccessIterator, class T, class Size>
void __introsort_loop(RandomAccessIterator first,
                      RandomAccessIterator last, T*,
                      Size depth_limit) {
    while (last - first > __stl_threshold) {
        if (depth_limit == 0) {
            partial_sort(first, last, last);//使用堆排序
            return;
        }
        --depth_limit;//减分割余额
        RandomAccessIterator cut = __unguarded_partition
          (first, last, T(__median(*first, *(first + (last - first)/2),
                                   *(last - 1))));//三点中值法分区过程
        __introsort_loop(cut, last, value_type(first), depth_limit);//子序列递归调用
        last = cut;//迭代器交换 切换到左序列
    }
}
//基于三点中值法的分区算法
template <class RandomAccessIterator, class T>
RandomAccessIterator __unguarded_partition(RandomAccessIterator first, 
                                           RandomAccessIterator last, 
                                           T pivot) {
while (true) {
    while (*first < pivot) ++first;
    --last;
    while (pivot < *last) --last;
    if (!(first < last)) return first;
    iter_swap(first, last);
    ++first;
}

各位先不要晕更不要蒙圈，一点点分析肯定可以拿下的。

• 先看参数两个随机存取迭代器first和last，第三个参数是__lg计算得到的分割深度；
• 这时候我们进入了while判断了last-first的区间大小，stl_threshold为16，侯捷大大特别指出stl_threshold的大小可以是5~20，具体大小可以自己设置，如果大于stl_threshold那就才会继续执行，否则跳出；假如现在区间大小大于stl_threshold，判断第三个参数depth_limit是否为0，也就是是否出现了分割过深的情况，相当于给了一个初始最大值，然后每分割一次就减1，直到depth_limit=0，这时候调用partial_sort，从《stl源码剖析》的其他章节可以知道，partial_sort就是对堆排序的封装，看到这里有点意思了主角之一的heapsort出现了；
• 继续往下看，depth_limit>0 尚有分割余额，那就燥起来吧！这样来到了unguarded_partition，这个函数从字眼看是快速排序的partiton过程，返回了cut随机存取迭代器，unguarded_partition的第三个参数__median使用的是三点中值法来获取的基准值Pivot，至此快速排序的partition的三个元素集齐了，最后返回新的切割点位置；
• 继续看马上搞定啦，__introsort_loop出现了，果然递归了，特别注意一下这里只有一个递归，并且传入的是cut和last，相当于右子序列，那左子序列怎么办啊？别急往下看，last=cut峰回路转cut变成了左子序列的右边界，这样就开始了左子序列的处理；

快速排序的实现对比

前面提到了在sort中快速排序的写法和我们之前见到的有一些区别，看了一下《STL源码剖析》对快排左序列的处理，侯捷老师是这么写的：”写法可读性较差，效率并没有比较好”，看到这里更蒙圈了，不过也试着分析一下吧！

图为：STL源码剖析中侯捷老师对该种写法的注释

常见写法：

//快速排序的常见写法伪代码
quicksort(arr,left,right){
    pivoit = func(arr);//使用某种方法获取基准值
    cut = partition(left,right,pivot);//左右边界和基准值来共同确定分割点位置
    quicksort(arr,left,cut-1);//递归处理左序列
    quicksort(arr,cut+1,right);//递归处理右序列
}

SGI STL中的写法:

stl_quicksort(first,last){
      //循环作为外层控制结构
      while(ok){
         cut = stl_partition(first,last,_median(first,last));//分割分区
         stl_quicksort(cut,last);//递归调用 处理右子序列
         last = cut;//cut赋值为last 相当于切换到左子序列 再继续循环
   }
}

网上有一些大佬的文章说sgi stl中快排的写法左序列的调用借助了while循环节省了一半的递归调用，是典型的尾递归优化思路。

这里我暂时还没有写测试代码做对比，先占坑后续写个对比试验，再来评论吧，不过这种sgi的这种写法可以看看哈。

堆排序的细节

//注：这个是带自定义比较函数的堆排序版本
//堆化和堆顶操作
template <class RandomAccessIterator, class T, class Compare>
void __partial_sort(RandomAccessIterator first, RandomAccessIterator middle,
                    RandomAccessIterator last, T*, Compare comp) {
    make_heap(first, middle, comp);
    for (RandomAccessIterator i = middle; i < last; ++i)
        if (comp(*i, *first))
            __pop_heap(first, middle, i, T(*i), comp, distance_type(first));
    sort_heap(first, middle, comp);
}
//堆排序的入口
template <class RandomAccessIterator, class Compare>
inline void partial_sort(RandomAccessIterator first,
                         RandomAccessIterator middle,
                         RandomAccessIterator last, Compare comp) {
    __partial_sort(first, middle, last, value_type(first), comp);
}

插入排序上场了

introsort_loop达到stl_threshold阈值之后，可以认为数据集近乎有序了，此时就可以通过插入排序来进一步提高排序速度了，这样也避免了递归带来的系统消耗，看下__final_insertion_sort的具体实现：

template <class RandomAccessIterator>
void __final_insertion_sort(RandomAccessIterator first, 
                            RandomAccessIterator last) {
    if (last - first > __stl_threshold) {
        __insertion_sort(first, first + __stl_threshold);
        __unguarded_insertion_sort(first + __stl_threshold, last);
    }
    else
        __insertion_sort(first, last);
}

来分析一下__final_insertion_sort的实现细节吧:

• 引入参数随机存取迭代器first和last
• 如果last-first > stl_threshold不成立就调用insertion_sort，这个相当于元素数比较少了可以直接调用，不用做特殊处理；
• 如果last-first > stl_threshold成立就进一步再分割成两部分，分别调用insertion_sort和unguarded_insertion_sort，两部分的分割点是stl_threshold，不免要问这俩函数有啥区别呀？

__insertion_sort的实现

//逆序对的调整
template <class RandomAccessIterator, class T>
void __unguarded_linear_insert(RandomAccessIterator last, T value) {
    RandomAccessIterator next = last;
    --next;
    while (value < *next) {
        *last = *next;
        last = next;
        --next;
    }
    *last = value;
}
template <class RandomAccessIterator, class T>
inline void __linear_insert(RandomAccessIterator first, 
                            RandomAccessIterator last, T*) {
    T value = *last;
    if (value < *first) {
        copy_backward(first, last, last + 1);//区间移动
        *first = value;
    }
    else
        __unguarded_linear_insert(last, value);
}
//__insertion_sort入口
template <class RandomAccessIterator>
void __insertion_sort(RandomAccessIterator first, RandomAccessIterator last) {
    if (first == last) return; 
    for (RandomAccessIterator i = first + 1; i != last; ++i)
        __linear_insert(first, i, value_type(first));
}

在插入函数中同样出现了__unguarded_xxx这种形式的函数，unguarded单词的意思是无防备的，无保护的，侯捷大大提到这种函数形式是特定条件下免去边界检验条件也能正确运行的函数。

copy_backward也是一种整体移动的优化，避免了one by one的调整移动，底层调用memmove来高效实现。

__unguarded_insertion_sort的实现

template <class RandomAccessIterator, class T>
void __unguarded_insertion_sort_aux(RandomAccessIterator first, 
                                    RandomAccessIterator last, T*) {
    for (RandomAccessIterator i = first; i != last; ++i)
        __unguarded_linear_insert(i, T(*i));
}
template <class RandomAccessIterator>
inline void __unguarded_insertion_sort(RandomAccessIterator first, 
                                RandomAccessIterator last) {
    __unguarded_insertion_sort_aux(first, last, value_type(first));
}

关于插入排序的这两个函数的实现和目的用途，展开起来会很细致，所以后面想着单独在写插入排序时单独拿出了详细学习一下，所以本文就暂时先不深究了，感兴趣的读者可以先行阅读相关资料，后续我们再共同辩驳哈！

总结

本文主要阐述了内省式排序的思想和基本实现思路，并且以此为切入点对sgi stl中sort算法的实现来进行了一些解读。

stl的作者们为了追求极致性能所以使用了大量的技巧，对此本文并没有过多展开，也主要是段位不太高怕解读错了，聪明的读者们可以尝试来剖析一探大牛们的巅峰技艺。