关系代数是—种抽象的查询语言，用对关系的运算来表达查询，作为研究关系数据语言的数学工具。个人认为屁用没有，纯纯为了考试而学。

    关系代数包含两类运算：关系运算的运算对象是关系，运算结果也是关系。

    • 传统的集合运算：如并、交、差、笛卡儿积，这类运算将关系看成元组的集合，其运算是从关系的“水平”方向、行的角度来进行的。
    • 扩充的关系运算：如选择、投影、连接、除，这类运算不仅涉及行，而且涉及列。
    • 五种基本操作：并、差、笛卡儿积、选择、投影 —->(∪、-、×、σ、Π)
    • 三种组合操作：交、连接、除 —->(∩、⨝、÷)

    image.png

    并(∪)操作：R∪S
    运算结果：至少出现在两个关系中之一的元组的集合。
    运算前提：R和S必须是相容的：

    • 关系R和S必须是同元的，即它们的属性数目必须相同。
    • 对任意正整数i，R的第i个属性和S的第i个属性的数据类型必须相同。

    image.png

    差(—)操作：R—S
    运算结果：是由属于R，但是不属于S的元组构成的集合。
    运算前提：R和S必须同类型（属性集相同，但属性名可以不同)。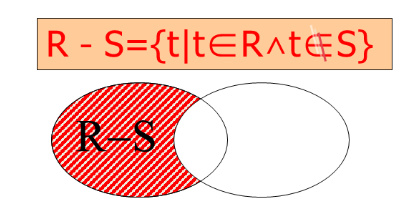
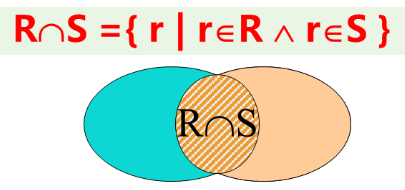
    image.png

    交(∩)操作：R∩S
    运算结果：所有同时出现在两个关系中的元组集合。
    运算前提：

    • 交运算可以通过差运算来实现：R∩S=R-(R-S) 或 S-(S-R)
    • R和S必须同类型（属性集相同、次序相同，属性名可以不同)

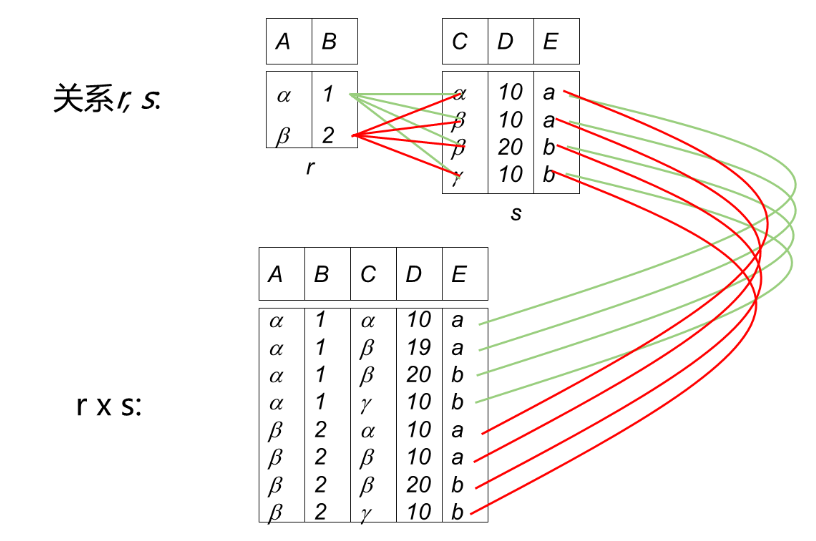
    image.png

    笛卡尔积(×)：R×S
    运算结果：

    • 关系R和S的笛卡儿积是两个关系的元组对的集合所组成的新关系。
    • 关系R×S的字段名可分为两部分，前r个字段名来自R，后s个字段名来自S。
    • 关系R×S的字段数为R和S字段数之和，元组个数为R和S元组数之积。

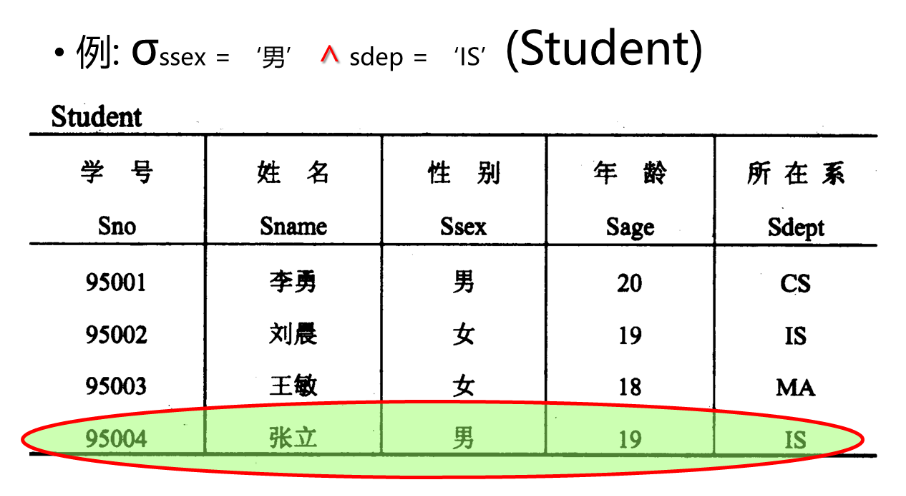
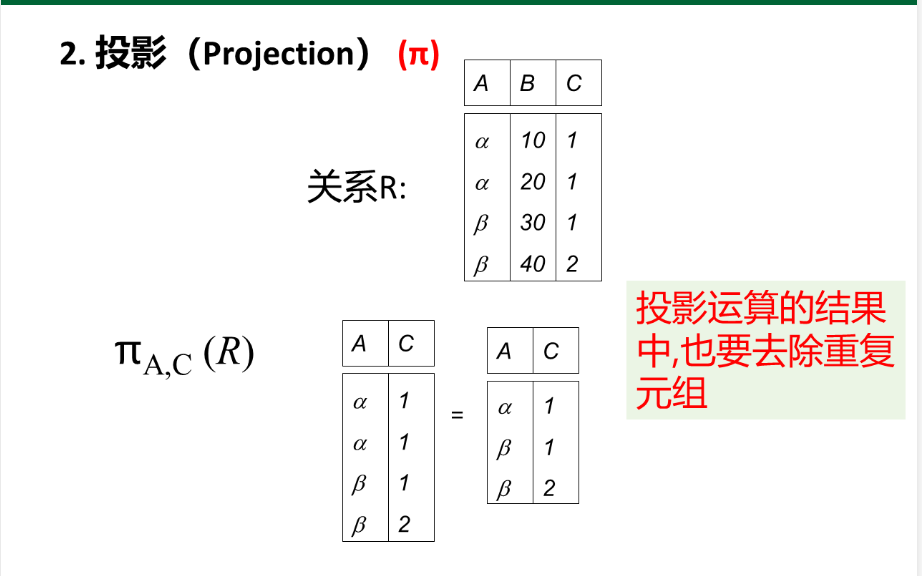
    image.png

    选择(σ)操作：
    image.png
    image.png

    投影(Π)操作：

    • 对一个关系R进行垂直分割，消去某些列，并重新安排列的顺序。
    • ΠA1A2…An(R),表示从R中选择属性集A1,A2…….,An组成新的关系
    • 属于列的运算，投影运算的结果中,也要去除可能的重复元组

    image.png