可以说现在的安全计算方法多是基于两大类基于噪声的和不基于噪声的
- 基于噪声：如现在大火的差分隐私
- 效率比较高，只需要生成一定分布的噪声即可实现隐私保护效果
- 结果不够准确，结果可用性和隐私保护安全性成反比
- 不基于噪声：基于密码学，如安全多方计算
2.拉普拉斯机制和高斯机制详解
作为差分隐私主要实现机制，高斯机制和拉普拉斯机制需要详解和深解✌✌
2.1.Laplace机制
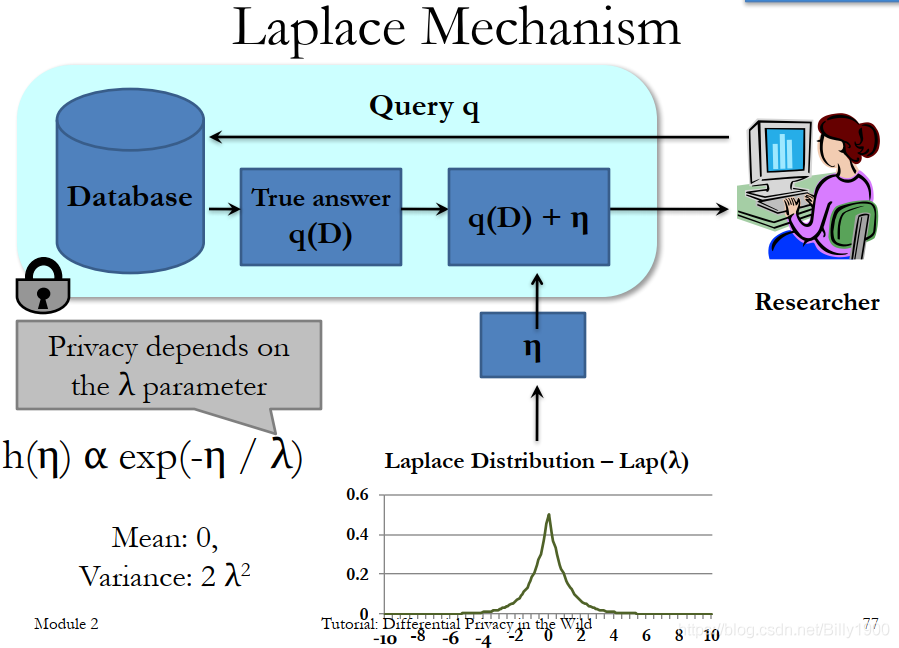
2.1.1.Laplace噪声
laplace噪声函数表达式为：
%3D%5Cfrac%7B1%7D%7B2%5Clambda%7De%5E%7B%5Cfrac%20%7B-%5Cvert%20x%20-%20%5Cmu%20%5Cvert%7D%20%7B%5Clambda%7D%7D%0A#card=math&code=f%28x%20%5Cvert%20%5Cmu%20%2C%20%5Clambda%29%3D%5Cfrac%7B1%7D%7B2%5Clambda%7De%5E%7B%5Cfrac%20%7B-%5Cvert%20x%20-%20%5Cmu%20%5Cvert%7D%20%7B%5Clambda%7D%7D%0A&id=LYVhG)
表示期望，图像上表示对称轴
代表变量
方差表示为
差分隐私中，经常令
等于0，
等于
此时Laplace函数为：
%3D%5Cfrac%20%7B1%7D%20%7B(%5Cfrac%20%7B2%20%5CDelta%20f%7D%20%7B%5Cepsilon%7D)%7De%5E%5Cfrac%7B-%20%5Cvert%20x%20%5Cvert%7D%7B(%5Cfrac%7B%5CDelta%20f%7D%7B%5Cepsilon%7D)%7D%0A#card=math&code=Lap%28%5Cfrac%20%7B%5CDelta%20f%7D%20%7B%5Cepsilon%7D%29%3D%5Cfrac%20%7B1%7D%20%7B%28%5Cfrac%20%7B2%20%5CDelta%20f%7D%20%7B%5Cepsilon%7D%29%7De%5E%5Cfrac%7B-%20%5Cvert%20x%20%5Cvert%7D%7B%28%5Cfrac%7B%5CDelta%20f%7D%7B%5Cepsilon%7D%29%7D%0A&id=bdYdP)
化简可得：
%3D%5Cfrac%7B%5Cepsilon%7D%7B2%20%5CDelta%20f%7De%5E%7B%5Cfrac%20%7B-%5Cepsilon%20%5Cvert%20x%20%5Cvert%7D%20%7B%20%5CDelta%20f%7D%7D%0A#card=math&code=Lap%28%5Cfrac%7B%5CDelta%20f%7D%7B%5Cepsilon%7D%29%3D%5Cfrac%7B%5Cepsilon%7D%7B2%20%5CDelta%20f%7De%5E%7B%5Cfrac%20%7B-%5Cepsilon%20%5Cvert%20x%20%5Cvert%7D%20%7B%20%5CDelta%20f%7D%7D%0A&id=Kfhs7)
在使用Laplace实现差分隐私后，我们对数据库或其他查询客体的查询就相当于上式中的x
2.1.2.Laplace证明
噪声
#card=math&code=Y%20~%20L%280%2C%5Cfrac%7B%5CDelta%20f%7D%7B%5Cepsilon%7D%29&id=WL2Pf)满足
-differential%20%5Cquad%20privacy#card=math&code=%28%5Cepsilon%2C0%29-differential%20%5Cquad%20privacy&id=ww5TX)
证明：
%3DS%5D%7D%7BP%5BM(D%5E%7B’%7D)%3DS%5D%7D%20%0A%20%09%26%20%3D%5Cln%20%5Cfrac%7B%5Cfrac%7B%5Cepsilon%7D%7B2%20%5CDelta%20f%7De%5E%7B%5Cfrac%20%7B-%5Cepsilon%20%5Cvert%20f(D)%20%5Cvert%7D%20%7B%20%5CDelta%20f%7D%7D%7D%7B%5Cfrac%7B%5Cepsilon%7D%7B2%20%5CDelta%20f%7De%5E%7B%5Cfrac%20%7B-%5Cepsilon%20%5Cvert%20f(D%5E%7B’%7D)%20%5Cvert%7D%20%7B%20%5CDelta%20f%7D%7D%7D%20%5C%5C%0A%20%09%26%20%3D%20%5Cfrac%20%7B%5Cepsilon%7D%7B%5CDelta%20f%7D(%7Cf(D)%7C-%7Cf(D%5E%7B’%7D)%7C)%20%5Cleqslant%20%5Cepsilon%0A%20%09%5Cend%7Bsplit%7D%0A%5Cend%7Bequation*%7D%0A#card=math&code=%5Cbegin%7Bequation%2A%7D%0A%20%09%5Cbegin%7Bsplit%7D%0A%20%09%5Cln%20%5Cfrac%7BP%5BM%28D%29%3DS%5D%7D%7BP%5BM%28D%5E%7B%27%7D%29%3DS%5D%7D%20%0A%20%09%26%20%3D%5Cln%20%5Cfrac%7B%5Cfrac%7B%5Cepsilon%7D%7B2%20%5CDelta%20f%7De%5E%7B%5Cfrac%20%7B-%5Cepsilon%20%5Cvert%20f%28D%29%20%5Cvert%7D%20%7B%20%5CDelta%20f%7D%7D%7D%7B%5Cfrac%7B%5Cepsilon%7D%7B2%20%5CDelta%20f%7De%5E%7B%5Cfrac%20%7B-%5Cepsilon%20%5Cvert%20f%28D%5E%7B%27%7D%29%20%5Cvert%7D%20%7B%20%5CDelta%20f%7D%7D%7D%20%5C%5C%0A%20%09%26%20%3D%20%5Cfrac%20%7B%5Cepsilon%7D%7B%5CDelta%20f%7D%28%7Cf%28D%29%7C-%7Cf%28D%5E%7B%27%7D%29%7C%29%20%5Cleqslant%20%5Cepsilon%0A%20%09%5Cend%7Bsplit%7D%0A%5Cend%7Bequation%2A%7D%0A&id=ZR4qG)
因此需要满足：
%7C-%7Cf(D%5E%7B’%7D)%7C%20%5Cleqslant%20%5CDelta%20f%20%5C%5C%0A%09%26%20%7Cf(D)%7C-%7Cf(D%5E%7B’%7D)%7C%20%5Cleqslant%20%5Cmax%7BD%2CD%5E%7B’%7D%7D%7B%7Cf(D)%7C-%7Cf(D%5E%7B’%7D)%7C%7D%0A%09%5Cend%7Bsplit%7D%0A%5Cend%7Bequation*%7D%0A#card=math&code=%5Cbegin%7Bequation%2A%7D%0A%09%5Cbegin%7Bsplit%7D%0A%09%26%20%7Cf%28D%29%7C-%7Cf%28D%5E%7B%27%7D%29%7C%20%5Cleqslant%20%5CDelta%20f%20%5C%5C%0A%09%26%20%7Cf%28D%29%7C-%7Cf%28D%5E%7B%27%7D%29%7C%20%5Cleqslant%20%5Cmax%7BD%2CD%5E%7B%27%7D%7D%7B%7Cf%28D%29%7C-%7Cf%28D%5E%7B%27%7D%29%7C%7D%0A%09%5Cend%7Bsplit%7D%0A%5Cend%7Bequation%2A%7D%0A&id=sRyZ5)
通过观察可知，上式满足绝对不等式，证明。
Laplace机制证明关键在于约束
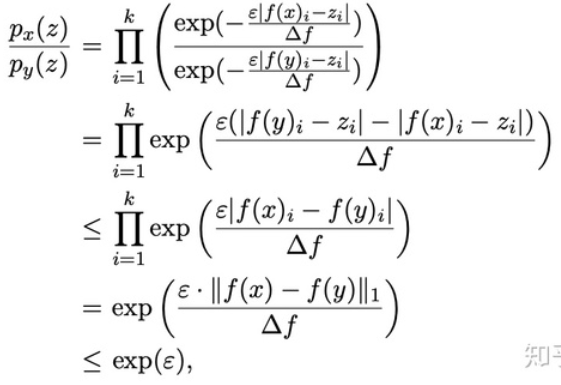
2.1.3.Laplace关键点
Laplace机制提供的是严格的
-DP#card=math&code=%EF%BC%88%5Cepsilon%2C0%29-DP&id=NP0ZV),通常来讲，这在现实应用中是严苛的。在使用Laplace机制时，由于其函数表达式(本质就是噪声的分布形式），我们通常使用
2.2.Gaussian机制
2.2.1.Gaussian噪声
Gaussian噪声表达式为：
%3D%5Cfrac%7B1%7D%7B%5Csqrt%7B2%20%5Cpi%7D%5Csigma%7De%5E%7B-%5Cfrac%7B(x-%5Cmu)%5E2%7D%7B%5Csigma%5E2%7D%7D%0A#card=math&code=f%28x%29%3D%5Cfrac%7B1%7D%7B%5Csqrt%7B2%20%5Cpi%7D%5Csigma%7De%5E%7B-%5Cfrac%7B%28x-%5Cmu%29%5E2%7D%7B%5Csigma%5E2%7D%7D%0A&id=n1LN8)
为期望值
为方差
为变量
2.2.2.Gaussian证明
对于任意的
,有噪声
#card=math&code=Y%20%5Csim%20N%280%2C%5Csigma%5E2%29&id=q2kNa)满足
-DP#card=math&code=%28%5Cepsilon%2C%5Cdelta%29-DP&id=K9364),在使用了搞事机制差分隐私的随机梯度下降算法中，应满足
%20%5Cin%20S%20%5D%20%5Cleqslant%20e%5E%7B%5Cepsilon%7DP%5BM(D%5E%7B’%7D%5Cin%20S)%5D%2B%5Cdelta%0A#card=math&code=P%5BM%28D%29%20%5Cin%20S%20%5D%20%5Cleqslant%20e%5E%7B%5Cepsilon%7DP%5BM%28D%5E%7B%27%7D%5Cin%20S%29%5D%2B%5Cdelta%0A&id=AQD6p)
其中三个参数分别代表
高斯分布标准差
，决定了噪声尺度
表示隐私预算，和噪声成负相关
表示松驰项，比如设置为
，就表示只能容忍
的概率违反严格差分隐私
- 在松弛差分隐私中，输出为两部分，一部分严格遵守DP，另一部分违反DP。
- 需要分别证明第一部分被
约束，另一部分小于
。
这里用
表示这遵守严格差分隐私的，
表示这违反严格差分隐私的部分
%7D%5Bf(x)%2Bx%20%5Cin%20S%5D%20%5C%5C%0A%09%26%20%3D%20%5CPr%20%5Climits%7Bx%20%5Csim%20N(0%2C%5Csigma%5E2)%7D%5Bf(x)%2Bx%20%5Cin%20S_1%5D%2B%5CPr%20%5Climits%7Bx%20%5Csim%20N(0%2C%5Csigma%5E2)%7D%5Bf(x)%2Bx%20%5Cin%20S2%5D%20%5C%5C%0A%09%26%20%5Cleq%20%5CPr%20%5Climits%7Bx%20%5Csim%20N(0%2C%5Csigma%5E2)%7D%5Bf(x)%2Bx%20%5Cin%20S1%5D%2B%5Cdelta%20%5C%5C%0A%09%26%20%5Cleq%20e%5E%7B%5Cepsilon%7D(%5CPr%20%5Climits%7Bx%20%5Csim%20N(0%2C%5Csigma%5E2)%7D%5Bf(x)%2Bx%20%5Cin%20S1%5D%2B%5Cdelta)%0A%09%5Cend%7Bsplit%7D%0A%5Cend%7Bequation*%7D%0A#card=math&code=%5Cbegin%7Bequation%2A%7D%0A%09%5Cbegin%7Bsplit%7D%0A%09%26%20%5CPr%20%5Climits%7Bx%20%5Csim%20N%280%2C%5Csigma%5E2%29%7D%5Bf%28x%29%2Bx%20%5Cin%20S%5D%20%5C%5C%0A%09%26%20%3D%20%5CPr%20%5Climits%7Bx%20%5Csim%20N%280%2C%5Csigma%5E2%29%7D%5Bf%28x%29%2Bx%20%5Cin%20S_1%5D%2B%5CPr%20%5Climits%7Bx%20%5Csim%20N%280%2C%5Csigma%5E2%29%7D%5Bf%28x%29%2Bx%20%5Cin%20S2%5D%20%5C%5C%0A%09%26%20%5Cleq%20%5CPr%20%5Climits%7Bx%20%5Csim%20N%280%2C%5Csigma%5E2%29%7D%5Bf%28x%29%2Bx%20%5Cin%20S1%5D%2B%5Cdelta%20%5C%5C%0A%09%26%20%5Cleq%20e%5E%7B%5Cepsilon%7D%28%5CPr%20%5Climits%7Bx%20%5Csim%20N%280%2C%5Csigma%5E2%29%7D%5Bf%28x%29%2Bx%20%5Cin%20S_1%5D%2B%5Cdelta%29%0A%09%5Cend%7Bsplit%7D%0A%5Cend%7Bequation%2A%7D%0A&id=vW35L)
2.2.3.Gaussian关键点
Gaussian机制提供的是松弛的差分隐私，这个也是经常被应用到现实场景中的实现机制，鉴于Gaussian噪声的分布，Gaussian采用
，高斯机制比较难，需要进一步深入了解。
3.为什么使用Gaussian机制呢？
