优先队列的实现比较
| 实现 | 插入 | 删除 | 查找最大/最小关键字 | 缺点 |
|---|---|---|---|---|
| 数组 | 1 | n | n | - |
| 链表 | 1 | n | 1 | - |
| 有序数组 | n 或 logn | n | 1 | - |
| 有序链表 | n | 1 | 1 | - |
| 二叉搜索树 | logn | logn | logn | 多次删除后容易导致树倾斜 |
| 二叉堆 | logn | logn | 1 |
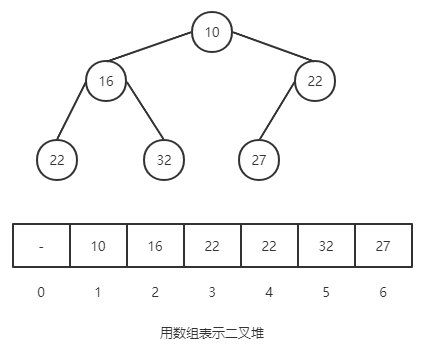
二叉堆
二叉堆的性质
- 节点 k 的父节点下标为 k / 2(向下取整)
- 已某节点为根节点的子树,该节点是这颗树的极值
二叉堆的操作
插入
二叉堆的插入非常简单,只需要在二叉堆的最后添加要插入的内容,并将其“上浮”到正确位置。
尝试在上面的二叉堆中插入新元素9,过程如下:
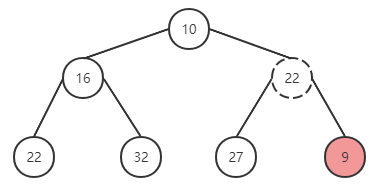
在尾部插入元素9,与父节点进行对比,有序性被破坏,与父元素替换位置。
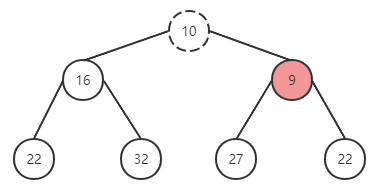
替换成功后,继续上一轮操作,与父节点进行对比,仍然无法满足有序性,继续调换位置。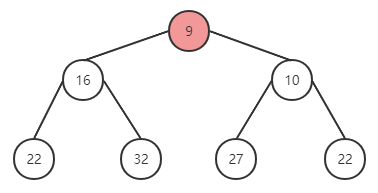
实现
function push(heap: Heap, node: Node): void {const index = heap.length;heap.push(node); // 在堆尾部添加元素siftUp(heap, node, index); // 进行上浮操作}function siftUp(heap, node, i) {let index = i;while (true) {const parentIndex = (index - 1) >>> 1; // 父节点位置: parentIndex = childIndex / 2const parent = heap[parentIndex];if (parent !== undefined && compare(parent, node) > 0) {// The parent is larger. Swap positions.heap[parentIndex] = node;heap[index] = parent;index = parentIndex;} else {// The parent is smaller. Exit.return;}}}
删除
取出根节点的值对比插入稍微复杂一点,归纳起来可以分为三步:
- 取出根节点的值。
- 将最后一个元素与根节点进行替换,并删除最后一个元素。
- 下沉;
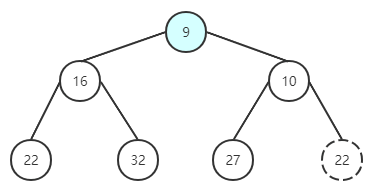
取出根节点。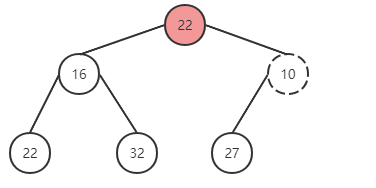
将最后一个元素与根节点调换,并删除。对比发现有序性被破坏,进行对调。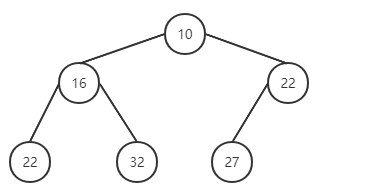
完成删除。
程序框架
function pop {* 设定 minItem 保存根节点* 取出最后一个节点与根节点替换,并删除最后一个节点* 执行下沉循环* 将根元素与左右子节点对比,挑选较小的与父节点替换位置return minItem}
实现
export function pop(heap: Heap): Node | null {const first = heap[0]; // 取出根节点if (first !== undefined) {const last = heap.pop(); // 取出最后一位元素,并删除if (last !== first) {heap[0] = last; // 与根节点对调siftDown(heap, last, 0); // 下沉}return first;} else {return null;}}function siftDown(heap, node, i) {let index = i;const length = heap.length;while (index < length) {const leftIndex = (index + 1) * 2 - 1;const left = heap[leftIndex];const rightIndex = leftIndex + 1;const right = heap[rightIndex];// If the left or right node is smaller, swap with the smaller of those.// 寻找左右儿子较小的那一个替换if (left !== undefined && compare(left, node) < 0) { //左子节点小于根节点if (right !== undefined && compare(right, left) < 0) {heap[index] = right;heap[rightIndex] = node;index = rightIndex;} else {heap[index] = left;heap[leftIndex] = node;index = leftIndex;}} else if (right !== undefined && compare(right, node) < 0) { // 左子接点大于根节点,右子节点小于根节点heap[index] = right;heap[rightIndex] = node;index = rightIndex;} else {// Neither child is smaller. Exit.return;}}}
以下是 react 源码中 scheduler/src/SchedulerMinHeap.js 关于最小堆的完整实现:
/*** Copyright (c) Facebook, Inc. and its affiliates.** This source code is licensed under the MIT license found in the* LICENSE file in the root directory of this source tree.** @flow strict*/type Heap = Array<Node>;type Node = {|id: number,sortIndex: number,|};export function push(heap: Heap, node: Node): void {const index = heap.length;heap.push(node);siftUp(heap, node, index);}export function peek(heap: Heap): Node | null {const first = heap[0];return first === undefined ? null : first;}export function pop(heap: Heap): Node | null {const first = heap[0];if (first !== undefined) {const last = heap.pop();if (last !== first) {heap[0] = last;siftDown(heap, last, 0);}return first;} else {return null;}}function siftUp(heap, node, i) {let index = i;while (true) {const parentIndex = (index - 1) >>> 1; // 父节点位置: parentIndex = childIndex / 2const parent = heap[parentIndex];if (parent !== undefined && compare(parent, node) > 0) {// The parent is larger. Swap positions.heap[parentIndex] = node;heap[index] = parent;index = parentIndex;} else {// The parent is smaller. Exit.return;}}}function siftDown(heap, node, i) {let index = i;const length = heap.length;while (index < length) {const leftIndex = (index + 1) * 2 - 1;const left = heap[leftIndex];const rightIndex = leftIndex + 1;const right = heap[rightIndex];// If the left or right node is smaller, swap with the smaller of those.if (left !== undefined && compare(left, node) < 0) { //if (right !== undefined && compare(right, left) < 0) {heap[index] = right;heap[rightIndex] = node;index = rightIndex;} else {heap[index] = left;heap[leftIndex] = node;index = leftIndex;}} else if (right !== undefined && compare(right, node) < 0) {heap[index] = right;heap[rightIndex] = node;index = rightIndex;} else {// Neither child is smaller. Exit.return;}}}function compare(a, b) {// Compare sort index first, then task id.const diff = a.sortIndex - b.sortIndex;return diff !== 0 ? diff : a.id - b.id;}