4、排序

4.1 插入排序

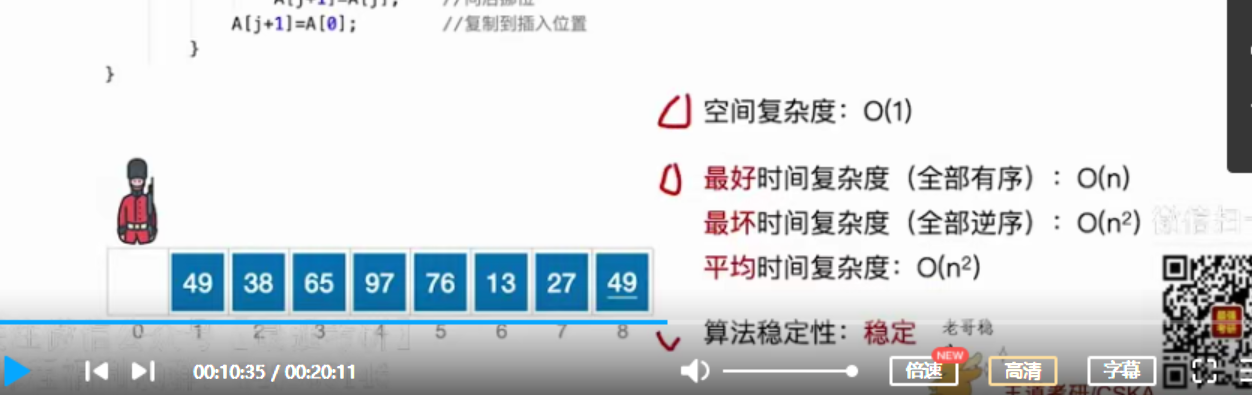
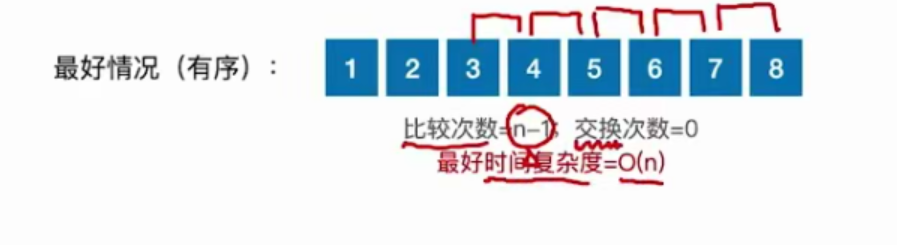
4.1.1 直接插入排序

//不带哨兵，能基于顺序表和链表
void InsertSort(int A[],int n){
    int i,j,temp;
    for(i=1;i<n;i++)
        if(A[i]<A[i-1]){
            temp=A[i];
            for(j=i-1;j>=0 && A[j]>temp;j--)
                A[j+1]=A[j];
            A[j+1]=temp;
        }
}
//带哨兵
void InsertSort(int A[],int n){
    int i,j;
    for(i=2;i<=n;i++)
        if(A[i]<A[i-1]){
            A[0]=A[i];
            for(j=i-1;A[j]>A[0];j--)
                A[j+1]=A[j];
            A[j+1]=A[0];
        }
}

算法效率

4.1.2 折半插入排序

//折半插入排序，只能基于顺序表
void InsertSort(int A[],int n){
    int i,j,low,high,mid;
    for(i=2;i<=n;i++){
        A[0]=A[i];
        low=1;
        high=i-1;
        while(low<=high){
            mid=(low+high)/2;
            if(A[mid]>A[0])
                high=mid-1;
            else
                low=mid+1;
        }
        for(j=i-1;j>=high+1;j--)
            A[j+1]=A[j];
        A[high+1]=A[0];
    }
}

4.1.3 希尔排序（Shell Sort）

//希尔排序，只能基于顺序表
void ShellSort(int A[],int n){
    int d,i,j;
    for(d=n/2;d>=1;d=d/2)
        for(i=d+1;i<=n;++i)
            if(A[i]<A[i-d]){
                A[0]=A[i];
                for(j=i-d;j>0 && A[0]<A[j];j-=d)
                    A[j+d]=A[j];
                A[j+d]=A[0];
            }
}

总结：直接插入、折半插入是稳定的
希尔排序是不稳定的

4.2 交换排序

4.2.1 冒泡排序

//适用于链表和顺序表    
void BubbleSort(int A[],int n){
        for(int i=0;i<n-1;i++){
            Boolean flag=false;
            for(int j=1;j<n-i;j++){
                if(A[j-1]>A[j]){
                    int temp=A[j];
                    A[j]=A[j-1];
                    A[j-1]=temp;
                    flag=true;
                }
            }
            if(flag==false)
                return ;
        }
    }

冒泡排序是稳定的

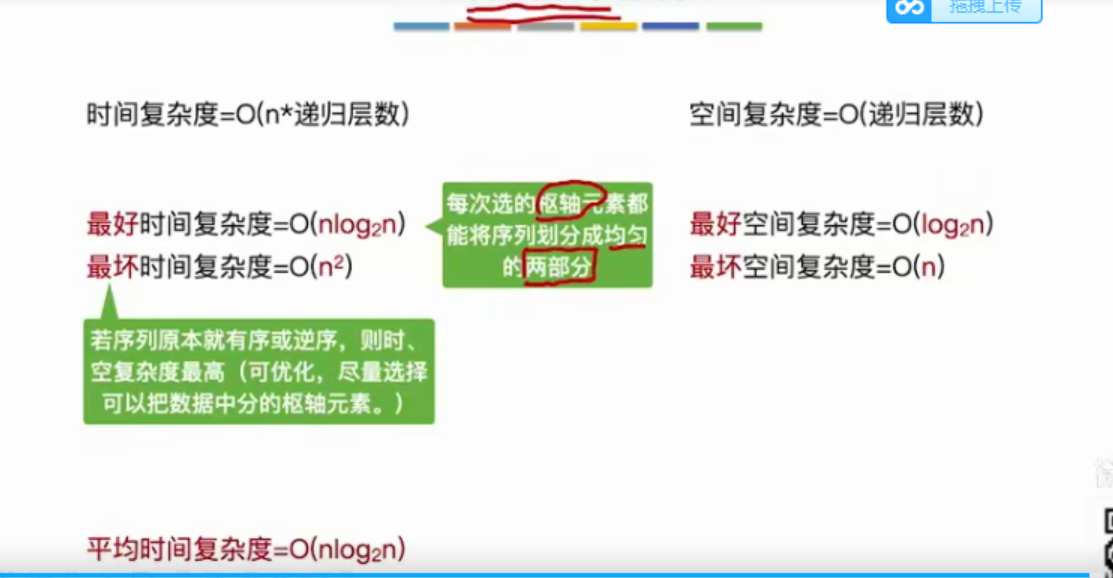
4.2.2 快速排序

//第一个元素将待排序序列划分为左右两个部分
int Partition(int A[],int low,int high){
    int pivot=A[low];
    while(low<high){
        while(low<high && A[high]>=pivot) --high;
        A[low]=A[high];
        while(low<high && A[low]<=pivot) ++low;
        A[high]=A[low];
    }
    A[low]=pivot;
    return low;
}
//快速排序
void QuickSort(int A[],int low,int high){
    if(low<high){
        int pivotpos=Partition(A,low,high);
        QuickSort(A,low,pivotpos-1);
        QuickSort(A,pivotpos+1,high);
}

快速排序是不稳定的

4.3 选择排序

4.3.1 简单选择排序

//适用于链表和顺序表s
void SelectSort(int A[],int n){
    for(int i=0;i<n-1;i++){
        int min=i;
        for(int j=i+1;j<n;j++)
            if(A[j]<A[min])
                min=j;
        if(min!=i)
            swap(A[i],A[min]);
    }
}

是不稳定的

4.3.2 堆排序

//建立大根堆
void BuildMaxHeap(int A[],int len){
    for(int i=len/2;i>0;i--){
        HeadAdjust(A,i,len);
    }
}
//将以K为根的子树调整为大根堆
void HeadAdjust(int A[],int k,int len){
    A[0]=A[k];
    for(int i=2*k;i<=len;i*=2){
        if(i<len && A[i]<A[i+1])
            i++;
        if(A[0]>=A[i]) break;
        else{
            A[k]=A[i];
            k=i;
        }
    }
    A[k]=A[0];
}

//基于大根堆进行排序（代码）
void BuildMaxHeap(int A[],int len);
//将以K为根的子树调整为大根堆
void HeadAdjust(int A[],int k,int len);
//堆排序的完整逻辑
void HeadSort(int A[],int len){
    BuildMaxHeap(A,len);
    for(int i=len;i>1;i--){
        swap(A[i],A[1]);
        HeadAdjust(A,1,i-1);
    }
}

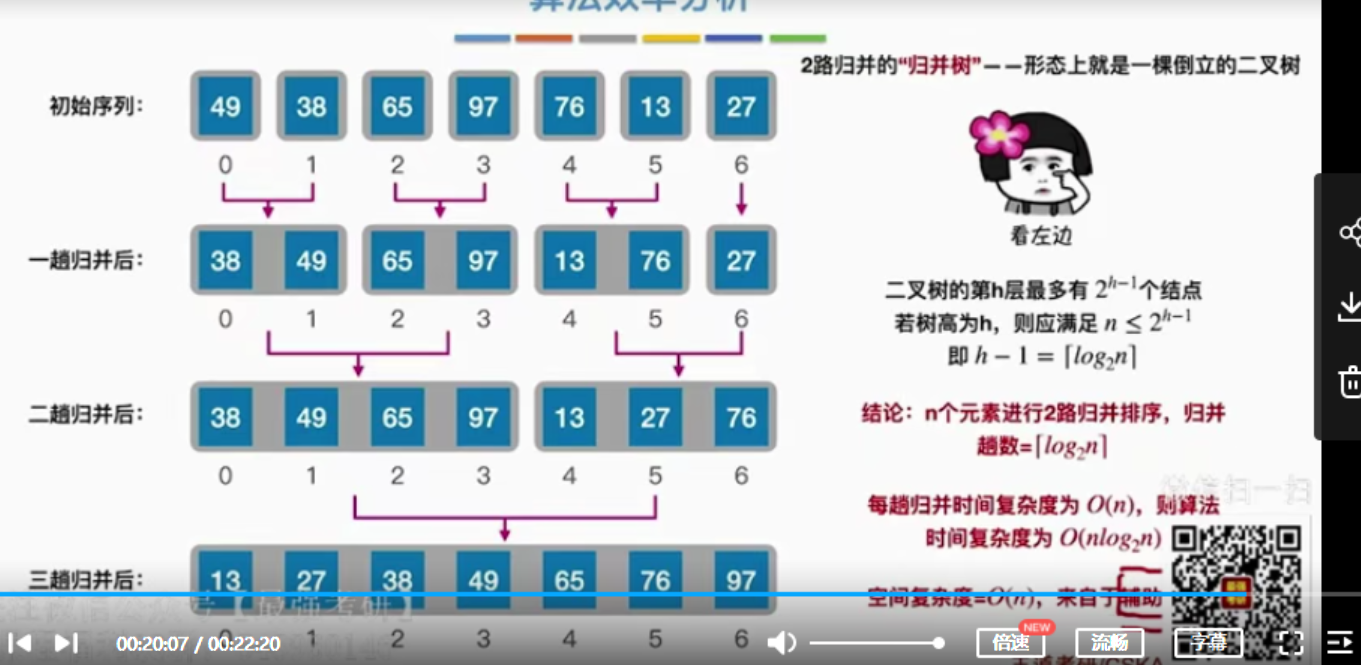
4.4 归并排序（Merge）

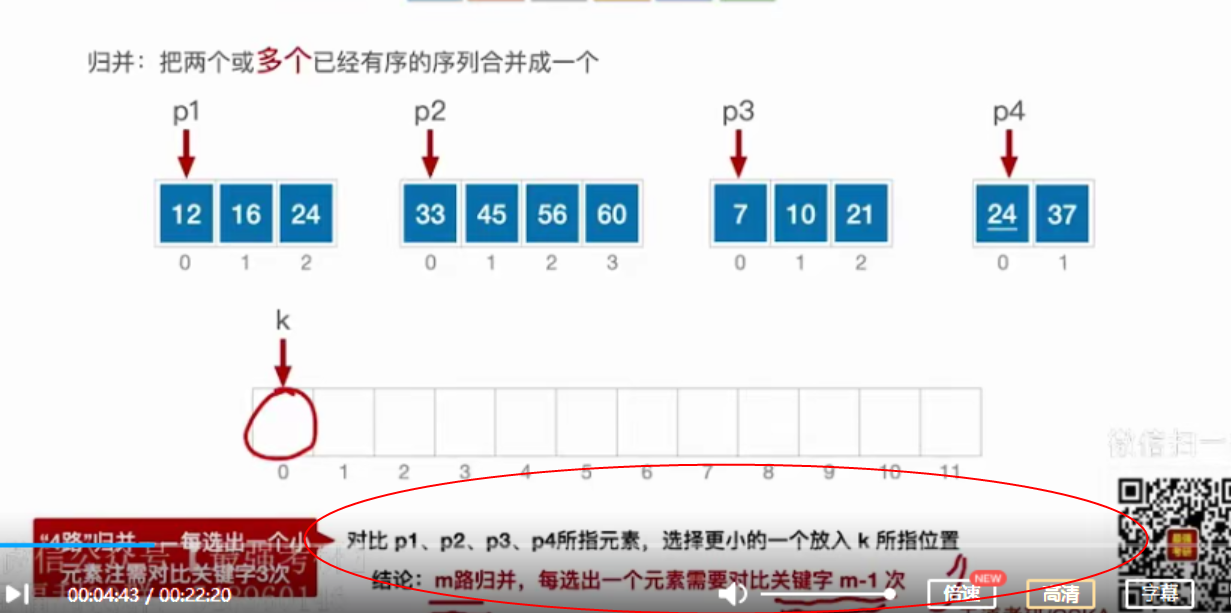
int *B=(int *)malloc(n*sizeof(int));
void Merge(int A[],int low,int mid,int high){
    int i,j,k;
    for(k=low;k<=high;k++)
        B[k]=A[k];
    for(i=low,j=mid+1,k=i;i<=mid && j<=high;k++){
        if(B[i]<=B[j])
            A[k]=B[i++];
        else
            A[k]=B[i++];
    }
    while(i<=mid) A[k++]=B[i++];
    while(j<=high) A[k++]=B[i++];
}
void MergeSort(int A[],int low,int high){
    if(low<high){
        int mid=(low+high)/2;
        sMergeSort(A,low,mid);
        MergeSort(A,mid+1,high);
        merge(A,low,mid,high);
    }
}

归并排序是稳定的

4.5 基数排序

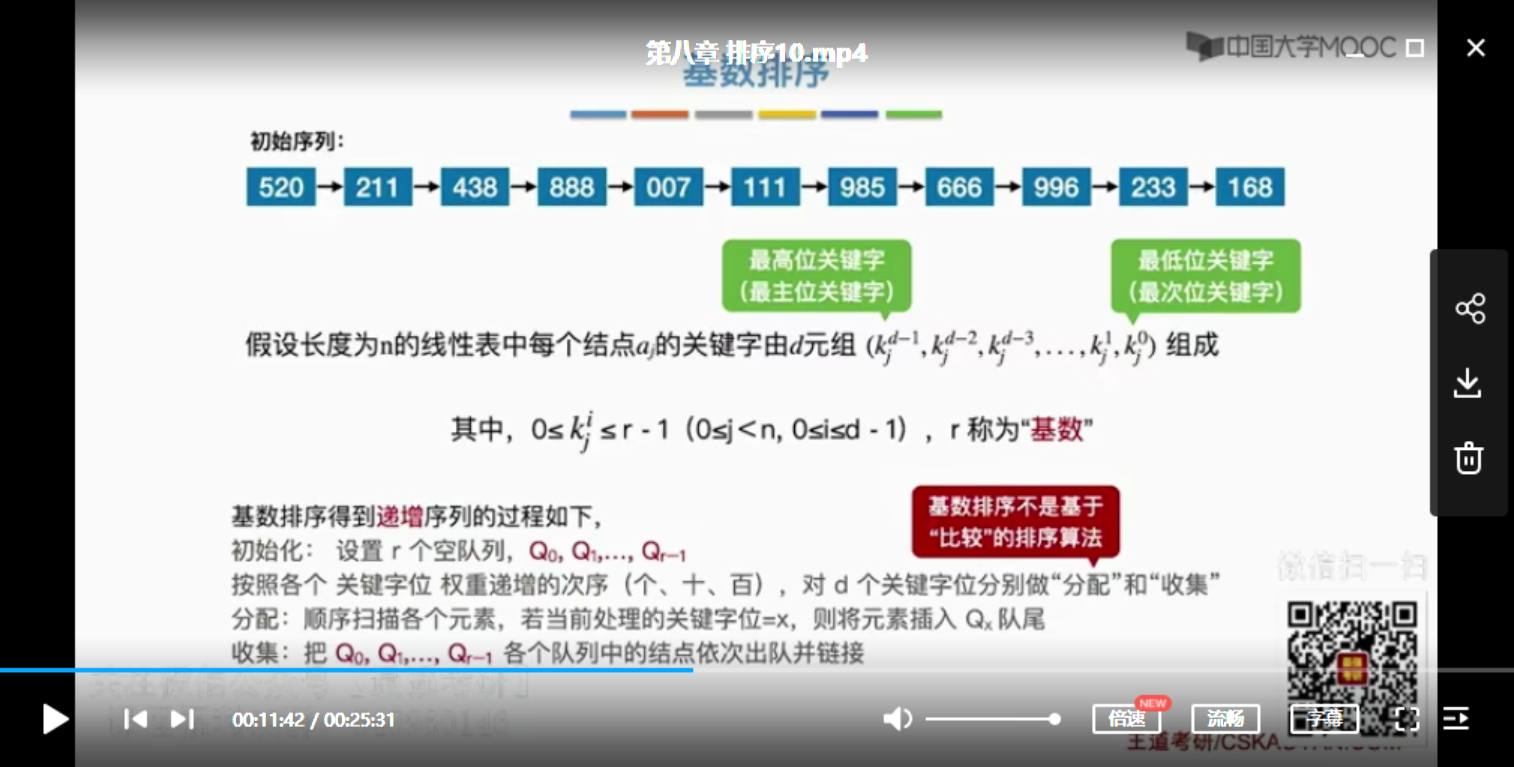
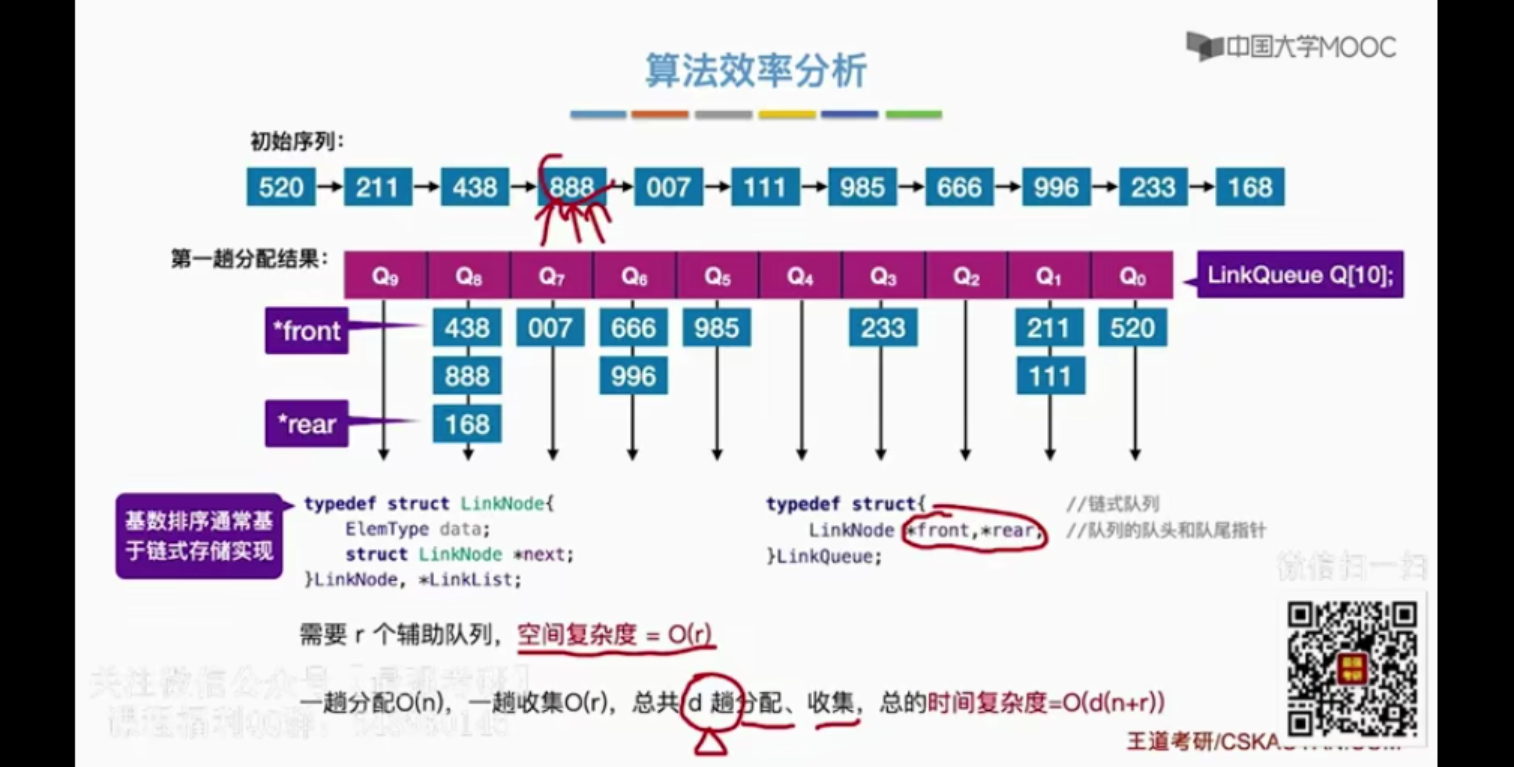
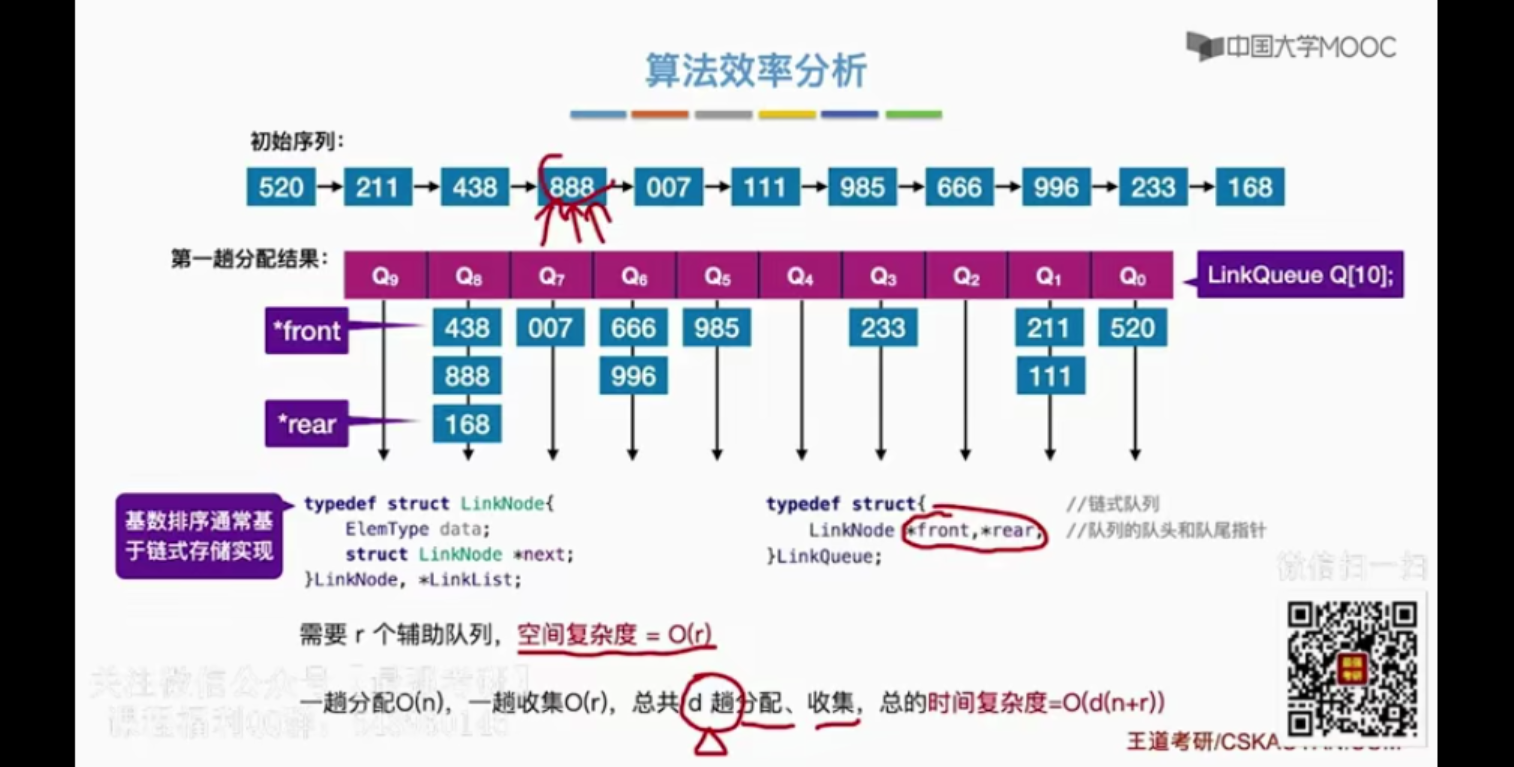
基数排序是稳定的