1.动态规划的定义
2.动态规划与分治的区别
2.动态规划的经典题目举例

动态规划的定义

动态规划（dynamic programming) 通过拆分问题，定义问题状态和状态之间的关系，使得问题能够以递推（或者说分治）的方式去解决。

动态规划的本质，是对问题状态的定义和状态转移方程的定义。

什么是状态转移？我们拿斐波那契数列来举个栗子！

  1. int fib(int n)  
  2. {  
  3.     if (n == 0 || n == 1)  
  4.     {  
  5.         return n;  
  6.     }  
  7.     else  
  8.     {  
  9.         return fib(n-1) + fib(n-2);  
  10.     }  
  11. }

这是一个简单的递归斐波那契数列，使用递归树来解决，时间复杂度是O(2^n)级别的（指数级增长的 ) ，如果n特别大的时候，其所占用的内存很大，运行的时间也很长。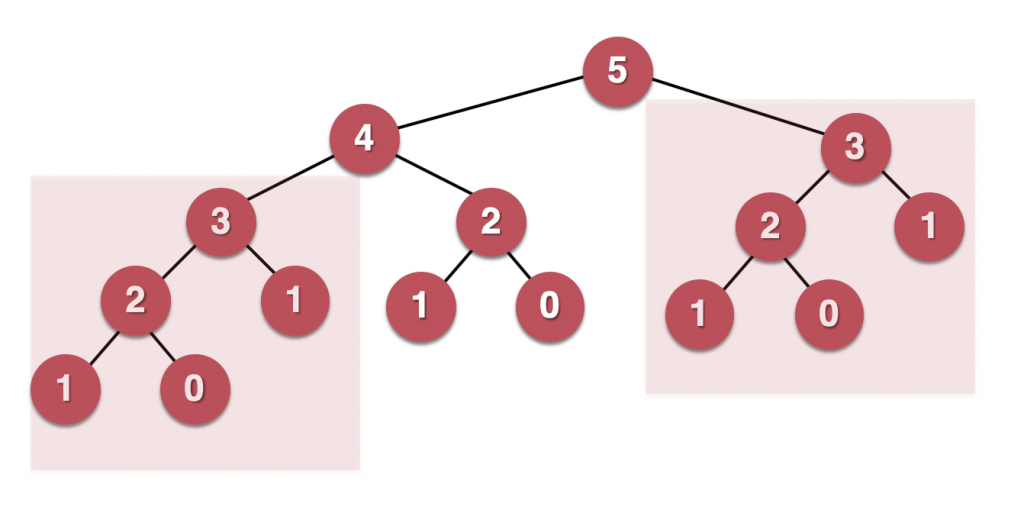
动态规划 - 图1
其原因是因为递归树中有很多重复的计算，这些计算并没有被利用起来，而是一次又一次的重复计算，这就造成了很大的时间空间的浪费。那么我们能不能想办法，把之前计算过的值（子问题）都记录下来，然后下次使用的时候，就直接拿来用，这样既可以节省大量的时间，又可以节省大量的空间，那么这种方法就叫做动态规划，而状态转移，就是把一些子问题记录下来，供其他动作调用。

我们先用记忆化搜索的方式，解决下斐波那契：

  1. vector<int> memo;
  2. int num = 0;int fib( int n ){
  3.     if( n == 0 )    
  4.         return 0; 
  5.     if( n == 1 )  
  6.         return 1; 
  7.     if( memo[n] == -1 ) 
  8.         memo[n] = fib(n-1) + fib(n-2);
  9.     return memo[n];
  10. }
  • 记忆化搜索使用数组memo[i]记忆第i个fib数列；
  • 对于每一个n来说，只会使用递归计算一次；
  • 记忆化搜索：在递归的基础上添加记忆化过程，自顶向下的解决问题。
    1. 1.与递归实现：100万倍的差距
    2. 2.记忆化搜索：在递归的基础上添加记忆
    3. 3.记忆化搜索实现fib的时间效率：O(n)
    那么使用动态规划的思路怎么解决呢？
    int fib( int n ){
  vector<int> memo(n+1, -1);
    memo[0] = 0;
    memo[1] = 1;
    for( int i = 2 ; i <= n ; i ++ )
      memo[i] = memo[i-1] + memo[i-2];
    return memo[n];
}
    动态规划：自底向上地解决问题；
    先解决小问题再解决大问题；
    动态规划实现fib的时间效率：O(n)。
    那么我们在回顾一下动态规划的概念：
    动态规划：将原问题拆解成若干子问题，同时保存子问题的答案，使得每个子问题只求解一次，最终获得原问题的答案。

    动态规划和分治的区别

    1.动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题,但是经分解得到的子问题往往不是互相独立的。不同子问题的数目常常只有多项式量级。在用分治法求解时，有些子问题被重复计算了许多次。
    2.如果能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，就可以避免大量重复计算，从而得到多项式时间算法。
    3.分治方法将问题划分为互不相交的子问题，递归地求解子问题，再将它们组合起来，求出原问题的解；
    4.动态规划应用于子问题重叠的情况，即不同的子问题具有公共的子子问题（子问题的求解是递归进行的，将其划分为更小的子子问题）。对每个子子问题只求解一次，将其解保存在一个表格中，从而无需每次求解一个子子问题时都重新计算。